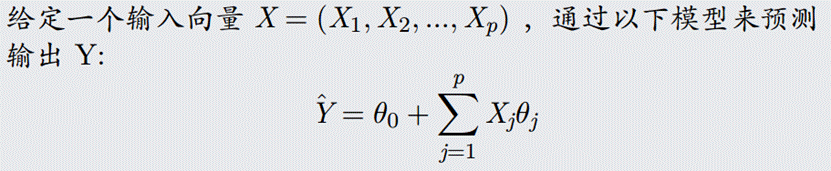深度学习(一)，线性回归与逻辑回归-Toy模板网

这篇具有很好参考价值的文章主要介绍了深度学习(一)，线性回归与逻辑回归。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

代码是自己敲得，图是自己画的，连公式都是一个一个字打的, 希望赞是你给的(≧◡≦)。

一，介绍

线性回归(Liner Regression),俗称lr。

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

一个大家熟悉得不能再熟悉的式子，便是线性回归的真身。其中a作为要学习的系数，b则是误差项。如果有多个变量，如

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

这便成为了多元线性回归。

这个模型吧很基础也很常见，不管你是学统计学还是机器学习还是深度学习，第一个了解的模型应该都是它。也就是说，lr既可以算作一种统计模型,也能算作一种机器学习模型，但我觉得很多人不知道的是，它其实也能算作一种深度学习模型。如果你熟悉神经网络的话，就会发现，线性回归不就是只有一层且output 为1的神经网络吗，这一点在后面了解了神经网络之后应该会有更深的体会。

接下来我将仔细的讲解一下线性回归，希望大家看完能有更深的了解。

二，最小二乘法的线性回归

以一元线性回归为例，假设我们有以下数据：

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

左边是我随手敲的一些数据，从肉眼来看，自变量X与因变量Y之间是存在着线性相关性的,即X变大,Y也变大。于是我们希望用一条直线，来代表他们之间的这种线性相关性（也就是说如果想使用线性回归来拟合数据，请确保与拟合的响应变量/因变量之间是具有线性相关的.）。用方程来表示一条直线，也就是我们从高中就很熟悉的 y = ax+b。暂时先假设我们想要找的那一条直线就是这个(在右图中表现为那一条虚线)

方程设好了之后，接下来的问题就是如何调整该方程的参数a和b,使其能够更好的体现我们现有数据里面的线性趋势。那么就引申出了两个问题：

怎么样去判断我们的这条直线有没有很好的代表数据里面的线性趋势？如何量化成一个具体的数值？(损失函数)
假设我们现在知道了我们的直线没有很好的代表数据里面的线性趋势，并且差得很远，我们该如何优化参数a和b,使我们的直线表现得更好？(求导)

2.1 损失函数

对于当前直线所代表的线性趋势与数据集里面的线性趋势的差距，我们用损失函数来衡量。损失函数的种类多种多样，而最小二乘法使用的则是十分经典的均方误差(MSE)作为损失函数即(每一个预测值 — 对应实际值)的平方的简单平均. 我们用如下公式来表达：(也有的会把1/n直接省略掉，不过都是一样的对结果没有影响),

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

这是一个二元函数，其中系数a和误差项b是未知变量，而xi,Yi都是已知的.(Yi是我们数据中的每一个实际值，因变量/响应变量,xi是每一个实际的自变量/解释变量)

这样，通过计算这个值，我们就得以衡量我们所假设的直线与所代表的线性趋势与实际的线性趋势之间的差距。

2.2 求解析解

现在到了第二个问题，如何优化参数a,b，让我们的直线离真实的线性趋势更加靠近呢？既然有了E(a,b)值作为度量，那我们只需要使它最小化就可以了。而通过微积分我们可以知道，对于多元函数，对每个自变量求偏导并使其为0，就是它的极值点。

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

这样，我们就得到了两个方程，剩下的就是解开这个方程组就可以得到a与b的具体值了。也就是说，最小二乘法的线性回归的参数是可以得到最小平方误差意义下的解析解的，可以直接算出来。这也是唯一一个有解析解的模型了，且算且珍惜。

当然我们一般不会去解这个方程组，更加方便的做法是利用线代的知识，给它们写成矩阵的形式。

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

再此基础上，我们可以进一步简化, 矩阵可以进一步简化为:

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

这应该也是很多人见过最多的形式，写成这种形式，不仅有助于理解，我们用代码实现起来也会方便很多，直接用numpy建立array进行相应的矩阵运算就可以了。但很多人没有把额外的那一列1，列出来，而是直接给了最终的式子，导致很多人会漏掉这一列，从而出现了理解上的误差。这一列的作用其实就是用来拟合b,拟合误差项的。

2.3 代码实现

以上面给出的具体数值为例,实现起来真的很简单。

import numpy as np
from matplotlib import pyplot as plt

def LR(matrix_X, matrix_Y):                 
    '''
    定义最小二乘法的线性回归模型
    '''
    weight = np.dot(matrix_X.T, matrix_X)
    weight = np.linalg.inv(weight)
    weight = np.dot(weight, matrix_X.T)
    weight = np.dot(weight, matrix_Y)
    predict = np.dot(matrix_X, weight)
    return weight, predict

def r_squared(predict, actual):
    """
    计算并返回R^2值。
    """
    # 计算残差平方和SS_res
    ss_res = np.sum((actual - predict) ** 2)
    # 计算总平方和SS_tot
    ss_tot = np.sum((actual - np.mean(actual)) ** 2)
    # 计算R^2值
    r2 = 1 - ss_res / ss_tot
    return r2

# 准备数据
matrix_X = np.array([ [1,1],
                      [2,1],
                      [3,1],
                      [4,1],
                      [5,1]])
matrix_Y = np.array([4,8,7,9,12]).T

# 得到预测结果及系数矩阵
weight,predict = LR(matrix_X, matrix_Y)

深度学习(一)，线性回归与逻辑回归,线性回归,逻辑回归,算法,机器学习,人工智能,深度学习

从图像上来看的话，效果也还是不错的.文章来源地址https://www.toymoban.com/news/detail-843268.html

2.4 效果评估

def r_squared(predict, actual):
    """
    计算并返回R^2值。
    """
    # 计算残差平方和SS_res
    ss_res = np.sum((actual - predict) ** 2)
    # 计算总平方和SS_tot
    ss_tot = np.sum((actual - np.mean(actual)) ** 2)
    # 计算R^2值
    r2 = 1 - ss_res / ss_tot
    return r2


# 效果评估,这里我们用经典的R^2值来评估.它介于0~1之间，越大说明拟合效果越好

##(R^2 > 0.9)：通常表示模型具有非常好的拟合效果，能够解释大部分的数据变异性。
##(0.7 < R^2 < 0.9)：通常表示模型有较好的拟合效果，能够解释相当一部分数据变异性。
##(0.5 < R^2 < 0.7)：表示模型的拟合效果一般，只能解释一半左右的数据变异性。
##(R^2 < 0.5)：通常意味着模型的拟合效果不佳，无法解释大部分数据的变异性。

R2 = r_squared(predict, matrix_Y) 
#我这里计算出来为0.85，说明效果不错，因为数据集本身线性相关性就很明显