C代码快速傅里叶变换-分类和推理-常微分和偏微分方程-Toy模板网

这篇具有很好参考价值的文章主要介绍了C代码快速傅里叶变换-分类和推理-常微分和偏微分方程。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

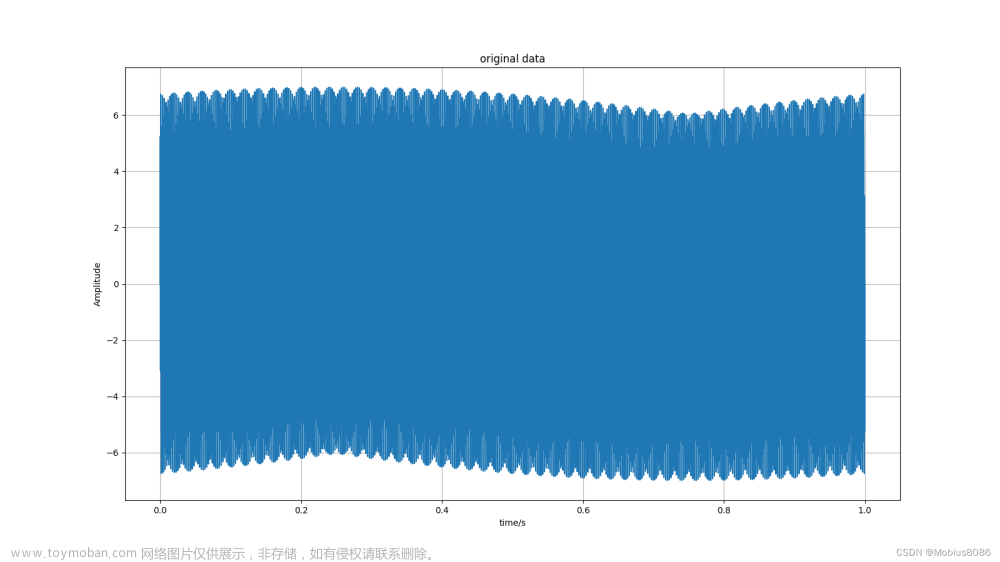
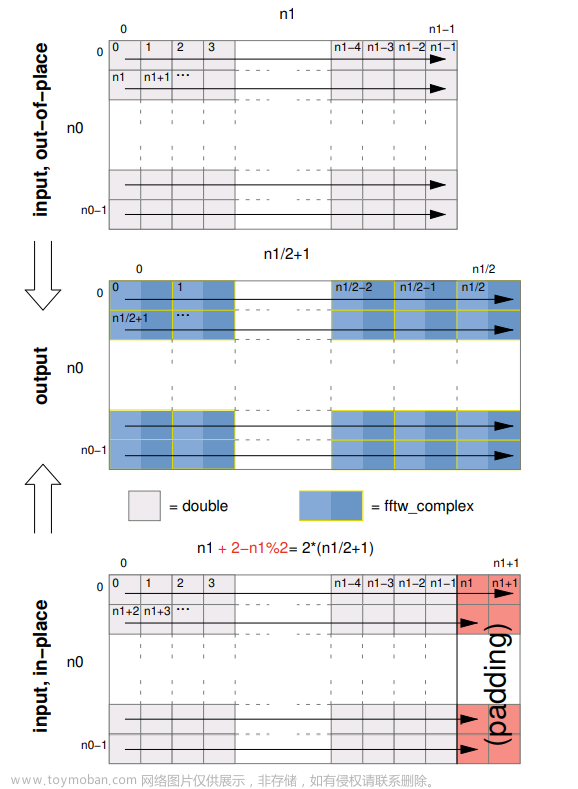
要点

C代码例程函数计算实现：
1. 线性代数方程解：全旋转高斯-乔丹消元，LU分解前向替换和后向替换，对角矩阵处理，任意矩阵奇异值分解，稀疏线性系统循环三对角系统解，将矩阵从完整存储模式转换为行索引稀疏存储模式，稀疏系统的共轭梯度法，范德蒙矩阵，托普利茨矩阵，QR分解。
2. 插值和外推：多项式，有理函数，三次样条，插值多项式的系数，双三次插值。
3. 数值积分：龙伯格积分，第二个欧拉-麦克劳林求和，高斯求积和正交多项式，高斯-埃尔米特求积，高斯-雅可比求积，一元正交多项式。
4. 评估函数：欧拉变换，加速序列收敛，连续分数的综合除法多项式，Ridders 多项式外推法，切比雪夫多项式，切比雪夫系数多项式近似，帕德近似值，有理切比雪夫近似。
5. 特殊函数：对数伽马函数，指数积分，使用连续分数评估计算贝塔函数，整数阶贝塞尔函数，艾里函数，球面贝塞尔函数，球谐函数，菲涅尔积分，余弦和正弦积分，道森积分，椭圆积分和雅可比椭圆函数
6. 随机数：最高质量随机数生成，高质量哈希值生成，滞后斐波那契生成器，生成指数偏差和逻辑偏差，Box-Muller 变换（正态偏差），柯西偏差，均匀比方法，伽玛偏差，泊松偏差，二项式偏差，多元正态偏差，蒙特卡洛积分应用，索博尔序列，VEGAS算法。
7. 非线性方程集，最小最大函数，快速傅里叶变换，统计数据描述，数据模型，分类和推理，常微分方程积分，两点边界值问题，积分方程和反演理论，偏微分方程，计算几何，算法。

C/C++代码蒙特卡洛积分示例

对于光子学、经济学、视频游戏开发和工程学等许多依赖数值的领域来说，求解复杂积分是必需的。
$I=\int_a^b g(x) d x$
许多有趣的问题都无法通过分析求解积分，因此必须应用替代数值方法来找到适当的估计。值得注意的是，通过应用数值方法（例如蒙特卡洛积分），我们并不是“求解”积分，而是对积分值进行适当的估计。对于许多应用来说，这种差异可以忽略不计，但应牢记这种区别，特别是在考虑当前问题所需的准确度时。

“蒙特卡洛方法”的现代变体可以追溯到 20 世纪 40 年代的洛斯阿拉莫斯实验室，该实验室最初开发该方法是为了帮助模拟核裂变过程，特别是模拟裂变材料中中子的平均自由程。我们没有确定地解决中子的扩散路径，而是应用了统计采样方法，而且效果非常好。从那时起，“蒙特卡罗方法”一词根据其应用领域的不同而具有广泛的含义。然而，蒙特卡罗的所有应用都有一个共同的基本原理，即使用统计采样来解决确定性难以解决的问题。

蒙特卡罗积分器

首先，我们可以使用蒙特卡罗检查积分的期望值。传统上，函数 g(x) 的期望值可以通过首先乘以其概率密度函数 f(x)，然后在所需区域上进行积分来计算：
$E[g(x)]=\int_a^b g(x) f(x) d x$
或者，我们可以通过对积分极限之间的均匀分布重复采样来使用蒙特卡罗近似来获得期望值。
$E[g(x)]=\frac{1}{n} \sum_{i=1}^n f\left(x_i\right)$
其中， $x_i \in[a, b]$ 。

如前所述， $x i$ 是从每个唯一 $n = 1, 2, 3$ 等的限制 $a$ 和 $b$ 之间的均匀分布中采样的值。这种方法对 $f (x) 进行采样$ 函数并使用大数定律来找到收敛的期望值。

乘法因子 $1/ n$ 有时给出为 $1/ (n - 1)$ 因为 $n$ 个样本确实有 $n - 1$ 个自由度，但是当 $n$ 很大时 $1/ n$ 和 $1/ (n - 1)$ 之间的差异可以忽略不计。给定期望值估计量的形式，扩展到积分的估计很简单。期望值公式乘以积分限制的范围，如下所示。
$\frac{1}{n} \sum_{i=1}^n f\left(x_i\right)$
其中， $x_i \in[a, b]$ 。

积分估计使用期望值估计器以及由积分限制确定的矩形宽度来查找积分面积/体积的近似值。我们可以用一个相对简单的例子来测试它，取积分：
$\int_1^5 x^4 e^{-x} d x$
我们可以编写一个简短的 C++ 程序来应用蒙特卡罗积分技术，样本大小为 n = 200。

#include <iostream>
#include <cstdlib>
#include <cmath>

double myFunction(double x);
double monteCarloEstimate(double lowBound, double upBound, int iterations);

int main()
{

	double lowerBound, upperBound;
	int iterations;

	lowerBound = 1;
	upperBound = 5;
	iterations = 200;

	double estimate = monteCarloEstimate(lowerBound, upperBound,iterations);

	printf("Estimate for %.1f -> %.1f is %.2f, (%i iterations)\n",
			lowerBound, upperBound, estimate, iterations);

	return 0;
}


double myFunction(double x)
//Function to integrate
{
	return pow(x,4)*exp(-x);
}

double monteCarloEstimate(double lowBound, double upBound, int iterations)
{

	double totalSum = 0;
	double randNum, functionVal;

	int iter = 0;

	while (iter<iterations-1)
	{

		randNum = lowBound + (float(rand())/RAND_MAX) * (upBound-lowBound);
		functionVal = myFunction(randNum);
		totalSum += functionVal;

		iter++;
	}

	double estimate = (upBound-lowBound)*totalSum/iterations;

	return estimate;
}

它应该打印一些接近于：

Estimate for 1.0 -> 5.0 is 13.28, (200 iterations)

我们必须考虑蒙特卡罗积分技术隐含的方差。蒙特卡罗积分方案的方差遵循计算某个随机变量方差的传统过程。如果我们继续前面对函数 $g (x)$ 求积分的表示法，则 $g (x)$ 积分期望值的方差可以给出。为了简洁起见，我将跳过蒙特卡罗积分方案固有的标准差关系的推导。如果我们继续采用对函数 $g (x)$ 进行积分的表示法，并且积分的期望值为 $E [g (x)]$ ，则标准差的关系可以给出为：
$\sigma_n=V \sqrt{\frac{E\left[g(x)^2\right]-E[g(x)]^2}{n-1}}$ 文章来源地址https://www.toymoban.com/news/detail-843296.html