今天又是补打卡的一天,开冲!!!
今日任务:
- 70.爬楼梯(进阶)
- 322.零钱兑换
- 279.完全平方数
题目一:爬楼梯(进阶)
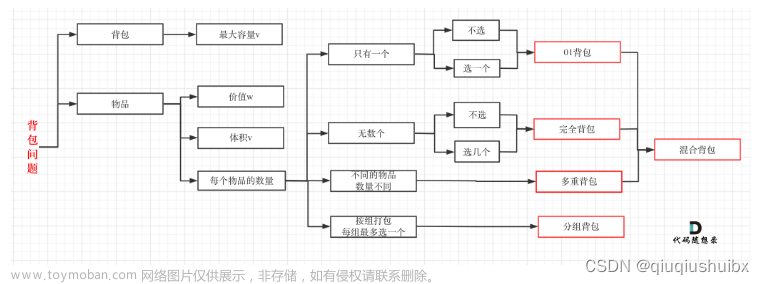
这道题之前做过一次,但是可以采用完全背包的问题来分析一遍。
卡玛网题目:【57.爬楼梯】

这个题目其实是更难了一点,因为前面的题目都是每次要不爬1阶楼梯,要不爬2阶楼梯,现在相当于是任选,而且还是可以重复利用的,因此此问题可以转化为排列方式的完全背包问题。
按照递归五部曲:
(1)定义dp数组及其含义:
dp[j]表示爬到j阶楼梯,有dp[j]种方法。
(2)确定递推公式:
因为这个是方法类的,所以递推公式通常为:dp[j] = dp[j-nums[i]],此题种的nums[i]对应的就是1、2、3、4这种,因此可以转换为dp[j] = dp[j-i];
(3)dp数组初始化:
dp[0] = 1;如果初始化dp[0] = 0,那后面的全部都是0;
(4)确定遍历顺序:
因为这个是排列的完全背包问题;
完全背包问题相对于01背包问题,其实是第二层变成了从左到右遍历,然后因为又是排列的问题,所以是先背包后物品。
(5)打印dp数组:
一般用来判断和自己想的是否一致
易错点:在递推公式前面需要判断一下才能放,这个是完全背包排列问题中非常重要的东西
#include <iostream>
#include <vector>
using namespace std;
int main(){
int m = 0, n = 0;
while(cin >> n >> m){
vector<int> dp(n+1);
dp[0] = 1;
for(int i = 1; i<=n; i++){
for(int j = 0; j<=m; j++){
if(i>=j) dp[i] += dp[i-j];
}
}
cout << dp[n];
}
return 0;
}
题目二:零钱兑换
Leetcode题目:【322.零钱兑换】

从题目中大致可以看出来是完全背包类的题目,按照递归五部曲:
1、定义dp数组的含义:dp[j]表示装满j,最少的硬币数目为dp[j];
2、确定递推公式:
dp[j] = min(dp[j-coins[i]] + 1, dp[j]);
3、初始化:
dp[0] = 0;
因为取得都是最小,故为了不影响式子的值,所以需要初始化最大值;
4、遍历顺序:
按照完全背包的问题,可以是组合也可以是排列问题;
5、打印dp数组
此处需要注意在递推公式的判断条件,因为有可能dp[i]某些并不会初始化。
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for(int i = 0; i<coins.size(); i++){
for(int j = coins[i]; j<=amount; j++){
//dp[j] = min(dp[j], dp[j-coins[i]] + 1);
if (dp[j - coins[i]] != INT_MAX){
dp[j] = min(dp[j], dp[j-coins[i]] + 1);
}
}
}
if (dp[amount] == INT_MAX) return -1;
for(int i = 0; i<=amount; i++){
cout << dp[i] << " ";
}
return dp[amount];
}
};
题目三:279.完全平方数
Leetcode题目:【279.完全平方数】

这个题跟上面的题目基本一样,只不过此题需要我们自己去创造物品,物品就是i*i,因为完全平方数中存在1,所以不可能存在不能拼凑的情况。文章来源:https://www.toymoban.com/news/detail-843300.html
按照递归五部曲:
(1)确定dp数组含义:dp[j]表示装满数量为j的背包,需要的最少完全平方数的个数;
(2)确定递推公式:
dp[j] = dp[j-nums[i]] + 1 变为dp[j] = dp[j-ii] + 1,因为是求最小,所以
dp[j] = min(dp[j], dp[j-ii] + 1);
(3)初始化:dp[0] = 0,同时其他设置为最大值INT_MAX;
(4)确定遍历顺序:
因为此题是完全背包问题,所以都是正序,因为是组合问题,所以可以先物品再背包;
(5)打印dp数组;文章来源地址https://www.toymoban.com/news/detail-843300.html
class Solution {
public:
int numSquares(int n) {
// 题目就是自己去构造物品
vector<int> dp(n+1, INT_MAX);
dp[0] = 0;
for(int i = 1; i*i <= n; i++){
for(int j = i*i; j<=n; j++){
if(dp[j-i*i] != INT_MAX){
dp[j] = min(dp[j], dp[j-i*i] + 1);
}
}
}
return dp[n];
}
};
到了这里,关于【Day45】代码随想录之动态规划part7—爬楼梯(进阶)、零钱兑换、完全平方数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!