5.岛屿的最大面积
- 题目描述
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。
示例 1：
文章来源：https://www.toymoban.com/news/detail-843310.html
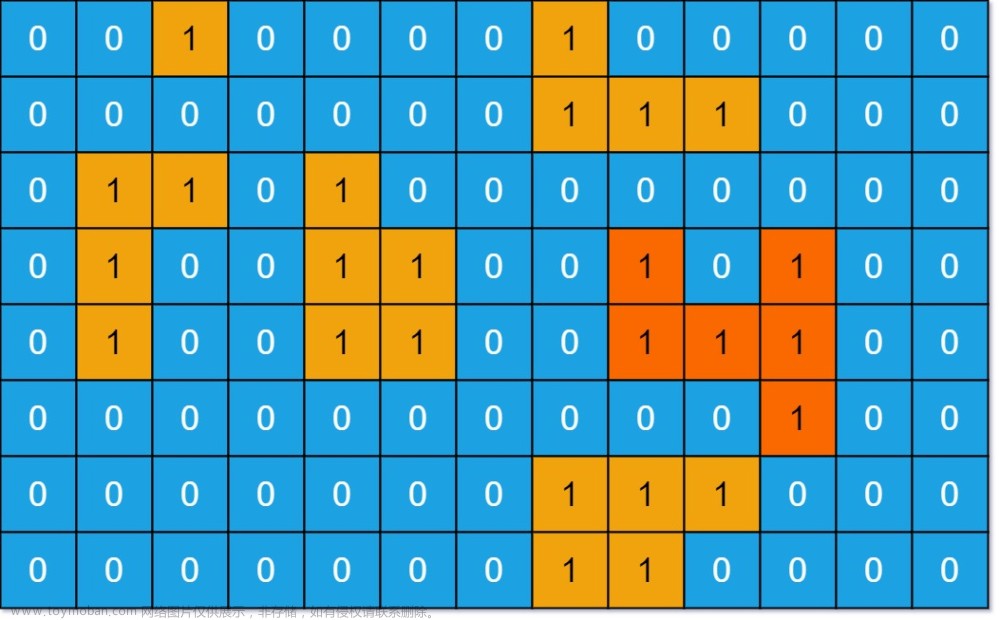
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2：文章来源地址https://www.toymoban.com/news/detail-843310.html
输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0
- 题目分析
1.题目要求计算给定二进制矩阵 grid 中最大的岛屿面积，其中岛屿由相邻的1构成，相邻的1必须在水平或竖直方向上相邻。可以假设矩阵边缘被0包围。
2.思路分析
--遍历整个二维矩阵 grid，对每个位置进行如下操作：
--如果当前位置为1，则进行深度优先搜索（DFS）来计算当前岛屿的面积。
--在DFS过程中，将访问过的位置标记为0，并累加岛屿的面积。
--维护一个变量 maxArea 来记录遍历过程中出现的最大岛屿面积，不断更新这个值。
--最终返回 maxArea 即为最大的岛屿面积。
3.代码分析
全局变量定义：
max：记录最大岛屿面积。
spare：记录当前岛屿的面积。
maxAreaOfIsland 方法：
遍历整个二维数组 grid，对每个位置进行如下操作：
如果当前位置为1，表示发现一个新的岛屿，调用 dfs 方法计算当前岛屿的面积。
更新 max 为当前最大值，并将 spare（当前岛屿面积）置零。
返回最大岛屿面积 max。
dfs 方法：
深度优先搜索方法，用于计算岛屿的面积。
判断当前位置是否越界，如果越界则返回。
如果当前位置为0，表示没有岛屿，直接返回。
若当前位置为1，增加当前岛屿面积 spare，并将当前位置标记为0，避免重复计算。
递归调用DFS，向上、下、左、右四个方向继续搜索岛屿。
复杂度分析：
时间复杂度：O(m*n)，m 和 n 分别为矩阵的行数和列数，需要遍历整个矩阵。
空间复杂度：O(1)，除了函数调用栈外，没有使用额外空间。
- Java代码实现
class Solution {
int max = 0;// 岛屿最大面积
int spare = 0;// 当前岛屿的面积
public int maxAreaOfIsland(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {// 表示如果岛屿存在
dfs(grid, i, j);// 获得一块岛屿的面积
max = Integer.max(max, spare);
spare = 0;
}
}
}
return max;
}
// 深度优先遍历的方法
private void dfs(int[][] grid, int i, int j) {
if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length) {
return;// 判断所处位置是否越界
}
if (grid[i][j] == 0) {
return;// 当前位置是否存在岛屿
}
spare++;// 表明岛屿存在，面积扩大
grid[i][j] = 0;// 防止重复计算
dfs(grid, i + 1, j);// 下
dfs(grid, i - 1, j);// 上
dfs(grid, i, j + 1);// 右
dfs(grid, i, j - 1);// 左
}
}
到了这里，关于图论05-岛屿的最大面积(Java)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
