图论02-并查集的实现(Java)-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论02-并查集的实现(Java)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

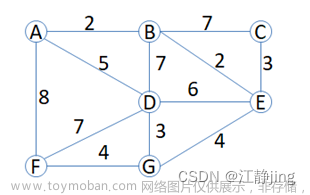
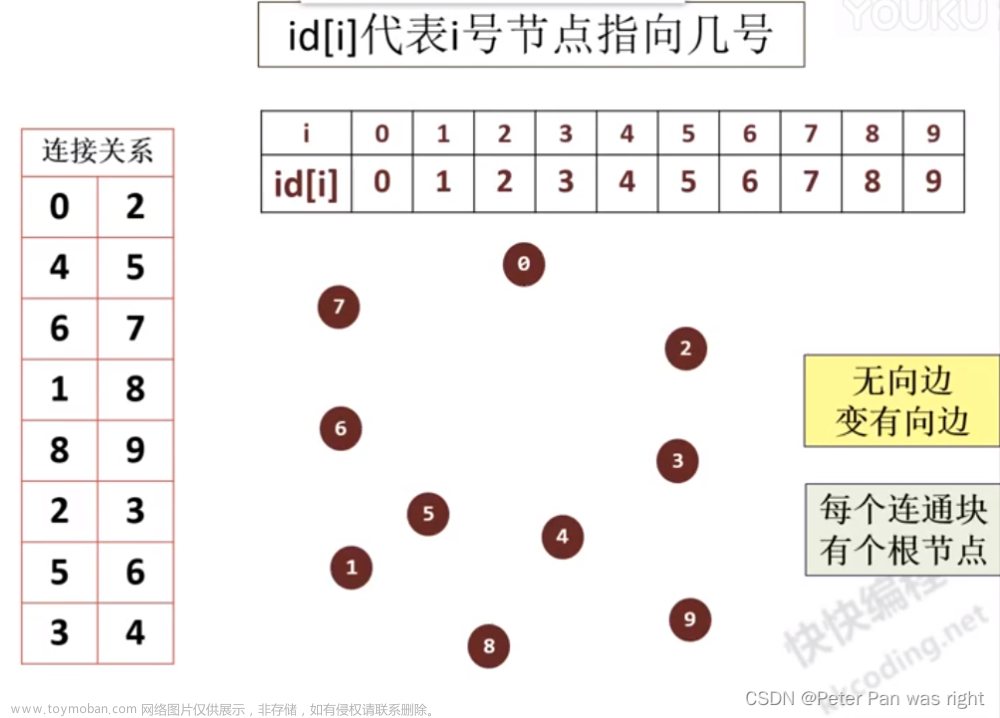
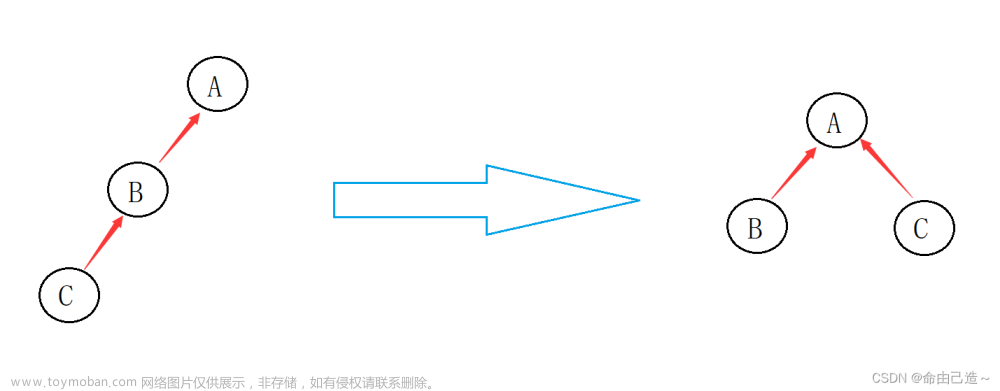
2.并查集理论基础

并查集的作用

将两个元素添加到一个集合中。
判断两个元素在不在同一个集合

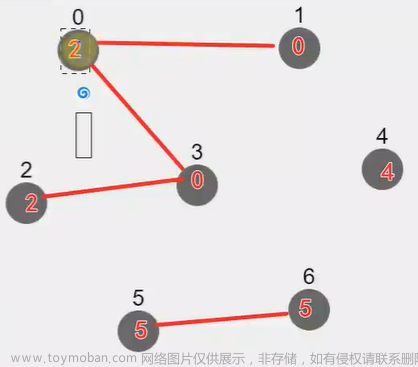
并查集的实现

图论02-并查集的实现(Java),算法学习,图论,java

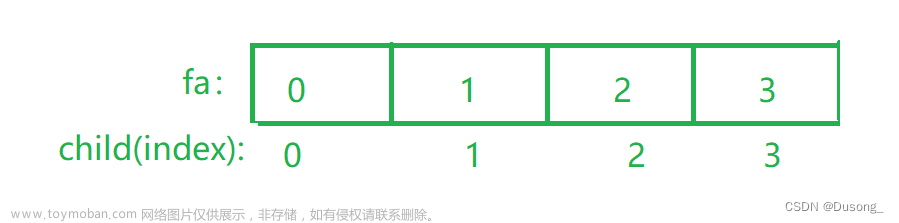
1.DSU 类定义：DSU 类中包含一个整型数组 s 用来存储元素的父节点信息。

2.DSU 构造函数：
构造函数 DSU(int size) 接受一个参数 size，初始化了大小为 size 的并查集。
在构造函数中，数组 s 被初始化为一个大小为 size 的数组，初始时每个节点的父节点是自己。
find 方法：

3.find(int x) 方法用于查找元素 x 所在集合的根节点（即代表元素）。
如果 x 的父节点等于自己，则说明 x 就是根节点，直接返回 x。
否则递归调用 find 方法，找到 x 的父节点的根节点并返回。

4.union 方法：
union(int x, int y) 方法用于合并元素 x 和元素 y 所在的两个集合。
在该实现中，直接将 x 的父节点设置为 y，即将 x 所在集合的根节点指向 y 所在集合的根节点。

Java代码实现文章来源地址https://www.toymoban.com/news/detail-843360.html

public class DSU {
    int[] s;

    /**
     * 初始化并查集，指定大小，并将每个元素初始化为自己的父节点。
     * @param size 并查集的大小。
     */
    public DSU(int size) {
        s = new int[size];
        for (int i = 0; i < s.length; i++) {
            s[i] = i;
        }
    }

    /**
     * 查找操作，用于查找包含元素 x 的集合的根/父节点。
     * @param x 要查找的元素。
     * @return 包含 x 的集合的根节点。
     */
    public int find(int x) {
        if (x == s[x]) {
            return x;
        }
        return find(s[x]);
    }

    /**
     * 合并操作，用于合并包含元素 x 和 y 的集合。
     * @param x 第一个元素。
     * @param y 第二个元素。
     */
    public void union(int x, int y) {
        s[x] = y;
    }
}

x = set.find(2);//找2节点的代表节点
y = set.find(3);//找3节点的代表节点
if (x != y) {//当二者没有相同的代表节点表明二者不在同一个集合之中，可以连接
	set.union(x, y);
}

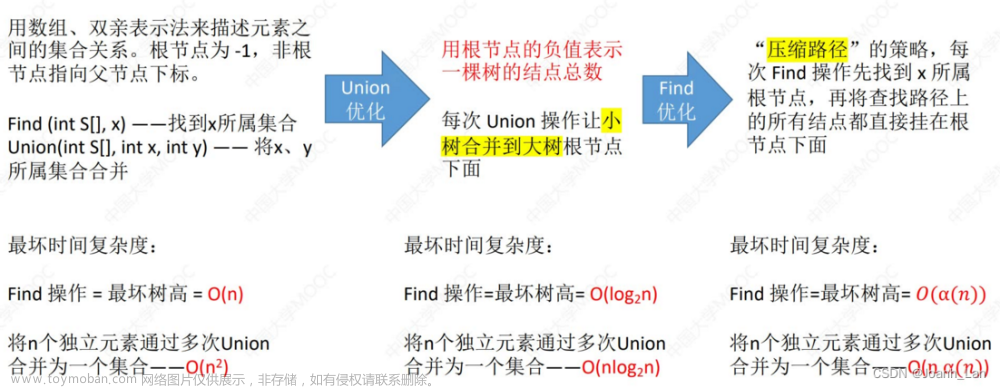
路径压缩

原因：在普通的并查集中，通过不断向上查找父节点的方式找到根节点，这可能导致树的深度较大，从而影响查找操作的效率。路径压缩通过在查找时将节点直接连接到根节点，减少了树的深度，提高了查找操作的效率。

方法：我们可以在查找父节点的时候，我们通过向上查找便可以知道谁是自己的父节点，相比直接返回父节点，我们可以顺便将自己指向父节点，这样可以降低树的深度
public int find(int x) {
        if (x == s[x]) {
            return x;
        }
        return s[x] = find(s[x]);
    }

优化后完整代码

DSU(int size) 构造函数：初始化并查集，创建了两个数组 s 和 size，分别用来存储集合中各点的关系和判断不同集合的大小。在初始化过程中，将每个节点的值初始化为索引的值，表示每个节点最初都是一个独立的集合，大小为1。

find(int x) 方法：查找元素 x 的根节点。通过递归地查找 x 的父节点，直到找到根节点为止。在查找的过程中，进行路径压缩操作，将沿途经过的节点直接指向根节点，从而降低树的深度，优化后续查找操作的效率。

union(int x, int y) 方法：合并两个集合。在合并操作中，首先根据两个集合的大小判断，让元素较少的集合指向元素较多的集合，以减小树的深度。然后更新集合的大小信息，确保合并后大集合的大小正确反映合并前两个集合的大小之和。

public class DSU {
    int[] s;//用来存储集合中各点的关系
    int[] size;//用来判断不同集合的大小

    public DSU(int size) {//初始化并查集
        s = new int[size];
        this.size = new int[size];
        for (int i = 0; i < s.length; i++) {
            s[i] = i;//将每个节点的值初始化为索引的值
            this.size[i] = 1;//此时每个索引代表一个集合，因此集合数目为1
        }
    }

    public int find(int x) {//查找元素x的根节点
        if (x == s[x]) {//如果节点的索引与节点的值一样，说明找到节点
            return x;
        }
        //如果不相等，根据值去找根节点，因为值记录的是根节点的位置
        //路径压缩：寻找根节点的难度会随着树的深度而不断增大，所以若找到根节点，直接将根节点的值赋值给x索引的值，从而降低树的深度
        return s[x] = find(s[x]);
    }

    public void union(int x, int y) {//合并两个集合
        //在进行查找根节点的时候，会从一个节点的值不断寻找
        //对于一个集合数目大的元素，查找起来更加费时，如果
        //让大的集合指向小的集合，会使树的深度再次增加，加大
        //复杂度，因此我们需要判断连个集合的大小，让小集合指向大集合
        if (size[x] < size[y]) {//判断集合的大小
            int temp = y;
            y = x;
            x = temp;
        }
        //x表示大集合，y表示小集合
        s[y] = x;//y集合的父节点为x
        size[x] = size[x] + size[y];//此时大集合的大小为原大集合的大小加小集合的大小
    }

    @Override
    public String toString() {
        return Arrays.toString(s);
    }
}