曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)

0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 什么是Reeds-Shepp曲线？

Reeds-Shepp曲线是一种用于描述在平面上从一个点到另一个点最优路径的数学模型。这种曲线是由美国数学家 J. A. Reeds 和 L. A. Shepp 在1990年提出的，它被广泛应用于路径规划和运动规划问题中。Reeds-Shepp曲线的很多原理和Dubins曲线类似，可以先学习曲线生成 | 图解Dubins曲线生成原理(附ROS C++/Python/Matlab仿真)

Reeds-Shepp曲线具有以下特点：

• 最优性：Reeds-Shepp曲线是连接两个点的最短路径之一，通常是沿着曲线长度最短的路径。相比于Dubins曲线只允许车辆向前运动，RS曲线同时允许车辆前向、后向运动，使得在某些情况下可以得出比 Dubins 曲线更优的解
• 约束性：曲线遵循机器人或车辆的运动学约束，例如最大转角、最大速度等。
• 多样性：存在不同类型的Reeds-Shepp曲线，例如直线-圆弧-直线（L-S-L）、直线-圆弧-反向圆弧-直线（L-S-R-S）等，以适应不同场景下的路径规划需求。

通过计算和生成Reeds-Shepp曲线，可以帮助机器人或车辆高效地规划路径并完成复杂的运动任务。

2 Reeds-Shepp曲线的运动模式

经过证明，RS曲线从起点到终点的最短路径一定是下面的组合之一

$$\left\{\begin{array}{c}C|C|C,CC|C,C|CC,CSC,C{C}_{\beta }|C_{\beta }C,C|C_{\beta }{C}_{\beta }|C,\\ C|C_{\pi /2}SC,CS{C}_{\pi /2}|C,C|C_{\pi /2}S{C}_{\pi /2}|C\end{array}\right\}$$

其中$C$表示圆弧运动，$S$表示直线运动，|表示车辆运动朝向发生改变。带$\pi /2$下标表示该段轨迹弧长对应的角度为$\pi /2$，带$\beta$下标表示相邻两段轨迹弧长对应的角度相等。将上述组合完整展开后对应如表所示的48种运动模式，其中+代表前行，-代表倒车。后续经过证明，$\left(L^{-}{R}^{+}{L}^{-}\right)$与$\left(R^{-}{L}^{+}{R}^{-}\right)$两种序列是多余的。

RS曲线在实现上的复杂度远远高于只有6种组合的Dubins曲线，考虑到序列间的对称关系，引入下面的变换简化曲线求解过程。

3 Reeds-Shepp曲线算法原理

3.1 坐标变换

类似Dubins曲线的思想进行坐标变换。在全局坐标系$xOy$中，设机器人起始位姿${\mathbf{p}}_s$、终止位姿${\mathbf{p}}_g$、最小转弯半径分别为$\left(x_s,y_s,\alpha \right)$、$\left(x_g,y_g,\beta \right)$与$R$。以${\mathbf{p}}_s$为新坐标系原点，位姿角$\alpha$方向为$x^{\prime }$轴，垂直方向为$y^{\prime }$轴建立新坐标系 ，同样考虑归一化最小转弯半径

p s ′ = [ 0 0 0 ] , p g ′ = [ ( x g cos ⁡ β + y g sin ⁡ β ) R ( − x g sin ⁡ β + y g cos ⁡ β ) R β − α ] \boldsymbol{p}_{s}^{'}=\left[ \begin{array}{c} 0\\ 0\\ 0\\\end{array} \right] , \boldsymbol{p}_{g}^{'}=\left[ \begin{array}{c} \left( x_g\cos \beta +y_g\sin \beta \right) R\\ \left( -x_g\sin \beta +y_g\cos \beta \right) R\\ \beta -\alpha\\\end{array} \right] ps′​= ​000​ ​,pg′​= ​(xg​cosβ+yg​sinβ)R(−xg​sinβ+yg​cosβ)Rβ−α​ ​

3.2 时间翻转(time-flip)

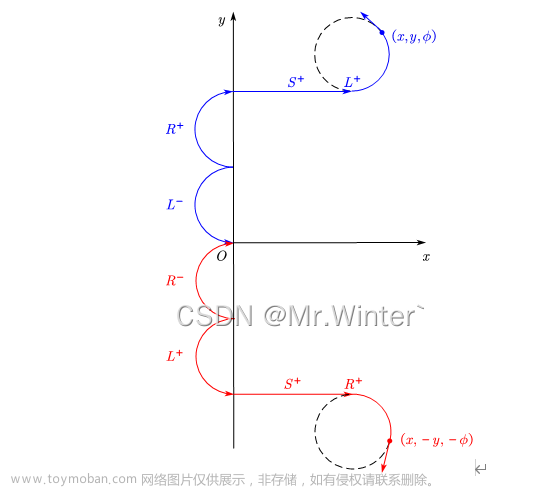
将计算曲线的运动方向全部取反，得到的新曲线与原曲线具有时间翻转关系。如图所示，以$L^{-}{R}^{+}{S}^{+}{L}^{+}\leftrightarrow L^{+}{R}^{-}{S}^{-}{L}^{-}$为例解释时间翻转：设实现了对$L^{-}{R}^{+}{S}^{+}{L}^{+}$的计算$f\left(x,y,\varphi \right)$，若用同样的函数计算$f\left(-x,y,-\varphi \right)$，并将各段路径取反，则等价于以轨迹$L^{+}{R}^{-}{S}^{-}{L}^{-}$到达$\left(x,y,\varphi \right)$。

3.3 反射变换(reflect)

将计算曲线的圆周运动类型全部取反，得到的新曲线与原曲线具有反射变换关系。如图所示，以$L^{-}{R}^{+}{S}^{+}{L}^{+}\leftrightarrow R^{-}{L}^{+}{S}^{+}{R}^{+}$为例解释仿射变换：设实现了对$L^{-}{R}^{+}{S}^{+}{L}^{+}$的计算$f\left(x,y,\varphi \right)$，若用同样的函数计算$f\left(x,-y,-\varphi \right)$，并将圆弧段类型取反，则等价于以轨迹$R^{-}{L}^{+}{S}^{+}{R}^{+}$到达$\left(x,y,\varphi \right)$。

3.4 后向变换(backwards)

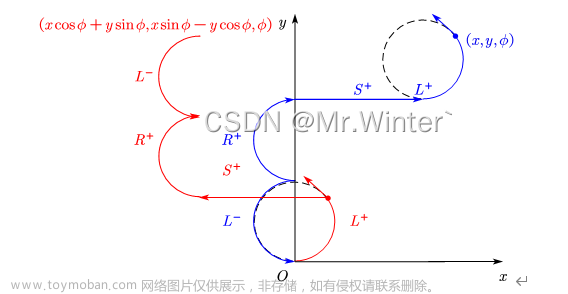
将计算曲线的轨迹段逆序，得到的新曲线与原曲线具有后向变换关系。如图所示，以$L^{-}{R}^{+}{S}^{+}{L}^{+}\leftrightarrow L^{+}{S}^{+}{R}^{+}{L}^{-}$为例解释后向变换：设实现了对$L^{-}{R}^{+}{S}^{+}{L}^{+}$的计算$f\left(x,y,\varphi \right)$，若用同样的函数计算$f\left(x\cos \varphi +y\sin \varphi ,x\sin \varphi -y\cos \varphi ,\varphi \right)$，并将计算曲线逆序，则等价于以轨迹$L^{+}{S}^{+}{R}^{+}{L}^{-}$到达$\left(x,y,\varphi \right)$。

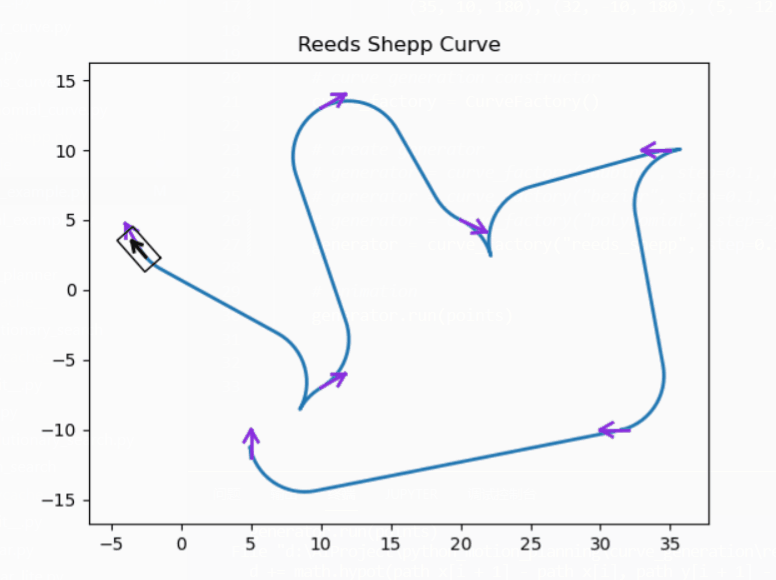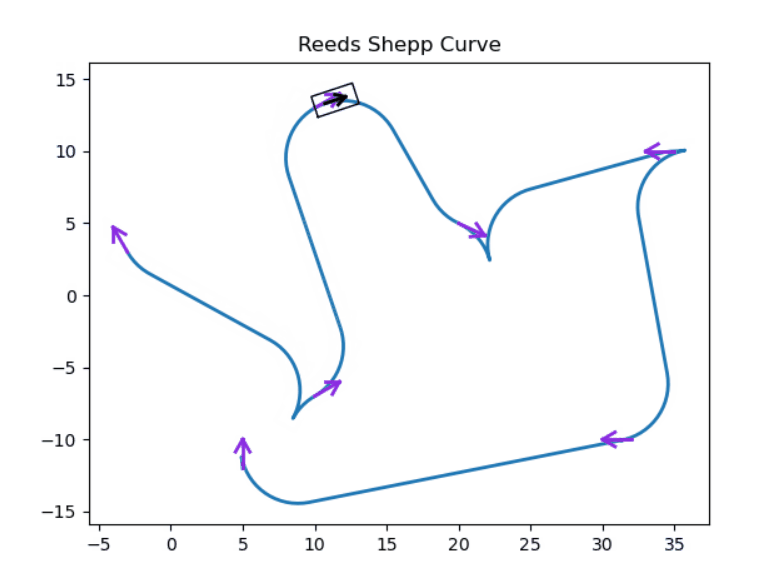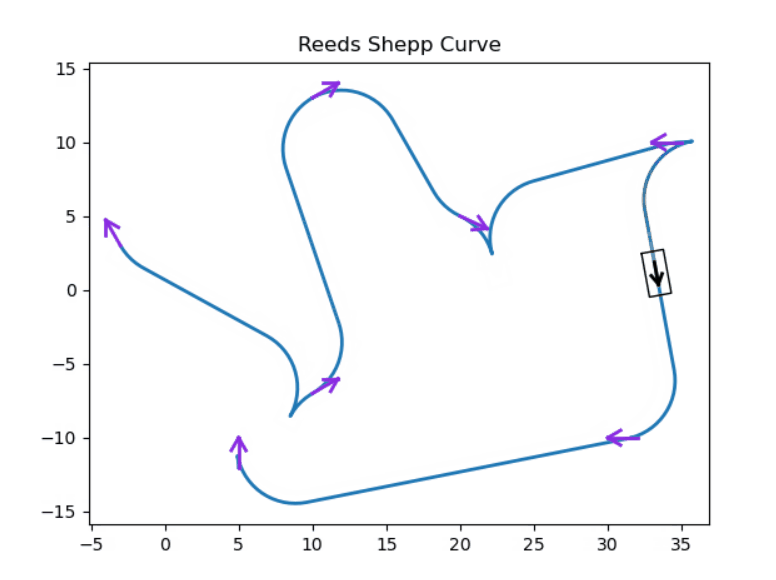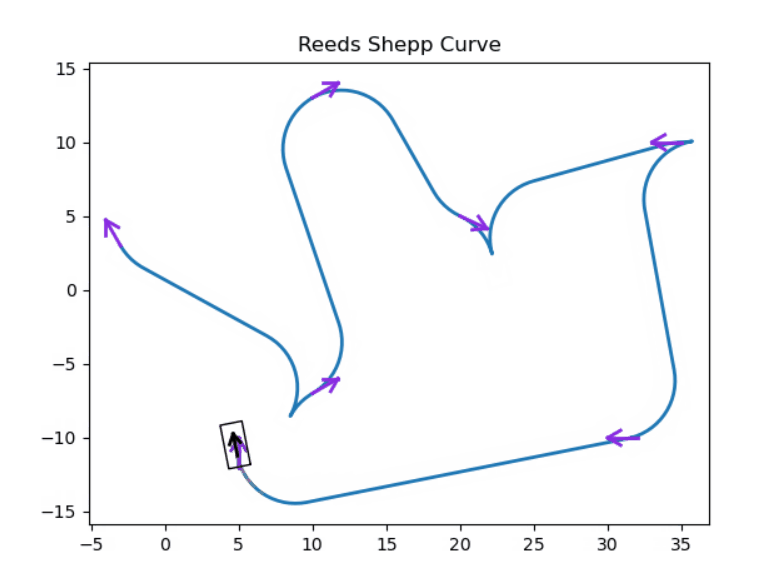
4 仿真实现

4.1 ROS C++实现

核心代码如下所示

Points2d ReedsShepp::generation(Pose2d start, Pose2d goal)
{
  ...

  // coordinate transformation
  ...

  // select the best motion
  RSPath best_path({ REEDS_SHEPP_MAX }, { REEDS_SHEPP_NONE });

  _update(SCS(x, y, dyaw), best_path);
  _update(CCC(x, y, dyaw), best_path);
  _update(CSC(x, y, dyaw), best_path);
  _update(CCCC(x, y, dyaw), best_path);
  _update(CCSC(x, y, dyaw), best_path);
  _update(CCSCC(x, y, dyaw), best_path);

  if (best_path.len() == REEDS_SHEPP_MAX)
    return path;

  // interpolation
  int points_num = int(best_path.len() / step_) + 6;

  int i = 0;
  for (size_t j = 0; j < best_path.size(); j++)
  {
    int m;
    double seg_length;
    best_path.get(j, seg_length, m);

    // path increment
    double d_l = seg_length > 0.0 ? step_ : -step_;
    double x = path_x[i];
    double y = path_y[i];
    double yaw = path_yaw[i];

    // current path length
    double l = d_l;
    while (fabs(l) <= fabs(seg_length))
    {
      i += 1;
      std::tie(path_x[i], path_y[i], path_yaw[i]) = interpolate(m, l, { x, y, yaw });
      l += d_l;
    }
    i += 1;
    std::tie(path_x[i], path_y[i], path_yaw[i]) = interpolate(m, seg_length, { x, y, yaw });
  }

  // remove unused data
  ...

  // coordinate transformation
  ...

  return path;
}

4.2 Python实现

核心代码如下所示

def generation(self, start_pose: tuple, goal_pose: tuple):
	sx, sy, syaw = start_pose
	gx, gy, gyaw = goal_pose

	# coordinate transformation
	...

	# select the best motion
	planners = [self.SCS, self.CCC, self.CSC, self.CCCC, self.CCSC, self.CCSCC]
	best_path, best_cost = None, float("inf")

	for planner in planners:
		paths = planner(x, y, dyaw)
		for path in paths:
			if path.path_length < best_cost:
				best_path, best_cost = path, path.path_length

	# interpolation
	points_num = int(best_cost / self.step) + len(best_path.lengths) + 3
	x_list = [0.0 for _ in range(points_num)]
	y_list = [0.0 for _ in range(points_num)]
	yaw_list = [0.0 for _ in range(points_num)]

	i = 0
	for mode_, seg_length in zip(best_path.ctypes, best_path.lengths):
		# path increment
		d_length = self.step if seg_length > 0.0 else -self.step
		x, y, yaw = x_list[i], y_list[i], yaw_list[i]
		# current path length
		length = d_length
		while abs(length) <= abs(seg_length):
			i += 1
			x_list[i], y_list[i], yaw_list[i] = self.interpolate(mode_, length, (x, y, yaw))
			length += d_length
		i += 1
		x_list[i], y_list[i], yaw_list[i] = self.interpolate(mode_, seg_length, (x, y, yaw))
	
	# failed
	...

	# remove unused data
	...

	# coordinate transformation
	...

	return best_cost / self.max_curv, best_path.ctypes, x_list_, y_list_, yaw_list_

4.3 Matlab实现

核心代码如下所示

function [x_list, y_list, yaw_list] = generation(start_pose, goal_pose, param)  
    % coordinate transformation
    ...

    % select the best motion
    planners = ["SCS", "CCC", "CSC", "CCCC", "CCSC", "CCSCC"];
    best_cost = inf;
    best_path = [];

    for i=1:length(planners)
        planner = str2func(planners(i));
        paths = planner(x, y, dyaw);
        for j=1:length(paths)
            if paths(j).len < best_cost
                best_path = paths(j);
                best_cost = paths(j).len;
            end
        end
    end
    
    % interpolation
    points_num = floor(best_cost / param.step) + length(best_path.segs) + 3;
    x_list_ = zeros(points_num);
    y_list_ = zeros(points_num);
    yaw_list_ = zeros(points_num);

    i = 1;
    for j = 1:length(best_path.segs)
        m = best_path.ctypes(j);
        seg_length = best_path.segs(j);
        
        % path increment
         if seg_length > 0.0
            d_length = param.step;
         else
            d_length = -param.step;
         end
        x = x_list_(i); y = y_list_(i); yaw = yaw_list_(i);
        
        % current path length
        l = d_length;
        while abs(l) <= abs(seg_length)
            i = i + 1;
            new_pt = interpolate(m, l, [x, y, yaw], param);
            x_list_(i) = new_pt(1); y_list_(i) = new_pt(2); yaw_list_(i) = new_pt(3);
            l = l + d_length;
        end
        i = i + 1;
        new_pt = interpolate(m, seg_length, [x, y, yaw], param);
        x_list_(i) = new_pt(1); y_list_(i) = new_pt(2); yaw_list_(i) = new_pt(3);
    end
    
    % remove unused data
    ...
    
    % coordinate transformation
    ...
end

完整工程代码请联系下方博主名片获取

🔥 更多精彩专栏：文章来源地址https://www.toymoban.com/news/detail-843401.html

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

到了这里，关于曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！