目录
前言
A.建议
B.简介
一 代码实现
二 时空复杂度
A.循环实现
a.时间复杂度(Time Complexity):
b.空间复杂度(Space Complexity):
B.递归实现
a.时间复杂度(Time Complexity):
b.空间复杂度(Space Complexity):
三 优缺点
A.循环实现
a.优点:
b.缺点:
c.总结:
B.递归实现
a.优点:
b.缺点:
c.总结:
四 现实中的应用
前言
A.建议
1.学习算法最重要的是理解算法的每一步,而不是记住算法。
2.建议读者学习算法的时候,自己手动一步一步地运行算法。
B.简介
在C语言中,使用欧几里得算法(Euclidean Algorithm)求两个正整数的最大公约数(Greatest Common Divisor, GCD)可以通过连续做除法和取余操作实现。
一 代码实现
下面是一个使用循环实现的简单示例:
#include <stdio.h>
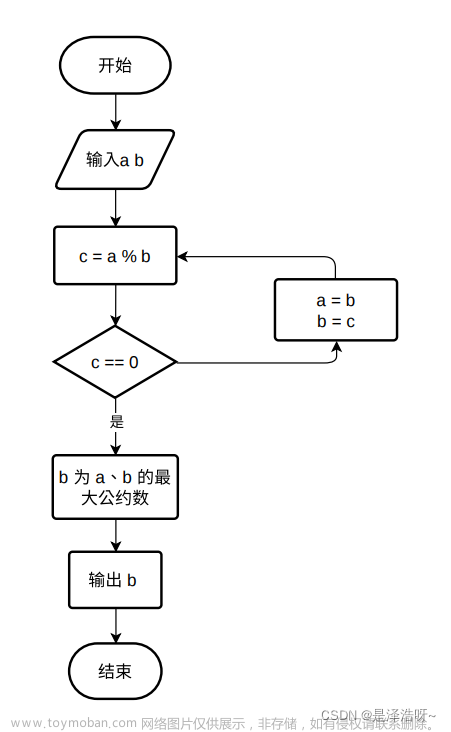
int gcd(int a, int b) {
// 辗转相除法(欧几里得算法)
while (b != 0) {
int temp = a % b;
a = b;
b = temp;
}
return a; // 当b为0时,a即为最大公约数
}
int main() {
int num1, num2;
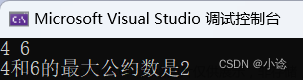
printf("请输入两个整数:");
scanf("%d %d", &num1, &num2);
// 求最大公约数
int result = gcd(num1, num2);
printf("这两个数的最大公约数是:%d\n", result);
return 0;
}在这个gcd函数中,我们首先检查b是否为0。如果不是0,我们就更新a为a % b的值,同时更新b为原来的a的值。这样,每一次循环都在逐步缩小问题规模,直到找到最大公约数。当b变为0时,我们知道a已经是所求的最大公约数。
如果你想要一个递归版本的欧几里得算法,那么它可以这样实现:
int gcd_recursive(int a, int b) {
if (b == 0) {
return a;
} else {
return gcd_recursive(b, a % b);
}
}
// 在main函数中调用gcd_recursive函数替代gcd函数即可在这个递归版本中,函数gcd_recursive会一直调用自身,每次都将较大的数作为被除数,较小的数及其余数作为下次调用的除数和被除数,直到余数为0时返回除数。
二 时空复杂度
A.循环实现
a.时间复杂度(Time Complexity):
在欧几里得算法中,每次循环我们都用较小的数去除较大的数,并更新余数。可以观察到,每次循环后,至少有一个数(这里是b)变小了。当b变为0时,循环结束。由于每次循环都能使得b至少减半(并非严格意义上的每次一半,但总体趋势如此),因此,循环次数大致等于log以2为底的b(初始时的较小数)。但是在最坏情况下,例如当a和b互质时,循环次数最多等于min(a, b)。因此,算法的时间复杂度是 O(min(a, b))。
b.空间复杂度(Space Complexity):
在这段代码中,我们只使用了固定数量的额外空间:除了输入的两个整数num1和num2之外,还使用了一个临时变量temp来存储余数。无论输入的整数有多大,temp占用的空间始终保持不变。因此,算法的空间复杂度是 O(1),即常数空间复杂度。这意味着空间需求不随输入规模的增大而增加。
B.递归实现
a.时间复杂度(Time Complexity):
递归版欧几里得算法同样遵循每次循环(递归调用)都将较小数替换为较大数与较小数的余数这一规则。与循环版本一样,递归版本的时间复杂度也是 O(log min(a, b)) 或者在最坏情况下为 O(min(a, b)),因为每次递归调用后,至少有一个参数的大小在减小。
b.空间复杂度(Space Complexity):
在递归版本中,每次函数调用都会在内存栈中保留当前调用的信息,包括局部变量和返回地址等。对于每一次递归调用,算法都会增加一层递归深度,直至基本情况(b == 0)发生并开始回溯。因此,递归深度在最坏情况下也是 min(a, b)。所以,递归版欧几里得算法的空间复杂度为 O(min(a, b)),这是因为递归栈的深度与输入的大小成正比。不过要注意的是,在实际编程环境中,由于栈空间有限,过于大的输入可能导致栈溢出错误。
三 优缺点
A.循环实现
a.优点:
-
简洁性:循环实现的欧几里得算法代码简洁明了,易于理解和实现,不需要额外的递归栈空间。
-
效率:循环版本的算法在实践中通常比递归版本更快,因为它避免了递归调用带来的函数调用开销,尤其是在支持尾递归优化的语言中优势更为明显。
-
空间效率:该算法的空间复杂度仅为O(1),只需要固定的几个变量就可以完成计算,特别适合处理大型数据时对内存要求较低的场景。
-
无栈溢出风险:相比递归版本,循环版本不存在因递归深度过深导致的栈溢出问题,这对于输入较大的数特别有利。
b.缺点:
-
递归思维弱化:相比于递归版本,循环实现不利于直观展示算法的递归性质,对于教学和理论分析可能不如递归版本清晰。
-
可读性:虽然简洁,但对于初次接触的人来说,可能需要更多时间去理解循环内部是如何不断更新a和b以逼近最大公约数的过程。
-
灵活性:递归版本更容易进行泛化,例如扩展到扩展欧几里得算法(不仅求最大公约数,还能求模逆元等),循环实现时需要手动添加更多的控制逻辑。
c.总结:
总的来说,这个循环实现的欧几里得算法在实际编程中是非常实用且高效的,适用于大部分应用场景,并且由于其优良的时间和空间复杂度,成为了求解最大公约数问题的标准算法之一。然而,在强调递归思想的教学或易于模块化的编程环境中,递归版本可能更具吸引力。
B.递归实现
a.优点:
-
递归思维清晰:递归实现的欧几里得算法直观展示了算法本身的递归性质,便于理解算法的逻辑结构,特别是在教学和理论分析中。
-
易于扩展:递归版本更适合进一步扩展到类似扩展欧几里得算法等更复杂的场景,只需稍作修改,无需重新设计循环逻辑。
-
模块化:递归函数具有较好的模块化特性,每一个递归调用都独立处理一部分问题,有利于代码重用和维护。
b.缺点:
-
性能开销:递归版本相较于循环版本可能存在更多的函数调用开销,尤其是在不支持尾递归优化的编译器环境下,可能导致运行速度较慢。
-
空间复杂度较高:递归实现的欧几里得算法的空间复杂度为O(min(a, b)),因为在递归过程中,每次函数调用都会占用一定的栈空间。对于较大的输入值,可能造成栈溢出的风险。
-
理解难度:对于不熟悉递归原理的程序员而言,递归版本的代码可能相对较难理解,特别是对于如何通过不断调用自身解决问题的过程。
-
调试困难:递归调用链较长时,出现错误时的调试难度可能增大,需要理解递归调用栈的状态才能定位问题所在。
c.总结:
综合来看,虽然递归实现的欧几里得算法在表达力和扩展性上有一定优势,但在实际应用中,尤其是在对时间和空间效率有较高要求的情况下,循环实现通常更为适用。而在教学和理论研究等场景下,递归版本因其直观性和递归性质的展现,具有独特的价值。
四 现实中的应用
欧几里得算法(Euclidean Algorithm)求最大公约数在现实生活中有着广泛的应用,以下是几种常见场景:
-
密码学:
- 在RSA公钥密码体系中,计算两个大整数的最大公约数是至关重要的步骤,用于验证公钥的有效性和安全性。通过欧几里得算法找到两个大素数的乘积的因数,可以确保加密的安全强度。
-
数字信号处理:
- 在数字音乐、视频压缩编码等领域,需要对采样频率、帧率等进行转换时,通常涉及到了两个整数之间的同步关系,通过求最大公约数来确定两个周期信号的最小公倍数,有助于进行精准的同步和采样率转换。
-
计算机图形学:
- 在渲染引擎中,为了使纹理贴合几何体表面平滑无缝,需要对纹理坐标进行调整,欧几里得算法可以帮助找到纹理坐标的重复周期,从而实现纹理的完美拼接。
-
网格划分与计算几何:
- 在计算机辅助设计(CAD)和科学计算中,欧几里得算法可用于网格划分,确保不同尺寸的对象能够均匀分布或者按比例缩放,同时保持整数边界的完整性。
-
计算机网络:
- 在网络通信协议中,有时需要找到数据包传输的最佳间隔时间,此时就需要计算发送端和接收端各自时间片的最小公倍数,而这需要先知道它们的最大公约数。
-
软件开发与编程实践:
- 编程中处理日期、时间、循环等问题时,经常遇到周期性计算,通过求最大公约数可以简化循环次数或找出循环规律。
-
数论问题:
- 在纯数学研究及数论相关的算法设计中,欧几里得算法是最基础的工具之一,许多复杂问题的求解都要先经过求最大公约数这一步骤。
-
金融与经济领域:文章来源:https://www.toymoban.com/news/detail-843513.html
- 在股票交易、贷款利率计算等方面,有时候需要找到多个时间周期的最小公倍数,这就需要先计算最大公约数。
总之,欧几里得算法在众多需要处理整数关系、周期性问题、加密安全、数据同步等多个方面都有实际应用,可以说是计算机科学和工程领域不可或缺的基础工具之一。文章来源地址https://www.toymoban.com/news/detail-843513.html
到了这里,关于C语言经典算法之Euclidean算法求最大公约数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!