二维矩阵的前缀和,我们可以通过求前缀和来把求二维矩阵的求某一块的和,从时间复杂度O(n^2)变成O(1)常数级,大大降低了时间复杂度
文章目录
前言
一、二维矩阵的前缀和应该怎么做?
1.引入一个二维数组
2.二维前缀和矩阵数组
3.推出二维矩阵前缀和的公式计算
3.1 代码如下
二.求子矩阵的和
1.算法思路
编辑
2 子矩阵和公式推导
三、测试数据
1.代码如下(示例):
2.测试数据
2.1 测试数据如下
2.2运行结果如下
2.3样例结果解释
总结
前言
二维矩阵的前缀和,我们可以通过求前缀和来把求二维矩阵的求某一块的和,从时间复杂度O(n^2)变成O(1)常数级,大大降低了时间复杂度
提示:以下是本篇文章正文内容,下面案例可供参考
一、二维矩阵的前缀和应该怎么做?
1.引入一个二维数组
int[][] arr = {
0 0 0 0 0
0 1 7 2 4
0 3 6 2 8
0 2 1 2 3
}2.二维前缀和矩阵数组
二维矩阵前缀和和一维矩阵大同小异,我们可以定义矩阵前缀,是以右下角元素为主的矩阵的元素和。
我们可以一步一步的推出二维前缀矩阵里面各个位置的值。设置前缀和矩阵为s例如:我们求s[1][1]的值。
注:我们在初始位置多添加了一行、一列,因为原arr数组这些地方是没有值的
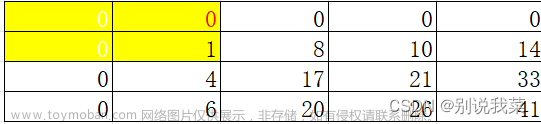
图2.1
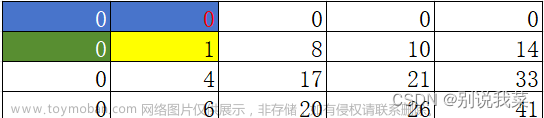
图2.2

图2.3
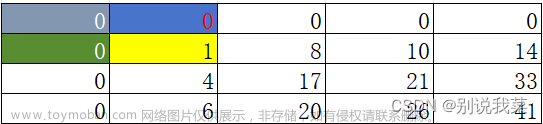
图2.4
即求图2.1黄色区域的面积=图2.2蓝色区域的面积+图2.3绿色区域的面积-图2.4紫色区域的面积(注因s[0][0]即图2.4紫色区域的面积被重复计算了)+arr[1][1]。
s[1][1] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + arr[1][1](注:里面的i=1,j=1)
3.推出二维矩阵前缀和的公式计算
由上述式子推出的s[1][1]的值我们可以推广到公式s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + arr[i][j]
3.1 代码如下
int[][] s = new int[n+1][m+1];
for(int i = 1;i <= n;i++ ){
for(int j = 1;j <= m;j++){
s[i][j] = s[i-1][j] + s[i][j-1]-s[i-1][j-1] + arr[i][j];
}
}二.求子矩阵的和
1.算法思路
我们给定4个参数x1 y1 x2 y2,即求二维数组从arr[x1][y1]到arr[x2][y2]的区间和(图1.1蓝色区域的面积)
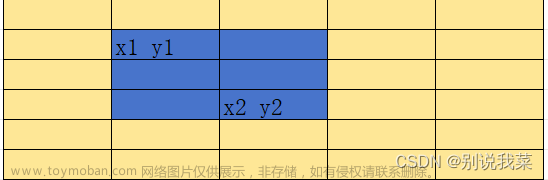
图 1.1
图1.2
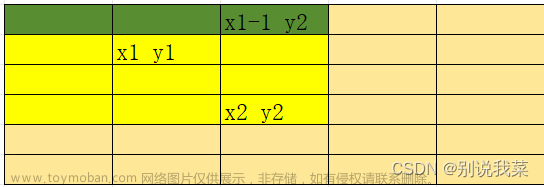
图 1.3

图1.4

图1.5
我们可以用图1.2黄色区域的面积即s[x2][y2]-图1.3绿色区域的面积即s[x1-1][y2]-图1.4白色区域的面积s[x2][y1-1]+图1.5红色区域的面积s[x1-1][y1-1],就可以求出子矩阵的和。(注:跟我们推导二维前缀和数组的过程基本一样,同样是要加上被重复减去的部分即图1.5中的红色区域的面积)
2 子矩阵和公式推导
公式为 result = s[x2][y2]-s[x1-1][y2]-s[x2][y1-1] + s[x1-1][y1-1]
代码如下:
int x1 = nextInt();
int y1 = nextInt();
int x2 = nextInt();
int y2 = nextInt();
pw.println(s[x2][y2]-s[x1-1][y2] - s[x2][y1-1]+s[x1-1][y1-1]);三、测试数据
1.代码如下(示例):
import java.io.*;
public class 子矩阵的和 {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static void main(String[] args) throws Exception{
int n = nextInt();
int m = nextInt();
int q = nextInt();
int[][] arr = new int[n+1][m+1];
for (int i = 1; i <= n; i++) {
for(int j = 1;j <= m;j++){
arr[i][j] = nextInt();
}
}
int[][] s = new int[n+1][m+1];
//构建前缀和矩阵
for(int i = 1;i <= n;i++ ){
for(int j = 1;j <= m;j++){
s[i][j] = s[i-1][j] + s[i][j-1]-s[i-1][j-1] + arr[i][j];
}
}
pw.println("------------------------");
pw.println("前缀和矩阵如下:");
for(int i = 1;i <= n;i++ ){
for(int j = 1;j <= m;j++){
pw.print(s[i][j]+" ");
}
pw.println();
}
pw.println("------------------------");
//测试样例
while(q-- > 0){
int x1 = nextInt();
int y1 = nextInt();
int x2 = nextInt();
int y2 = nextInt();
pw.println(s[x2][y2]-s[x1-1][y2] - s[x2][y1-1]+s[x1-1][y1-1]);
}
pw.flush();
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
}
2.测试数据
2.1 测试数据如下
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 42.2运行结果如下
------------------------
前缀和矩阵如下:
1 8 10 14
4 17 21 33
6 20 26 41
------------------------
17
27
212.3样例结果解释
17 = 1 + 7 + 3 + 6
27 = 3 + 6 + 2 + 8 +2 + 1 + 2 + 3
21 = 2 + 4 + 2 + 8 + 2 + 3 文章来源:https://www.toymoban.com/news/detail-843748.html
总结
上述的重点还是在如何推导二维矩阵的前缀和矩阵,知道这个推导过程,对于后面的求子矩阵的和思路其实一样。文章来源地址https://www.toymoban.com/news/detail-843748.html
到了这里,关于二维矩阵的前缀和+子矩阵的和-java的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!










