动态规划dp详解（破解之道，就在其中）-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划dp详解（破解之道，就在其中）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.什么是动态规划

定义：动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

简单来说，动态规划其实就是，给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后呢，把子问题答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。

例子：比如我给这样的一个数列，-10, 10, 20, 30，-20，这时题目让我们求出最大连续字段和，我们一眼就可以看出来10，20,30这个连续的字段和一定是最大的，但要是字段有几百个，几千个呢。有人会用很多个for循环，比如从-10开始，我再用一个for循环计算从-10开始的最大连续字段和，结束后再从10开始，最后比较一下，但这样用for循环嵌套的方式往往会使得我们时间超限。因此这时候采用动态规划就显得很明智了。

二.解释例题上代码

我们回到上述例题来看，如果要我们求连续条件下的最大字段和，又不采用for循环嵌套的条件下，我们最好的方法实际上就是用一次for循环解决战斗。

for(int i=1;i<=n;i++){
        dp[i]=max(a[i],dp[i-1]+a[i]);
    }

这里的a[i]表示的就是题目给出的序列，dp[i]我们这里表示为从1到i的序列下最大的连续子段和。我们还是以-10,10,20,30，-20举例。

我们从i=1开始，当i=1时，我们现在只能选取a[i]也就是a[1]为1到i的最大值，当i=2时，我们可以发现从1到2中，连续最大字段和为10，而不是-10+10，因此，我们选择dp[i]=max(a[i],dp[i-1]+a[i])作为状态转移方程（关键语句），每次我们比较a[i]和dp[i-1]+a[i]的大小，通过这种方式，我们将从1到n的最大字段和分解为从1到1，从1到2...这种小问题进行处理，时间复杂度为n,这样就不会出现时间超限的情况了。

一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等，都是动态规划的经典应用场景。

三.动态规划思路分析

动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。 并且动态规划一般都是自底向上的。

动态规划思路分析：

穷举分析
确定边界
找出规律，确定最优子结构
写出状态转移方程

我们就根据上面例题来讲解一下：

1. 穷举分析：一般情况下，由于每道题题目不同往往需要我们去分析题目要求我们干什么，因此这时候我们往往会穷举几个例子进行分析。

在上面的题中，我们发现，当i=1时，我们现在只能选取a[i]也就是a[1]为1到i的最大值，当i=2时，我们可以发现从1到2中，连续最大字段和为10，而不是-10+10，这样我们就会发现，每一次取值是，我们由于要选择连续的子段，一次我们就会选择要么是a[i]要么是紧跟上上一次的字段和加上这次的a[i]，我们需要判断一下谁大一点即可。

2.确定边界：有的时候往往在i=1或i=n等边界值是要确实dp[i]的值，这里需要注意一下。

3.找出规律，确定最优子结构：我们穷举时可以发现，因为让我们找最优连续子序列，那么从1到i中我们找到从1到i-1中的最短连续子序列之后，是不是就应该比较下一步到底是加不加a[i]这个值，还是说最大的就是a[i]。

4.写出状态转移方程：当我们在第一步时我们知道题目大概思路后，我们要列出代码中最需要的部分，也就是状态转移方程，顾名思义，就是从i=1注意到i=2等其他状态的方程。我们首先要确定dp[i]表示什么，到底是从1到i中连续子段和最大值还是其他很玄幻的东西。我们这里认为dp[i]表示的就是从1到i中连续子段和最大值。那么根据3中找出的规律就可以列出状态转移方程了，也就是dp[i]=max(a[i],dp[i-1]+a[i]);

但是，这道题还有最后一个关键的地方，就是我们每次求的是从1到i的最大连续字段和，那么实际上最终结果应当为你从1到i中最大连续字段和的最大值，因为在我们的状态转移方程里，我们每次都不可避免的取到a[i]这个值，就比如你运行下面的这段代码，你运行-10,10,20,30，-20，这个数列，你会发现最终结果为40而不是60，只就是因为到最后我们总不可避免的加上a[i],

for(int i=1;i<=n;i++){
        dp[i]=max(a[i],dp[i-1]+a[i]);
    }

那怎么解决呢，我们发现在这个数列里从1到4的连续最大子序列为60，也就是说我们只要最后再遍历一遍dp数组，找出其中最大值即可。

int ma=-0x3f3f3f;
for(int i=1;i<=n;i++){
    if(ma<=dp[i]){
      ma=dp[i];
    }
}

至此，dp的思想我想应该就讲的差不多了，至于dp各种类型问题，虽然有的是板子（放在我下一篇博客里吧就），但都需要我们依靠上面的思路来解决dp这种问题，因此有板子但大部分没什么用，重要的是你真正能写出状态转移方程。

四.例题（饭后小甜点）

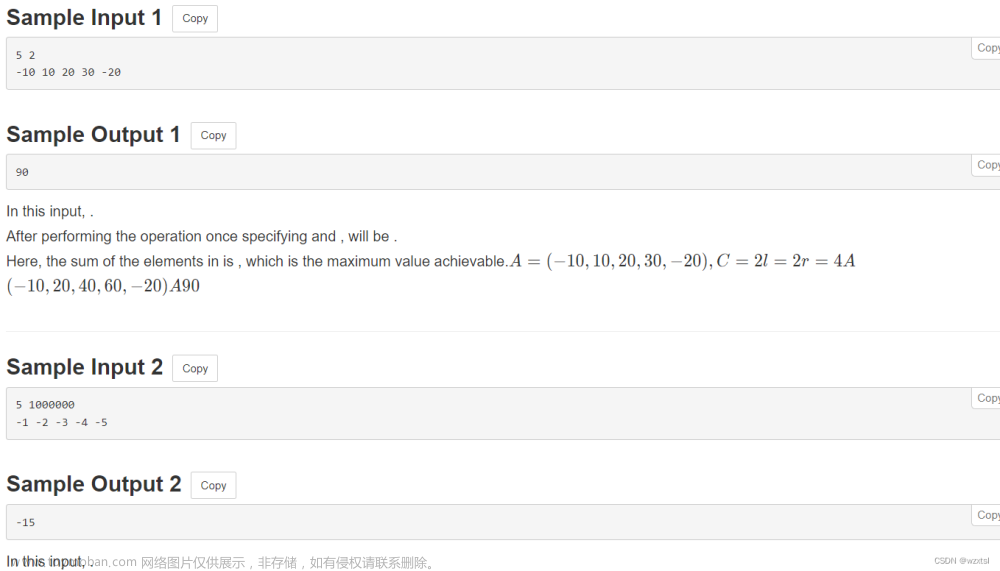
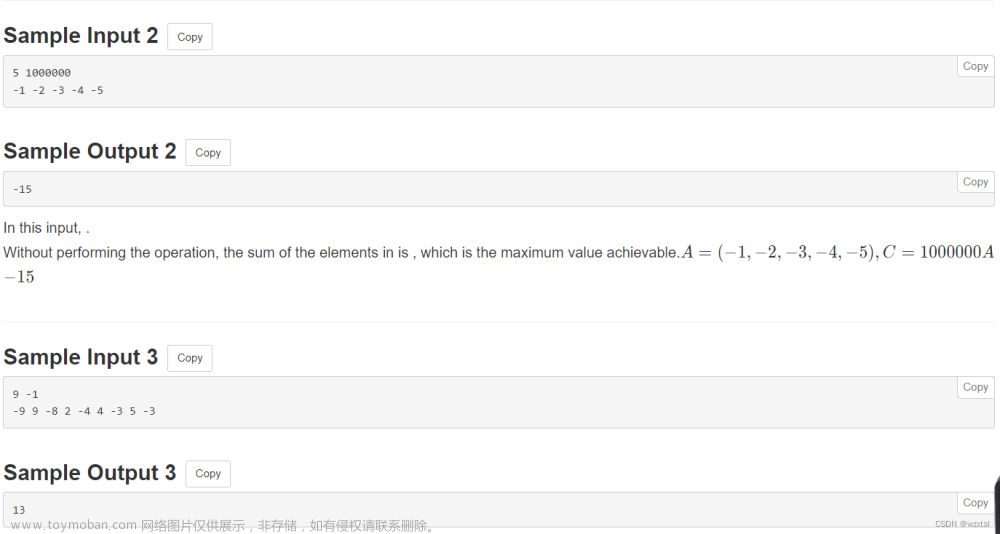动态规划dp详解（破解之道，就在其中）,动态规划,算法

动态规划dp详解（破解之道，就在其中）,动态规划,算法代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+7;
long long a[N];
long long b[N];
long long s[N];
long long dp[N];
int main(){
    long long n,c;
    cin>>n>>c;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=a[i]*(-1);//b[i]用-a[i]表示是为了后面方便求a[i]的最小连续子段和
        s[i]=s[i-1]+a[i];
    }
    long long ans=0;
    dp[0]=0;
    if(c>0){
        //求最大连续子段和
        for(int i=1;i<=n;i++){
        dp[i]=max(a[i],dp[i-1]+a[i]);//状态转移方程
        }
        long long ma=-0x3f3f3f;
        for(int i=1;i<=n;i++){
            if(ma<=dp[i]){
                ma=dp[i];
            }
        }
        if(ma>=0){
            ans=s[n]+ma*(c-1);
            cout<<ans<<endl;
        }else{
            cout<<s[n]<<endl;
        }
    }else if(c<=0){
        //求最小连续子段和
        //这里我们求b[i]的最大子段和，也就是-a[i]的最大子段和，最后取负数便可求出最小连续子段和
        for(int j=1;j<=n;j++){
        dp[j]=max(b[j],dp[j-1]+b[j]);//状态转移方程
        }
        long long ma=-0x3f3f3f;
        for(int i=1;i<=n;i++){
            ma=max(ma,dp[i]);
        }
        ma=ma*(-1);
        if(ma>=0){
            cout<<s[n]<<endl;
        }else{
            ans=s[n]+ma*(c-1);
            cout<<ans<<endl;
        }
    }
    system("pause");
    return 0;
}

至此，完结撒花！！！

请点关注，入坑不易，下次待我持续发力！文章来源地址https://www.toymoban.com/news/detail-843764.html

到了这里，关于动态规划dp详解（破解之道，就在其中）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！