👂 如果当时2020(不曾遗忘的符号) - 许嵩/朱婷婷 - 单曲 - 网易云音乐
👂 一个深爱的女孩 - 本兮 - 单曲 - 网易云音乐
半年前写了一半的博客.......(2023/7/14),今天花6小时给它补充完毕......
目录
🌼补充知识
🌳分类
🌼一, 1158: 八皇后
🌼二, 3472. 八皇后
🌼三,P1605 迷宫
🌼四,P1434 [SHOI2002] 滑雪
🌳AC 记忆化dfs
🌼五,指数型枚举
🌼六,排列型枚举
🌼七,组合型枚举
🌼八,油田 Oil Deposits
🌼九,P1019 [NOIP2000 提高组] 单词接龙
🍔总结
🌼补充知识
精益求精
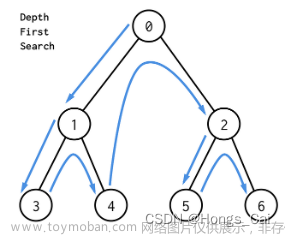
在开始之前,我想先对BFS和DFS作个简单的区分
dfs可以用递归来写,也可以用栈来写;bfs可以用数组模拟队列,也可以直接stl的队列
dfs很难找到最优解,只用来找到某个解,内存消耗较小;bfs则适用于找最优解,但不适用于深层次的搜索
dfs如果需要回溯,就需要取消标记;而bfs不需要取消标记
接下来谈谈最近dfs刷题的思考:
关于,为什么有些dfs需要在标记,递归后进行取消标记,而另一些题目则不需要取消标记呢?
eg1: 给定起点,走5步,求所有可能到达的点
eg2: 给定起点,不限制步数,求能否到达终点
问题1限制了步数,所以经过某点的路径会影响结果,那么就需要多次经过同一个点(意味着需要回溯),所以需要取消标记
而问题2经过某点的路径不影响结果(不限制步数),所以不需要多次经过同一个点(不需要回溯),所以不需要取消标记
一次能把所有点走完,不需要取消标记(不需要回溯),走过的点就不会再走了
而如果部分路径需要多次访问,这时就需要回溯取消标记了,不然就没法访问了
-- -- End~
知识点
下面,先结合百度,CSDN,博客园,知乎,《啊哈算法》,oi-wiki,增加对dfs的了解
(1条消息) 《啊哈算法》第四章之深度优先搜索_码龄?天的博客-CSDN博客
DFS(搜索) - OI Wiki (oi-wiki.org)
深度优先搜索 - AcWing
🌳分类
1,n皇后
基于国际象棋规则,皇后可以攻击(1)同一行(2)同一列,
(3)同一斜线(包括主对角线和副对角线的方向) 的其他单位
在n * n的棋盘中,放置n个皇后,使它们互相之间不攻击
2,迷宫
迷宫里有几个点:
1,递归是很多人难以理解的,比如return;
2,模板则是,遍历 + 判断目标,其中遍历里的回溯 = 标记 + 递归 + 取消标记
3,走迷宫需要建立一个二维数组保存地图,并且需要一个二维方向数组
《啊哈算法》第四章之深度优先搜索_码龄?天的博客-CSDN博客
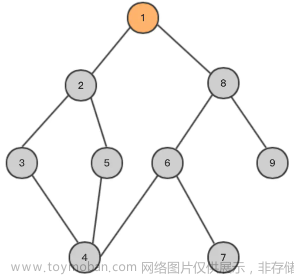
3,油田
有点类似记忆化dfs的过程,但是完全不一样。
记忆化dfs可以用一个数组保存过程,比如滑雪那题,找最长路程,后续遍历到以前走过的点,就不需要再遍历了,类似剪枝。
而油田,对每个点dfs后,将访问过的点在地图上直接操作(标记),省去了 vis[][] 标记数组,节省了空间。
4,单词接龙
5,记忆化dfs
6,dfs枚举
对dfs枚举做个总结,
1,都需要一个数组a[]来保存最后输出的答案
2,排列型枚举,就是全排列,dfs模板,可以画递归树辅助理解
3,组合型枚举,1~n中取m个数,由于是组合,打算顺序视作相同,如果处理呢?只需要保证后一个数 > 前一个数,加个 if 判断(还可以剪枝)
4,指数型枚举,和排列型稍作区别,排列型需要对每一个数进行选择,而指数型,只需要判断选 / 不选,不需要for(... i ~ n ...)
(1)指数型枚举
1~n中随机选择任意多个,输出所有方案的选择
int vis[N];
void dfs(int x)
{
//到达边界
if(x == n) {
...
return;
}
//只有选 / 不选两种可能
//选
vis[x] = 1; //标记选择
dfs(x + 1); //递归
vis[x] = 0; //取消标记
//不选
dfs(x + 1); //vis[x] = 0; 默认未选择
}(2)组合型枚举
(3)排列型枚举(全排列)
🌼一, 1158: 八皇后
P1158 - 八皇后 - New Online Judge (ecustacm.cn)
标签:基础题,USACO,深度优先搜索

下面展示两种做法
1,利用b, c, d三个数组,分别标记在某一列,某一右斜,某一左斜是否冲突
2,然后dfs(int row)的参数就是行数,避免了对第几行是否可行的讨论
3,在遍历的过程中递归
4,不是标准的dfs模板,但是做法值得学习,而且复杂度比直接套模板低
row就是行,j 就是列,row - j 就是主对角线,row + j 就是副对角线(row - j + 13防止负数)
主对角线,row - j 相等;副对角线,row + j 相等

AC 代码
#include<iostream>
int a[100], b[100], c[100], d[100];
int ans = 0, n;
using namespace std;
void dfs(int row)
{
for(int j = 1; j <= n; ++j)
if(b[j] == 0 && c[row - j + 13] == 0 && d[row + j] == 0) {
a[row] = j;
//标记
b[j] = 1; //列已放置
c[row - j + 13] = 1; //主对角线
d[row + j] = 1; //副对角线
if(row == n) { //得到一个答案
ans++;
if(ans <= 3) {
for(int k = 1; k <= n; ++k)
cout<<a[k]<<" ";
cout<<endl;
}
}
else dfs(row + 1); //递归
//取消标记
b[j] = 0;
c[row - j + 13] = 0;
d[row + j] = 0;
}
}
int main()
{
cin>>n;
dfs(1);
cout<<ans;
return 0;
}
/*
a[row] = j放在第row行第j列
b[j] = 1第j列已放置
c[row - j + 13]主对角线已放置, +13防止下标为负
d[row + j]副对角线已防放置
*/AC 代码2
标准的dfs模板
代码2耗时555ms,代码1耗时355ms
关于abs的解释
实际上还是对行,列,主,副对角线的判断,不过这次主副对角线一行搞定
dfs中for循环里,要放置的是第step + 1行, 第 j 列。前面遍历的是第 i 行第 a[i] 列
行差值(绝对值) == 列差值 表示主副对角线有重合,就break
坑
代码第 19 行
for(int i = 1; i <= step; ++i) //第 i 行1) 遍历到 step 是因为,后面的行还没放置到
2) i <= step 是因为,主函数中 step 从 0 开始,此时 1 ~ step 表示,遍历到当前行的
前一行,如果 step 从 1 开始,只能 i < step,否则就会 WA
#include<iostream>
using namespace std;
int a[100], vis[100], n, ans; //vis[j]统计第 j 列是否被放置
void dfs(int step) //已放置step个皇后, 第 step + 1行
{
if(step == n) {
ans++;
if(ans <= 3) {
for(int k = 1; k <= n; ++k)
cout<<a[k]<<" ";
cout<<endl;
}
return;
}
for(int j = 1; j <= n; ++j) { //第 j 列
if(!vis[j]) { //第 j 列未放置
int flag = 1;
for(int i = 1; i <= step; ++i) //第 i 行
if(abs(step + 1 - i) == abs(j - a[i])) {
flag = 0;
break;
}
if(flag) { //可以放置
a[step + 1] = j;
vis[j] = 1; //标记
dfs(step + 1); //递归
vis[j] = 0; //取消标记
}
}
}
}
int main()
{
cin>>n;
dfs(0); //第1行开始
cout<<ans;
return 0;
}🌼二, 3472. 八皇后
3472. 八皇后 - AcWing题库
标签:中等,DFS,北京大学考研机试题

在第一题的基础上,将结果存起来,不用排序!!!
主要目的是练手,再敲一遍,增加熟练度
卡点
1,在dfs函数中,就可以用 *= 10的方法操作
2,最好不要用string b[]这样保存,否则还得加数字转化为字符串再 +=
AC 代码
#include<iostream>
#include<cmath>
using namespace std;
// 第 i 行第 a[i] 列, b[]每一组答案, vis[] 某一列已放置
int a[10], b[100], vis[10], cnt = 1;
void dfs(int r)
{
if (r == 9) { // 放置完毕
for (int i = 1; i <= 8; ++i) {
b[cnt] *= 10;
b[cnt] += a[i];
}
cnt++;
return; // 回溯
}
// 遍历
// 当前(r, c) 遍历点(i, a[i])
for (int c = 1; c <= 8; ++c) { // 第 c 列
int flag = 1;
if (vis[c]) continue;
for (int i = 1; i < r; ++i) { // 遍历 1 ~ r-1 行
if (abs(r - i) == abs(c - a[i])) { // 左斜 / 右斜 已放置
flag = 0;
break;
}
}
if (flag) {
a[r] = c; // 更新
vis[c] = 1; // 标记
dfs(r + 1); // 递归
vis[c] = 0; // 取消标记
}
}
}
int main()
{
int T, n;
dfs(1); // 第一行开始
cin >> T;
while (T--) {
cin >> n;
cout << b[n] << endl; // 第 n 种答案
}
return 0;
}6
1
15863724
2
16837425
19
36271485
92
84136275
88
75316824
66
62713584
🌼三,P1605 迷宫
P1605 迷宫 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
标签:DFS,USACO,枚举,普及-


坑
记得标记起点已走过..............时隔一年再次做这道题,还是错在了这里....2024/2/2
强烈建议不会dfs的看看这个博客,里面的迷宫题模板,直接套在本题即可
(1条消息) 《啊哈算法》第四章之深度优先搜索_码龄?天的博客-CSDN博客
通过二维数组a[10][10]保存迷宫地图,障碍就a[i][j] = 1; 已走过的点就a[i][j] = -1,开始先初始化为a[i][j] = 0,表示都未走过
AC 代码
如果next数组声明为全局变量,会报错 the reference to next is ambiguous,因为next是C++标准库中一个函数,会产生命名冲突,所以,声明全局的话,next[][]改成dir[][]即可
#include<iostream>
using namespace std;
int a[10][10], ans = 0;
int sx, sy, fx, fy, n, m;
void dfs(int x, int y)
{
//到达目标
if(x == fx && y == fy) {
ans += 1;
return; //回溯
}
int next[4][2] = { //方向数组, 循环得到下一步坐标
{-1, 0}, //上
{1, 0}, //下
{0, -1}, //左
{0, 1}}; //右
//枚举四种走法
int tx, ty; //临时变量
for(int i = 0; i < 4; ++i) {
tx = x + next[i][0];
ty = y + next[i][1];
//判断越界
if(tx < 1 || ty < 1 || tx > n || ty > m)
continue; //换个方向
//不是陷阱且未走过
if(a[tx][ty] == 0) {
a[tx][ty] = -1; //标记走过
dfs(tx, ty); //递归
a[tx][ty] = 0; //取消标记
}
}
}
int main()
{
int t;
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
a[sx][sy] = -1; //标记初始走过
int h, y;
for(int i = 0; i < t; ++i) {
cin>>h>>y;
a[h][y] = 1; //1为障碍
}
dfs(sx, sy);
cout<<ans;
return 0;
}
🌼四,P1434 [SHOI2002] 滑雪
P1434 [SHOI2002] 滑雪 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
标签:搜索,递归,记忆化搜索,普及/提高-
一样的题,同样的代码能AC

这是一道20年前的省选题
这里采用记忆化dfs,听起来,记忆化,很高大上,实际上本题只多了2行代码。。。。。
总结就是dfs模板 + 2行代码
思路
第一次没用记忆化写了个void dfs,只AC了30%....
int dfs(int x, int y),然后声明全局二维数组Max[110][110]表示从该点出发的最大距离
由样例可知,初始点也算1距离,所以最后ans + 1
至于记忆化的2行呢,请看下面代码
int Max[110][110];
int dfs(int x, int y)
{
if(Max[x][y]) return Max[x][y];
}return Max[x][y],避免了重复计算,是不是有点像dp(动态规划)
题解👇
P1434 [SHOI2002] 滑雪 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
🌳AC 记忆化dfs
当然卡了好一会,看了别人题解才AC
解释下第20行,Max[x][y]表示(x, y)点出发的最大距离,Max[tx][ty]表示(tx, ty)出发的最大距离
由于(x, y) --> (tx, ty),所以后一个点距离+1,就等于前一个点可能的最大距离(利用前面已经保存的结果,就不用重新算一次已经算过的过程了)
#include<iostream>
using namespace std;
int Max[110][110], e[110][110]; //Max数组保存该点滑行距离
int n, m;
int nex[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //上下左右
//记忆化dfs类似DP
int dfs(int x, int y)
{
//关键: 记忆化dfs
if(Max[x][y]) return Max[x][y]; //已经得到的数据,就不用再算了
int tx, ty;
//遍历4个方向
for(int i = 0; i < 4; ++i) {
tx = x + nex[i][0];
ty = y + nex[i][1];
if(tx < 0 || ty < 0 || tx >= n || ty >= m)
continue;
if(e[x][y] > e[tx][ty]) {
dfs(tx, ty);
Max[x][y] = max(Max[x][y], Max[tx][ty] + 1); //这行也很关键
}
}
return Max[x][y];
}
int main()
{
cin>>n>>m;
//读入地图
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
cin>>e[i][j];
//dfs遍历
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
Max[i][j] = dfs(i, j);
//遍历Max数组得到最大长度
int num = 0;
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
num = max(num, Max[i][j]);
cout<<num + 1; //依题意加上初始点
return 0;
}洛谷上,不用记忆化,直接dfs能AC 90%
因为不熟练,我又在蓝桥杯官网敲了一次
AC 代码2
滑行 - 蓝桥云课 (lanqiao.cn)
#include<iostream>
using namespace std;
int Max[110][110], e[110][110];
int n, m, ans, nex[4][2] = {{1, 0},{-1,0},{0,1},{0,-1}};
int dfs(int x, int y)
{
if(Max[x][y]) return Max[x][y];
int tx, ty;
for(int i = 0; i < 4; ++i) {
tx = x + nex[i][0];
ty = y + nex[i][1];
if(tx < 0 || ty < 0 || tx >= n || ty >= m)
continue;
if(e[x][y] > e[tx][ty]) {
Max[x][y] = max(Max[x][y], dfs(tx, ty) + 1);
}
}
return Max[x][y];
}
int main()
{
cin>>n>>m;
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
cin>>e[i][j];
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
Max[i][j] = dfs(i, j);
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
ans = max(ans, Max[i][j]);
cout<<ans + 1;
return 0;
}🌼五,指数型枚举
92. 递归实现指数型枚举 - AcWing题库
标签:递归,简单


1~n个数,随机选取任意多个,那么每个数只有选和不选2种可能
所以方案数 = 2^n,单个方案n个数,那么时间复杂度 = O(2^15 * 15) ≈ 7.5 * 10^5
暴力没问题
因为输出数据达10^5以上,考虑printf(),提高速度
AC 代码1
1年后二刷,漏了空格,卡了半小时....2024/2/2
#include<iostream>
#include<cstdio> //printf()
using namespace std;
const int N = 20;
int n, vis[N]; //vis表示该位置是否选了
void dfs(int x) //x表示当前位置
{
if(x == n) { //到达边界
for(int i = 0; i < n; ++i) //从前往后遍历每一个
if(vis[i] == 1) //已选中
printf("%d ", i + 1);
printf("\n");
return; //不要忘记return
}
//选
vis[x] = 1; //标记选它
dfs(x + 1); //递归
vis[x] = 0; //取消标记
//不选
dfs(x + 1); //不选默认vis[x] == 0, 不需要处理
}
int main()
{
cin>>n;
dfs(0);
return 0;
}
4
1 2 3 4
1 2 3
1 2 4
1 2
1 3 4
1 3
1 4
1
2 3 4
2 3
2 4
2
3 4
3
4
补充知识点
1,
2的多少次方
“<<”是按位左移运算符,它会将某个二进制数向左移动指定的位数。例如,1 << 15表示将二进制数1向左移动15位,即:
0000000000000001 << 15 = 1000000000000000
所以,1 << 15在C++中表示的是二进制数1000000000000000
这个表达式可以用来快速计算2^15的值
具体来说,对于任意一个非负整数n,2^n可以表示为1左移n位,即1 << n
2,
puts("")相当于回车,puts相当于输出一个字符串 + 回车,当字符串为空,等价于只输出回车
AC 代码2
我们也可以把两个printf删掉,将所有方案用一个二维数组ways统计
#include<iostream>
#include<cstdio> //printf()
using namespace std;
const int N = 20;
int ways[1 << 15][16], cnt; //第cnt种方案
int n, vis[N]; //vis表示该位置是否选了
void dfs(int x) //x表示当前位置
{
if(x == n) { //到达边界
for(int i = 0; i < n; ++i) //从前往后遍历每一个
if(vis[i] == 1) //已选中
ways[cnt][i] = i + 1; //下标0开始,要加1
cnt++; //方案书 +1
return; //不要忘记return
}
//选
vis[x] = 1; //标记选它
dfs(x + 1); //递归
vis[x] = 0; //取消标记
//不选
dfs(x + 1); //不选默认vis[x] == 0, 不需要处理
}
int main()
{
cin>>n;
dfs(0);
//输出方案数
for(int i = 0; i < cnt; ++i) {
for(int j = 0; j < n; ++j) {
if(ways[i][j]) printf("%d ", ways[i][j]);
}
puts(""); //换行
}
return 0;
}
🌼六,排列型枚举
复杂度O(n * n!)
94. 递归实现排列型枚举 - AcWing题库
标签:简单,递归

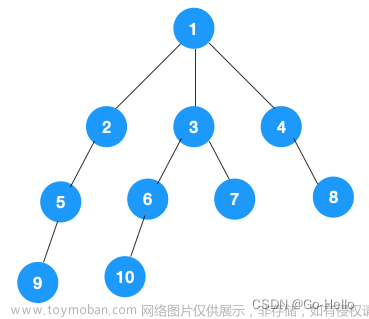
递归树👇辅助理解

我们采取枚举位置的方法,枚举位置x,再用for循环判断放第i个数
AC 代码
#include<iostream>
#include<cstdio> //printf()
using namespace std;
const int N = 10;
int n, vis[10], a[N];
void dfs(int x)
{
if(x == n + 1) { //边界
for(int i = 1; i <= n; ++i)
printf("%d ", a[i]);
puts(""); //换行
}
for(int i = 1; i <= n; ++i)
if(vis[i] == 0) { //数字i未选择
vis[i] = 1; //标记i已选择
a[x] = i; //数字i放入第x个坑
dfs(x + 1); //递归下一个位置
//恢复现场
//a[x] = 0; //这步不需要, 每一次开始前都会被覆盖
vis[i] = 0; //取消数字i的标记
}
}
int main()
{
cin>>n;
dfs(1); //第1个位置开始
return 0;
}
4
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1
🌼七,组合型枚举
93. 递归实现组合型枚举 - AcWing题库
组合型,只是比排列型,多了个限制条件,由于不能重复,也就是123 231 132等等默认是一种情况,我们可以要求后一个比前一个大
只需在for循环的 if 中加个判断
注意!代码第15 ~16行 if 的剪枝,没有也可以,但是会慢很多(100ms和1162ms的区别),剪枝,意思是不符合条件时终止后面的运算(具体时间差多少请看👇)
AC 代码
#include<iostream>
using namespace std;
const int maxn = 26;
int n, m, a[26];
void dfs(int step) //已选step个数字
{
if(step == m) {
for(int i = 0; i < m; ++i)
cout<<a[i]<<" ";
cout<<endl;
}
for(int i = 1; i <= n; ++i) {
if(n - i + 1 < m - step) //还需要选 m-step 个数字, 还能选 n-i+1 个数字
break; //剪枝, 表示剩余数字不够选了
if(!step || a[step - 1] < i) { //第一个数字默认可选; 上一个数字小于当前的 i
a[step] = i;
dfs(step + 1);
}
}
}
int main()
{
cin>>n>>m;
dfs(0);
return 0;
}🌼八,油田 Oil Deposits
标签:普及/提高-,DFS,连通块
油田 Oil Deposits - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
坑
void dfs()中,递归dfs(tx, ty);前,要加个判断 if(a[tx][ty] == '@'),否则,不是油田是不能走的,疏忽了
AC 代码1
直接修改 字符矩阵,a[][] = '*' 标记访问过
#include<iostream>
#include<cstring> //memset()
using namespace std;
int n, m;
char a[110][110];
void dfs(int x, int y)
{
a[x][y] = '*'; //标记
int dir[8][2] = {
{1,0},{-1,0},{0,1},{0,-1},{-1,1},{-1,-1},{1,1},{1,-1}
}; //8个方向
int tx, ty;
for(int i = 0; i < 8; ++i) {
tx = x + dir[i][0], ty = y + dir[i][1];
if(tx < 0 || ty < 0 || tx >= n || ty >= m)
continue;
if(a[tx][ty] == '@') //只有油田才能走
dfs(tx, ty);
//连通块不需要取消标记
}
}
int main()
{
while(cin>>n>>m) {
if(!n && !m) break;
int ans = 0;
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
cin>>a[i][j]; //读入油田
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
if(a[i][j] == '@') { //从一个点出发
ans++;
dfs(i, j); //遍历 -- 所有能到达的'@'标记为'*'
}
cout<<ans<<endl;
}
return 0;
}
AC 代码2
vis[][] = 1 标记走过
#include<iostream>
#include<cstring>
using namespace std;
int n, m, ans;
int vis[110][110];
char e[110][110]; // 存储地图
void dfs(int x, int y)
{
vis[x][y] = 1; // 标记
// 8 个方向
int dir[8][2] = {{1,0},{-1,0},{0,1},{0,-1},
{-1,1},{-1,-1},{1,1},{1,-1}};
for (int i = 0; i < 8; ++i) { // 遍历 4 个方向
// 新的坐标
int tx = x + dir[i][0], ty = y + dir[i][1];
if (tx < 0 || ty < 0 || tx >= n || ty >= m)
continue; // 越界
if (e[tx][ty] == '@' && !vis[tx][ty])
dfs(tx, ty); // 递归
}
}
int main()
{
while (cin >> n >> m) {
if (!n && !m) break;
ans = 0;
memset(vis, 0, sizeof(vis));
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
cin >> e[i][j]; // 读入
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if (e[i][j] == '@' && !vis[i][j]) {
dfs(i, j); // 对每一个未标记的油田dfs
ans++; // 每次dfs,会遍历一大片(8个方向邻接的所有油田)
}
cout << ans << endl;
}
return 0;
}🌼九,P1019 [NOIP2000 提高组] 单词接龙
标签:字符串,搜索,普及/提高-
P1019 [NOIP2000 提高组] 单词接龙 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
一道上古时代的题....(要注意的点挺多的,都在注释里)
解释1
具体解释下,main函数中,初始dfs()的传参👇
dfs(" "+s[n], 1);一开始,关于如何处理,用特定字符开头,挺苦恼的,所以采取这种方式传参
用样例举例
" "空格 + 字符串"a",当遇到 at,考虑到Link()函数中的dfs()递归👇
dfs(s[i], len_now + s[i].size() - k); //递归递归后的长度(即a 和 at 拼凑后的长度),就是 1 + 2 - 1 == 2,也就实现了给定字符开头
避免了开头的 a 因为被包含而被处理掉
解释2
题目原文“另外相邻的两部分不能存在包含关系,例如
at和atide间不能相连。”这里其实有歧义,不是不能包含,而是包含后长度必须增加,这里只可意会
AC 代码
#include<iostream>
using namespace std;
string s[30];
int use[30], ans, n; //use[]统计使用次数
int Link(string s1, string s2) //返回s1, s2最小重叠长度
{
int Min_len = min(s1.size(), s2.size());
for(int i = 1; i < Min_len; ++i) {//i 重叠长度
int flag = 1;
for(int j = 0; j < i; ++j) //j s2中下标
if(s1[s1.size() - i + j] != s2[j]) { //不匹配
flag = 0;
break;
}
if(flag) return i;
}
return 0; //最小重叠长度为0
}
void dfs(string now, int len_now) //len_now 拼凑后的长度
{
ans = max(ans, len_now); //更新答案
for(int i = 0; i < n; ++i) {
if(use[i] >= 2) continue; //已选2次, 不能再选了
int k = Link(now, s[i]); //后接s[i]的重叠长度
if(k) { //满足递归条件
use[i]++; //标记
dfs(s[i], len_now + s[i].size() - k); //递归
use[i]--; //取消标记
}
}
}
int main()
{
cin>>n;
for(int i = 0; i <= n; ++i)
cin>>s[i]; //读入字符串, s[n]为起始字符串
dfs(" "+s[n], 1);
cout<<ans;
return 0;
}
AC 代码2
时隔1年,回来二刷写的详解版本,对照着看
#include<iostream>
#include<cmath> // min()
using namespace std;
int ans, vis[30], n; // vis[] 记录每个单词只能用 2 次
string s[30];
// 返回 s1--s2 (最小)重叠长度
int Link(string s1, string s2)
{
int Min = min(s1.size(), s2.size());
// < Min 避免包含
for (int i = 1; i < Min; ++i) { // i 重叠长度
int flag = 1;
for (int j = 0; j < i; ++j) // j 字符串 s2 下标
// s1 从末尾开始,和 s2 开头对比
if (s1[s1.size() - i + j] != s2[j]) {
flag = 0; // 当前不匹配了
break;
}
if (flag) // 当前长度 i 匹配
return i;
}
return 0; // 重叠长度为 0
}
// now 尾巴字符串 both_len 拼凑后长度
void dfs(string now, int both_len)
{
ans = max(ans, both_len); // 更新最大长度
// 遍历
for (int i = 0; i < n; ++i) { // 新的字符串 s[i]
if (vis[i] >= 2) continue; // 最多使用 2 次
int k = Link(now, s[i]); // 后接 s[i] 的重叠长度
if (k) { // 存在重叠, 接龙后长度 up
vis[i]++; // 标记
dfs(s[i], both_len + s[i].size() - k); // 递归
vis[i]--; // 取消标记
}
}
}
int main()
{
cin >> n;
for (int i = 0; i <= n; ++i)
cin >> s[i]; // s[n] 即 龙头字母
// " " 防止龙头字母误判包含; 1 表示龙头字母长度
dfs(" " + s[n], 1);
cout << ans;
return 0;
}🍔总结
(一)n皇后,横 + 纵 + 主副对角线,用数组标记或找规律break
(二)迷宫,方向数组 + dfs模板,可在二维数组直接标记,注意传参(标记起点走过)
(三)滑雪,记忆化 + dfs模板,记忆化通过Max[][]避免重复搜索
(四)指数型枚举,1~n取任意个数,只有选 / 不选2种,将dfs模板for循环的遍历变成对2种情况的选择
(五)排列型枚举,全排列,dfs模板,画递归树辅助理解
(六)组合型枚举,1~n取m个数,dfs模板 + 限制条件(新取的数字要比上一个大),可剪枝(未选个数 < 待选个数 -- break)
(七)油田,连通块dfs,8个方向,对每个点dfs,将走过的点标记文章来源:https://www.toymoban.com/news/detail-843947.html(连通块,对每一个 dfs() 一次,所以不需要取消标记)只需在 dfs() 开头 标记
(八)单词接龙,(1)初始传参,dfs(" "+"...", 1)避免龙头字母被包含(2)Link()返回最小重叠长度(3)dfs() 遍历所有字符串文章来源地址https://www.toymoban.com/news/detail-843947.html
到了这里,关于DFS(深度优先搜索)8种题型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!