动态规划-背包问题-完全背包

这篇具有很好参考价值的文章主要介绍了动态规划-背包问题-完全背包。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

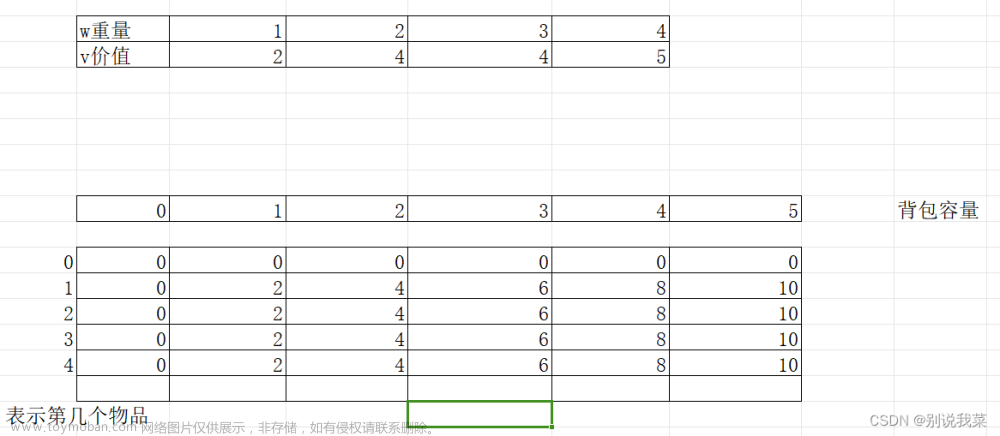
题目描述

对比01背包，完全背包中的每件物品有无数件。

也就是说，每件物品可以拿0，1，…，k，…件。

状态（和01背包一样）

dp[i][j]表示前i种物品，体积为j时的最大价值

状态转移

对于第i件物品：
- 不拿：dp[i][j]⇐dp[i-1][j]
- 拿一件：dp[i][j]⇐dp[i-1][j-w[i]]+v[i]
- 拿两件：dp[i][j]⇐dp[i-1][j-2w[i]]+2v[i]
- …
- 拿k件：dp[i]][j]⇐dp[i-1][j-kw[i]]+kv[i]

状态转移方程

$dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*w[i]]+k*w[i]),k=1,...,\frac{j}{w[i]}$
展开 $dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i],dp[i-1][j-2*w[i]]+2*v[i],...)(1+\frac{j}{w[i]}项)$
$dp[i][j-w[i]]=max(dp[i-1][j-w[i]],dp[i-1][j-2*w[i]]+*v[i],...)(\frac{j}{w[i]}项)$
综上可得dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i])
直观上理解为：前一项表示不取第i种，后一项表示在先前的基础上取第i种（取多次）

代码

n,V=map(int,input().split())
dp=[[0]*(V+1) for _ in range(n+1)]
for i in range(1,n+1):
    w,v=map(int,input().split())
    for j in range(V+1):
        if j<w:
            dp[i][j]=dp[i-1][j]
        else:
            dp[i][j]=max(dp[i-1][j],dp[i][j-w]+v)
print(dp[n][V])

滚动数组优化

		…	i-1,j
	i,j-w[i]		i,j

可见，更新dp[i][j]时，用的是同一行先前位置dp[i][j-w[i]]和上一行对应位置的dp[i-1][j]，和01数组不同在于更新方向。

使用单个数组更新时，采用从小到大的方向对dp数组进行覆盖。文章来源地址https://www.toymoban.com/news/detail-844506.html

n,V=map(int,input().split())
dp=[0]*(V+1) 
for i in range(1,n+1):
    w,v=map(int,input().split())
    for j in range(w,V+1):
        dp[j]=max(dp[j],dp[j-w]+v)
print(dp[V])