1. Toy模板网首页
  2. > Toy博客

数据结构与算法——排序（C语言实现）

7月前 作者：悦心无谓 分类：Toy博客 阅读(54) 违法举报

这篇具有很好参考价值的文章主要介绍了数据结构与算法——排序（C语言实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌟🌟 追风赶月莫停留 🌟🌟
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
🌟🌟 平芜尽处是春山🌟🌟
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅

🍑插入排序

🍍直接插入排序

#include<stdio.h>
/// 直接插入排序
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 2; i++)
	{
		int end = i;
		int cur = a[end + 1];
		while (cur >= 0)
		{
			if (cur < a[end])
			{
				a[end + 1] = a[end];
			}
			else
			{
				break;
			}
			end--;
		}
		a[end + 1] = cur;
	}
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	InsertSort(a, size);
	for (int i = 0; i < size; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

0到end有序，把end+1序列插入到前序序列
控制[end + 1]序列有序

直接插入排序有点类似尾插，都是从后面开始往前比较，和我们平常打扑克洗牌类似。

🍍希尔排序

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//保证了gap最小为1
		for (int i = 0; i < n - gap; i = i + gap)
		{
			int end = i;
			int cur = a[end + gap];
			while (end >= 0)
			{
				if (cur < a[end])
				{
					a[end + gap] = a[end];
				}
				else
				{
					break;
				}
				end = end - gap;
			}
			a[end + gap] = cur;
		}
	}
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	ShellSort(a, size);
	for (int i = 0; i < size; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

该排序就是：预排序加直接插入排序

gap的作用就是分成多少组，一组一组的排

预排序的作用就是让大的数更快的到后面去，而小的数更快的到前面来
在这里gap等于1的时候就是直接插入排序

🍑选择排序

🍍选择排序

void Swap(int* a1, int* a2)
{
	int cur = *a1;
	*a1 = *a2;
	*a2 = cur;
}
void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int max = begin;
		int min = begin;
		for (int i = begin+1; i <= end; i++)
		{
			if (a[i] < a[min])
			{
				min = i;
			}
			if (a[i] > a[max])
			{
				max = i;
			}
		}
		Swap(&a[begin], &a[min]);
		if (max == begin)//特殊情况
		{
			max = min;
		}
		Swap(&a[max], &a[end]);
		begin++;
		end--;
	}
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	SelectSort(a, size);
	Print(a, size);

	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

图里就简单列出了三步，帮大家理清程序的逻辑。

选择排序就是从一堆数里选出最大和最小，然后最大的放在最右边，最小的放在最左边，然后在有效的数据长度里不断执行这一步就可以了。

然而还有一种特殊情况：

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
在图中，最大的数恰好是在begin位置上，我们程序上是先把最小的放到最左边，此时a[min]和a[begin]就会互换位置，如下：

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

此时max上的数已经不是最大的了，接下来再把最大的数放在最右边，就出错了，所以在这里我们就需要加一个判断：

if (max == begin)//特殊情况
		{
			max = min;
		}

大家可能还有疑问，我们这里的执行顺序是先把最小的数放在最左边，然后把最大的数放在最右边。

有的人肯定就会问如果先执行把最大的数放在最右边，再执行把最小的数放在最左边，这样是不是就不会出现这种特殊情况了。

但我想说的是，如果此时最小的数恰好在end上呢，两种都是特殊的情况，而且类似。

🍍堆排序

此处排序请看上篇博客：堆和二叉树的动态实现（C语言实现）,这篇博客详细的介绍了堆排序。

🍑交换排序

🍍冒泡排序

void Swap(int* a1, int* a2)
{
	int cur = *a1;
	*a1 = *a2;
	*a2 = cur;
}

void BuddleSort(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
			}
		}
	}
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	BuddleSort(a, size);
	for (int i = 0; i < size; i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

冒泡排序大家应该熟悉，这个排序就是两个两个的比较，从第一个一直比到后面。这个冒泡排序是最基础的排序。

🍍快速排序

🍌快排（经典写法）

void Swap(int* a1, int* a2)
{
	int cur = *a1;
	*a1 = *a2;
	*a2 = cur;
}
int PartSort1(int* a, int left, int right)//单趟
{
	int key = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[key]);
	return left;
}

void QuickSort1(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = PartSort1(a, left, right);
	QuickSort1(a, left, key - 1);
	QuickSort1(a, key + 1, right);
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	QuickSort1(a, 0, size - 1);
	Print(a, size);

	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
上图中就是单趟的走法。

在单趟走法中有几个坑：
（1）第一个坑就是在第一个while循环中有left<right了有的人就认为在while程序内部就会一直维持left<right，其实是错的。在单趟的走法中，无论是right往右走，还是left往左走，都有可能left>right发生。
（2）第二个坑就是在判断条件a[key]>=a[right]或者a[key]<=a[left]中，等号可不可以去掉。在这里可以肯定的是这个等号是不可以去掉的，去掉的话会陷入无限循环中。

在这个排序中，我们还是利用了二叉树的知识点，先从左子树排序，然后再是右子树，当然基础都是利用了递归。

如果有需要了解二叉树的知识可以查看这篇博客：堆和二叉树的动态实现（C语言实现）,这篇博客详细的介绍了堆排序。

🍌快排（挖坑法）

int PartSort2(int* a, int left, int right)
{
	int key = a[left];
	int hold = left;
	while (left < right)
	{
		//找小
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hold] = a[right];
		hold = right;
		//找大
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hold] = a[left];
		hold = left;
	}
	a[hold] = key;
	return hold;
}


void QuickSort2(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = PartSort2(a, left, right);
	QuickSort2(a, left, key - 1);
	QuickSort2(a, key + 1, right);
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	QuickSort1(a, 0, size - 1);
	Print(a, size);

	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
快排（挖坑法）这是比较好理解。其中需要注意的和上面的差不多。

🍌快排（双指针法）

void Swap(int* a1, int* a2)
{
	int cur = *a1;
	*a1 = *a2;
	*a2 = cur;
}
int PartSort3(int* a, int left, int right)
{
	int key = left;
	int cur = left + 1;
	int old = left;
	while (cur <= right)
	{
		if (a[cur] <= a[key])
		{
			old++;
			Swap(&a[old], &a[cur]);
		}
		cur++;
	}
	Swap(&a[key], &a[old]);
	return old;
}

void QuickSort3(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = PartSort3(a, left, right);
	QuickSort3(a, left, key - 1);
	QuickSort3(a, key + 1, right);
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);
	QuickSort3(a, 0, size - 1);
	Print(a, size);

	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
这个双指针写法，明显比上面的两种都好理解，代码也简单些。这个想法还是如果a[cur]比key大，就光cur++。如果a[cur]比key小，就先old++,再把a[cur]赋给a[old]，然后cur++。整体的思路就是这些。

🍌快排优化

上面我们介绍了三种快排的写法，其中我们在取key值的时候都是取left，left一开始都是代表最左边的数据，而在现实，left代表的值的大小不一定是在中间，如果left代表的值是较小的或者是较大的那么可能对于快排相较于其它排序来说，此种情况就是快排最坏的情况，可能比堆排或则希尔排序等来说还要慢。

所以在取key值的时候加了一个三数取中的程序：

// 三数取中
int GetMiddle(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	// left mid right
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])  // mid是最大值
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right]) // mid是最小
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

这个程序就是简单的取一个中间数的大小，这样快排就不会出现上面所讲的那种情况。

🍑归并排序

🍍归并排序（递归）

void _MergeSort(int* a, int *tem, int left, int right)
{

	//递归
	if (right <= left)
		return;
	int mid = (left + right) / 2;
	_MergeSort(a, tem, left, mid);
	_MergeSort(a, tem, mid+1, right);

	//归并，拷贝到tem中
	int left1 = left, right1 = mid;
	int left2 = mid + 1, right2 = right;
	int sum = left;
	while (left1 <= right1 && left2 <= right2)
	{
		if (a[left1] < a[left2])
		{
			tem[sum++] = a[left1++];
		}
		else
		{
			tem[sum++] = a[left2++];
		}
	}

	while (left1 <= right1)
	{
		tem[sum++] = a[left1++];
	}

	while (left2 <= right2)
	{
		tem[sum++] = a[left2++];
	}

	memcpy(a + left, tem + left, (right - left + 1) * sizeof(int));

}

void MergeSort(int* a, int n)
{
	int* tem = (int*)malloc(sizeof(int) * n);
	if (tem == NULL)
	{
		perror("malloc  fail");
		return;
	}

	_MergeSort(a, tem, 0, n - 1);

	free(tem);
}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456 };
	int size = sizeof(a) / sizeof(a[0]);

	MergeSort(a, size);
	Print(a, size);
	return 0;
}

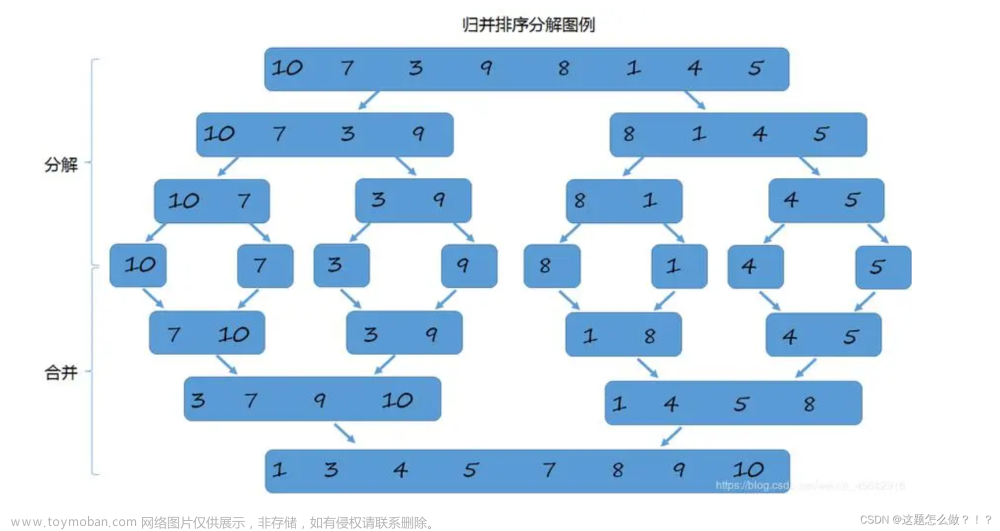
该种排序是利用递归实现的。

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
具体的流程如上面图中所示。大概就是分为六步，完成后在把数组拷贝回原来数组就可以了

🍍归并排序（非递归）

void Print(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}


void MergeSortNort(int* a, int n)
{
	int* cur = (int*)malloc(n * sizeof(int));
	if (cur == NULL)
	{
		perror("malloc  fail");
		return;
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i = i + 2 * gap)
		{
			int left1 = i, right1 = i + gap - 1;
			int left2 = i + gap, right2 = i + 2 * gap - 1;
			int sum = i;
			while (left1 <= right1 && left2 <= right2)
			{
				if (a[left1] < a[left2])
				{
					cur[sum++] = a[left1++];
				}
				else
				{
					cur[sum++] = a[left2++];
				}
			}

			while (left1 <= right1)
			{
				cur[sum++] = a[left1++];
			}
			while (left2 <= right2)
			{
				cur[sum++] = a[left2++];
			}

			memcpy(a + i, cur + i, (2 * gap) * sizeof(int));
		}
		//printf("\n");
		gap = gap * 2;
	}


}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456, };
	int size = sizeof(a) / sizeof(a[0]);
	MergeSortNort(a, size);

	Print(a, size);
	return 0;
}

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

程序的逻辑就是图中一步一步的来，和递归的执行过程有些部分是相似的，就是在这里，空间的区分可能难以让人理解，大家可以代数进去尝试，多凭自己的想法写几遍，大致过程也就心里有数了。

大家在图中也看到了，最后gap取的是偶数，所以这个程序的前提条件就是数据只能是偶数次的数据，而一旦是奇数程序就会报错。接下来有一个修正版，大家可以先把偶数版的理解了，再去看奇数版的会轻松很多。

如果数据个数是偶数：
数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

这里区间一切正常，也成功排序。

如果数据个数是奇数：

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

从图中可知，标的有箭头的区间划分中，都超出范围了，所以我们有必要修正

归并排序优化：

void Print(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}


void MergeSortNort(int* a, int n)
{
	int* cur = (int*)malloc(n * sizeof(int));
	if (cur == NULL)
	{
		perror("malloc  fail");
		return;
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i = i + 2 * gap)
		{
			int left1 = i, right1 = i + gap - 1;
			int left2 = i + gap, right2 = i + 2 * gap - 1;
			printf("[%d  %d]  [%d  %d]\n", left1, right1, left2, right2);
			//如果第二组不存在，这一组就不用归并
			if (left2 >= n)
			{
				break;
			}
			//如果第二组右边见越界了，就修正一下
			if (right2 >= n)
			{
				right2 = n - 1;
			}

			int sum = i;
			while (left1 <= right1 && left2 <= right2)
			{
				if (a[left1] < a[left2])
				{
					cur[sum++] = a[left1++];
				}
				else
				{
					cur[sum++] = a[left2++];
				}
			}

			while (left1 <= right1)
			{
				cur[sum++] = a[left1++];
			}
			while (left2 <= right2)
			{
				cur[sum++] = a[left2++];
			}

			memcpy(a + i, cur + i, (right2 - i + 1) * sizeof(int));
		}
		gap = gap * 2;
	}


}

int main()
{
	int a[] = { 2,66,34,5,123,34,345,456, 3};
	int size = sizeof(a) / sizeof(a[0]);
	MergeSortNort(a, size);

	Print(a, size);
	return 0;
}

修正后的程序，主要增加了2个判断和修改了范围。

两个判断：数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序
第一个判断是防止第二组区间不存在，就直接结束，如：

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

当然有的人就会问，在这个图中第一个区间的right2不是也超了吗，为什么不要判断right1呢？

大家可以试着想一想，如果right2超过了区间范围，left2是不是有可能也超过了范围。而left2超出范围了,right1是不是一定超出了范围。这就是一个谁先谁后的问题。大家可以仔细想一想，可以代数进去尝试一下。而且你判断了left2超出区间了，程序就已经跳出循环了。

第二个判断：

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序

就是right2超出了区间范围，而left2没有超出，只需要把right2修正到有效范围就可以了，如上图所示，只需要把15修正成8，就可以了。

今天排序的知识点就得差不多了，本人水平有限，可以知识点尚未完全覆盖，请大家多多指教，谢谢！！！！！！！

数据结构与算法——排序（C语言实现）,数据结构与算法,c语言,排序算法,开发语言,数据结构,算法,排序文章来源地址https://www.toymoban.com/news/detail-844822.html

到了这里，关于数据结构与算法——排序（C语言实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【数据结构与算法】JavaScript实现排序算法

    【数据结构与算法】JavaScript实现排序算法

    一、大O表示法 大O表示法： 在计算机中采用 粗略的度量 来描述计算机算法的 效率 ，这种方法被称为 “大O”表示法 在 数据项个数 发生改变时， 算法的效率 也会跟着改变。所以说算法A比算法B快两倍，这样的比较是 没有意义 的。 因此我们通常使用 算法的速度 随着 数据

    2024年02月02日
    浏览(48)
  • 【数据结构与算法】归并排序详解：归并排序算法，归并排序非递归实现

    【数据结构与算法】归并排序详解：归并排序算法，归并排序非递归实现

    归并排序是一种经典的排序算法，它使用了分治法的思想。下面是归并排序的算法思想： 递归地将数组划分成较小的子数组，直到每个子数组的长度为1或者0。 将相邻的子数组合并，形成更大的已排序的数组，直到最终得到一个完全排序的数组。 归并排序的过程可以分为三

    2024年01月22日
    浏览(66)
  • 【数据结构与算法】：非递归实现快速排序、归并排序

    【数据结构与算法】：非递归实现快速排序、归并排序

    🔥 个人主页 ： Quitecoder 🔥 专栏 ：数据结构与算法 上篇文章我们详细讲解了递归版本的快速排序，本篇我们来探究非递归实现快速排序和归并排序 快速排序的非递归实现主要依赖于栈（stack）来模拟递归过程中的函数调用栈。递归版本的快速排序通过递归调用自身来处理子

    2024年03月24日
    浏览(52)
  • 【数据结构与算法C++实现】3、排序算法

    【数据结构与算法C++实现】3、排序算法

    原视频为左程云的B站教学 外层循环 ：n个数需要冒n-1个泡上去，剩下的一个必然是最小的。所以外层循环执行n-1轮 内层循环 ：比大小，第1个泡需要比n-1次，第2个泡,比较n-2次… 选择： 每次从待排序序列中选择 最小的一个 放在已排序序列的后一个位置 原理类似于对扑克牌

    2024年02月11日
    浏览(56)
  • 常见排序集锦-C语言实现数据结构

    常见排序集锦-C语言实现数据结构

    目录 排序的概念 常见排序集锦      1.直接插入排序      2.希尔排序      3.选择排序      4.堆排序      5.冒泡排序      6.快速排序             hoare              挖坑法             前后指针法             非递归      7.归并排序             非递归 排序实现

    2024年02月12日
    浏览(46)
  • 【数据结构】用Java实现七大排序算法

    【数据结构】用Java实现七大排序算法

    目录 🌷1. 排序的概念及引用 1.1 排序的概念 1.2 衡量指标 1.2 十个排序算法  1.3 十个排序性能对比 🌷2. 冒泡排序 2.1 算法描述 2.2 动图 ⭐️代码优化 🌷3. 选择排序 3.1 算法描述 3.2 动图  3.3 代码 🌷4. 插入排序 4.1 算法描述 4.2 动图  4.3 代码 🌷5 希尔排序 5.1 描述 5.2 动图  

    2023年04月23日
    浏览(49)
  • 数据结构——C语言实现常见排序(插入排序、希尔排序、选择排序、堆排序、冒泡排序)

    数据结构——C语言实现常见排序(插入排序、希尔排序、选择排序、堆排序、冒泡排序)

    现在是北京时间2023年6月23日13点19分，度过了一个非常愉快的端午节。由于刚从学校回家，一下子伙食强度直升了个两三个档次。这也导致我的肠胃不堪重负，我也准备等会去健身房消耗一下盈余的热量。回到家陪伴爷爷走人生最后的阶段才是我这个暑假最重要的事情。自从

    2024年02月10日
    浏览(49)
  • [数据结构 -- 手撕排序算法第七篇] 递归实现归并排序

    [数据结构 -- 手撕排序算法第七篇] 递归实现归并排序

    目录 1、归并的思想 2、归并排序的思想 2.1 基本思想 2.2 图解分析 3、归并排序递归版本代码实现 3.1 代码解析 3.2 注意事项 3.2.1错误划分：[begin, mid-1]，[mid, end] 3.2.2 正确划分：[begin, mid], [mid+1, end] 4、归并排序的测试 5、时间复杂度、空间复杂度分析 5.1 时间复杂度 5.2 空间复杂

    2024年02月16日
    浏览(45)
  • 【算法与数据结构】Java实现查找与排序

    【算法与数据结构】Java实现查找与排序

    也叫做折半查找，属于有序查找算法。 前提条件 ：数组数据必须有序，从小到大，或者从大到小都是可以的。 如果是无序的，也可以先进行排序。 但是排序之后，会改变原有数据的顺序，查找出来元素位置跟原来的元素可能是不一样的，所以排序之后再查找只能判断当前数

    2024年01月19日
    浏览(46)
  • 【数据结构】—从冒泡排序丝滑过度快速排序（含C语言实现）

    【数据结构】—从冒泡排序丝滑过度快速排序（含C语言实现）

                                            食用指南：本文在有C基础的情况下食用更佳                                          🔥 这就不得不推荐此专栏了： C语言                                        ♈️ 今日夜电波：靴の花火—ヨルシカ            

    2024年02月08日
    浏览(38)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包