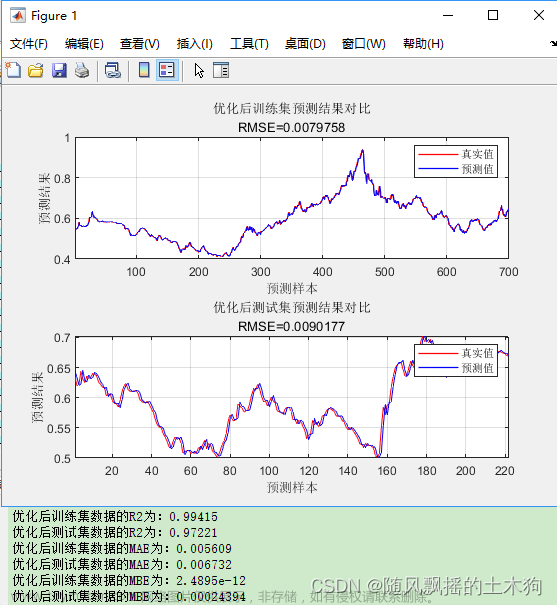
一、什么是高斯过程回归,他是用来干什么的
高斯过程回归是一种监督学习方法,我们可以将回归理解为拟合,比如:线性拟合,就是将一些数据拟合成一条直线。那么高斯过程回归就是将数据拟合成高斯过程,进而实现预测。
举个例子:我们在同一地点从上午八点开始,每隔一个小时采集一次气温,直至下午五点结束。那么我们可以用采集到的气温信息,拟合成高斯过程去预测一个小时之后的气温。
再举个例子:我们在同一时间内,在不同的地方采集气温,我们可以通过这些数据,拟合成高斯过程去预测当前时刻其他地方的气温。
值得注意的是!!!高斯过程不是简单的高斯分布。我们首先简单介绍一下高斯过程。
二、高斯过程
高斯过程是连续域(例如空间域和时间域)上无线多个点的联合高斯分布。
对于一维高斯分布,我们可以用该数据的均值和该数据的方差来表示,
对于二维高斯分布,我们可以用这两个数据的均值和他们之间的协方差矩阵来表示,,其中,为协方差矩阵。
对于连续域上无数个多维高斯分布(以空间域为例),我们用空间上的每个点的均值和这些点之间的协方差矩阵来表示这个无限维的高斯分布,即高斯过程。此时,均值和协方差矩阵就由原来的单个数字,变成了函数,即均值函数和协方差函数。
其中,表示第个点的坐标,为均值函数;表示协方差函数。
因此,我们只需要均值函数和协方差矩阵函数即可确定一个高斯过程。并且一个高斯过程的有限维度的子集都服从一个多元高斯分布。
三、高斯过程回归
我们以空间域为例进行解释,假设空间中第i个点的坐标为,该点的数据输出为,则高斯过程回归模型的表达式为:
其中表示噪声变量,服从。在GPR中,我们假设服从高斯过程,即:
其中,m(x)为均值函数,K(x,x')为协方差函数,我们也称之为核函数。
四、给出均值函数和核函数
我们已经假设服从高斯过程,同时,高斯过程是由一个均值函数和一个协方差函数来确定的,那么为了对进行表示,我们需要给出均值函数和协方差函数
通常来讲,我们将均值函数设为0。为什么会设为零呢,这显然不符合常识,特别是对于那些已经通过测量而得到数据输出的点来说,那些点的均值应该是测量值的均值才对。
首先,均值函数设为0是为了方便计算,可以简化我们的公式。
其次,均值函数设为0,即便他有些不符合“常识”,但对于短期预测结果来说几乎没有影响,均值函数影响的是长期预测结果,举个例子:你在某一时刻测量了南京新街口50米×50米范围内多个点的气温,你想通过这些测量值去预测距离测量范围1米处的气温,此时均值函数的影响很小;但如果你想预测北京某地的气温,那预测值几乎等于均值函数值,然而,这样的预测是不准确的。
最后,这里的均值函数和协方差函数可以理解为先验概率,也就是说对于“地点—气温”这一函数,给出的先验概率是怎样的,如果有确定的函数关系,则可以将这个函数作为均值函数。如果没有,则通常设为0。
协方差函数,也就是核函数,在这里极其重要。核函数是高斯过程的核心,它决定了高斯过程的性质。不同的核函数得到的高斯过程性质也不一样。
比较常用的核函数是高斯核函数,也就是径向基函数RBF。其基本形式如下:
在上式中,和是需要人为给定的参数,我们称之为超参数。通常会根据采集到的数据对超参数进行简单的计算,根据计算得到的超参数给出核函数。
五、基于高斯过程回归的预测
我们给出了高斯过程回归的模型表达式:
以及高斯过程的均值函数和协方差矩阵函数:
其中,
现在我们根据高斯过程回归进行预测。设和为数据库中已有的位置坐标及其对应的数据值。和为预测点的位置坐标及其对应的数据值。因为服从高斯过程,那么和服从联合高斯分布,即
通过贝叶斯公式,得到的概率分布。
p的计算过程即为舒尔补求解,我会在文章最后给出舒尔补的求解过程。
将均值函数和协方差函数代入,即可得到预测点的概率表达式。
需要注意的是,我们一直假设的是f(x)服从高斯过程,在函数的输出y中,还有一个噪声项。
我们将噪声项加入其中,并重新给出公式。
六、根据已有数据给出超参数
在上文中,需要人为给定的超参数实际上有三个,。
分别是高斯过程表达式和核函数中的超参数,我们统一用表示。
我们需要让构建的高斯过程表达式,能够准确的表达坐标点x和数据输出y之间的关系,因此,我们应当找到一组超参数使得y的似然估计最大。
至此,标准高斯过程回归全部结束。
附录 舒尔补公式推导
多元高斯分布的概率密度函数为:
假设一对多元正态分布变量(x,y),他们的联合概率密度函数:
其中,我们的目的是将联合密度分解为条件概率和边缘概率的乘积,即
首先,我们可以将协方差矩阵进行分解:
对矩阵两边进行求逆运算:
将联合概率密度p(x,y)的指数部分二次项展开,可以得到:
由于幂运算中同底数幂相乘,底数不变,指数相加的性质,可以得到:文章来源:https://www.toymoban.com/news/detail-844877.html
文章来源地址https://www.toymoban.com/news/detail-844877.html
到了这里,关于标准高斯过程回归(Gaussian Processes Regression, GPR)从零开始,公式推导的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!