自相关算法,协方差算法,后向加窗算法,前向加窗算法以及QR分解法的理论介绍与matlab仿真分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了自相关算法,协方差算法,后向加窗算法,前向加窗算法以及QR分解法的理论介绍与matlab仿真分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.自相关算法

2.协方差算法

3.后向加窗算法

4.前向加窗算法

5.QR分解法

1.自相关算法

自相关算法是一种在信号处理中用来描述信号特性的算法，它主要用于估计一个信号的功率谱。对于一个离散信号x[n]，其自相关函数定义为：

Rxx[n] = E[x[n+m]*x[m]]

其中E[]表示期望。可以看出，自相关函数描述了信号在其时间延迟n+m点处的强度与在m点处的强度之间的相关性。

将自相关函数以复数形式表示，并对其进行傅里叶变换，即可得到信号的功率谱。具体来说，离散信号x[n]的自相关函数为Rxx[n]=x[n]x[0]、x[n]x[1]、…、x[n]x[N-1]，其中N为信号长度。对Rxx[n]进行傅里叶变换得到X(w)=∑n=-∞∞Rxx(n)e-jwn，即可得到信号的功率谱X(w)。

因此，自相关算法的原理是利用信号的自相关函数来描述信号的特性，并通过傅里叶变换得到信号的功率谱。数学公式为：

X(w) = ∑n=-∞∞Rxx(n)e-jwn

h=zeros(1,M);
Acovariance=[;;];
for i=M:N;
   for j=1:M
   Acovariance(i-M+1,j)=A(i,j);
    end
end
AHcovariance=Acovariance';
d=[];
for i=M:N
 d(i+1-M)=x(i)-vn(i);
end
h=inv(AHcovariance*Acovariance)*AHcovariance*d';
xLSc=conv(x,h);

测试结果如下：

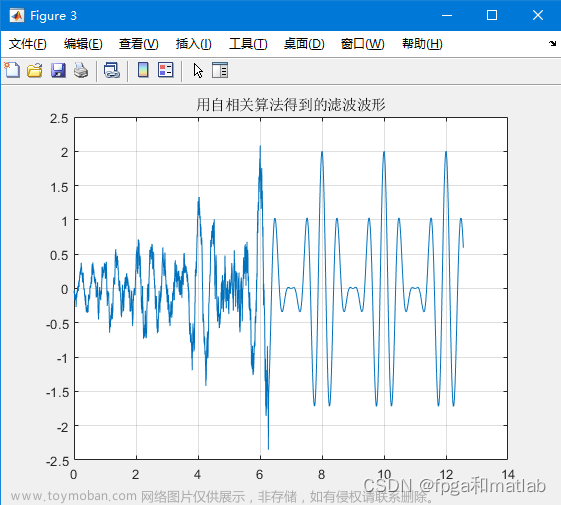
自相关数学公式,MATLAB,板块1:通信与信号处理,matlab,自相关算法,协方差算法,后向加窗算法,前向加窗算法,QR分解法

2.协方差算法

协方差算法是一种用于衡量两个随机变量之间关系的方法。它的基本思想是通过对两个随机变量进行减均值、乘积和求和的方式来得到一个衡量它们之间关系的数值，即协方差。

具体来说，设X和Y是两个随机变量，μX和μY分别是它们的均值。我们可以将X和Y的减均值、乘积和求和写成如下形式：
cov(X,Y)=Σ(X-μX)(Y-μY)/n
其中n是样本数量。在这个公式中，(X-μX)和(Y-μY)分别表示X和Y与各自均值的差，它们的乘积表示这两个差值的乘积，求和则是将这些乘积相加。

从数学角度来看，协方差是两个随机变量的偏差乘积的总和除以样本数量。这个数值可以反映两个变量之间的相关性，即它们在多大程度上呈现出一致或相反的变化趋势。如果协方差的值为正，说明两个变量呈现出一致的变化趋势；如果协方差的值为负，则说明它们呈现出相反的变化趋势；如果协方差的值为零，则说明两个变量之间没有相关性。

除了计算协方差之外，我们还可以通过协方差矩阵来描述多个随机变量之间的关系。在这种情况下，协方差矩阵中的每个元素都表示两个随机变量之间的协方差。

hs=zeros(1,M);
Aselfcorrelation=A;
ds=zeros(1,N+M-1);
for i=1:N
    ds(i)=x(i)-vn(i);
end
AHselfcorrelation=Aselfcorrelation';
hs=inv(AHselfcorrelation*Aselfcorrelation)*AHselfcorrelation*ds';
xLSs=conv(x,hs);

测试结果如下：

3.后向加窗算法

后向加窗算法是一种在信号处理中对数据进行加窗处理的方法，目的是在不改变信号的频谱特性的情况下，降低信号的时间分辨率。这种算法与前向加窗算法类似，但是它是将窗函数应用到信号的尾端。

对于长度为N的信号x[n]，其后向加窗函数定义为：
w[n] = 1(0 ≤ n ≤ N-1)w_N = \begin{cases}w[N-1] & \text { for } n=0 \ w[n-1] & \text { for } 1 \leq n \leq N-1\end{cases}其中w[N-1]表示窗函数的最后一个值，w[n-1]表示窗函数在当前位置向左偏移一位的值。这样，通过应用后向加窗函数，可以将原本连续的信号x[n]分成长度为N的段，每段信号都被窗函数所限制，从而降低了信号的时间分辨率。

需要注意的是，在应用后向加窗算法时，需要对信号的长度和窗函数的长度进行匹配。一般来说，窗函数的长度应该远小于信号的长度，这样才能保证窗函数对信号的影响是局部的，避免对信号的整体特性造成大的影响。

后向加窗算法的数学公式如下：
x_w(n)=w(n)x(n), n=0,1,2,...,N-1x_w(n)=w(n)x(n)=wx(n)=0,1,2,...,N-1其中x_w(n)表示加窗后的信号，w(n)表示窗函数，x(n)表示原始信号。

总之，后向加窗算法是一种在信号处理中对数据进行加窗处理的方法，它可以降低信号的时间分辨率，而不会对信号的频谱特性产生大的影响。

hba=zeros(1,M);
dba=zeros(1,N);
Abaw=[;;];
for i=M:N+M-1
    for j=1:M
        Abaw(i-M+1,j)=A(i,j);
    end
end
AHbaw=Abaw';
for i=M:N
    dba(i-M+1)=yn(i);
end
hba=inv(AHbaw*Abaw)*AHbaw*dba';
xLSba=conv(hba,x);

测试结果如下：

4.前向加窗算法

前向加窗算法是一种在信号处理中对数据进行加窗处理的方法，目的是在不改变信号的频谱特性的情况下，降低信号的频谱分辨率。这种算法与后向加窗算法类似，但是它是将窗函数应用到信号的起始端。

需要注意的是，在应用前向加窗算法时，需要对信号的长度和窗函数的长度进行匹配。一般来说，窗函数的长度应该远小于信号的长度，这样才能保证窗函数对信号的影响是局部的，避免对信号的整体特性造成大的影响。

前向加窗算法的数学公式如下：
x_w(n)=w(n)x(n), n=0,1,2,...,N-1x_w(n)=w(n)x(n)=wx(n)=0,1,2,...,N-1

其中x_w(n)表示加窗后的信号，w(n)表示窗函数，x(n)表示原始信号。

总之，前向加窗算法是一种在信号处理中对数据进行加窗处理的方法，它可以降低信号的频谱分辨率，而不会对信号的频谱特性产生大的影响。

hfa=zeros(1,M);
dfa=[];
Afaw=[;;];
for i=1:N
    for j=1:M
        Afaw(i,j)=A(i,j);
    end
end
AHfaw=Afaw';
for i=1:N
    dfa(i)=yn(i);
end
hfa=inv(AHfaw*Afaw)*AHfaw*dfa';
xLSfa=conv(hfa,x);

测试结果如下：

5.QR分解法

QR分解法是一种求一般矩阵全部特征值的最有效并广泛应用的方法。这种方法的基本思路是将一个矩阵分解为一个正交矩阵和一个上三角矩阵的乘积。

具体来说，对于一个m×n的矩阵A，存在一个正交矩阵Q和一个上三角矩阵R，使得A=QR。这里的Q是一个m×m的正交矩阵，R是一个m×n的上三角矩阵。正交矩阵的列向量相互正交，即QTQ=QQT=I，I是单位矩阵。上三角矩阵的特点是主对角线上的元素是矩阵的主要特征值，其他元素为0。

在QR分解法中，首先将一个矩阵经过正交相似变化成为Hessenberg矩阵。这个过程可以通过一系列行和列的初等行变换和列变换实现。然后，应用QR方法求出Hessenberg矩阵的特征值和特征向量。这个过程包括对Hessenberg矩阵进行一系列的QR分解和重构，直到得到最终的特征值和特征向量。

数学公式如下：
A=QR其中Q是一个正交矩阵，R是一个上三角矩阵。

总之，QR分解法是一种求一般矩阵全部特征值的有效方法，它通过将矩阵分解为正交矩阵和上三角矩阵的乘积来实现对矩阵特征值的求解。

[Q,R]=qr(Afaw);
Rfa=[;;];
Qfa=[;;];
for i=1:M
    for j=1:M
        Rfa(i,j)=R(i,j);
    end
end
for i=1:N;
    for j=1:M
        Qfa(i,j)=Q(i,j);
    end
end
QHfa=Qfa';
zfa=QHfa*yn';
hQRfa=inv(Rfa)*zfa;
xLSQRfa=conv(hQRfa,x);

测试结果如下：

自相关数学公式,MATLAB,板块1:通信与信号处理,matlab,自相关算法,协方差算法,后向加窗算法,前向加窗算法,QR分解法文章来源地址https://www.toymoban.com/news/detail-845639.html