动态规划的几个经典问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划的几个经典问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

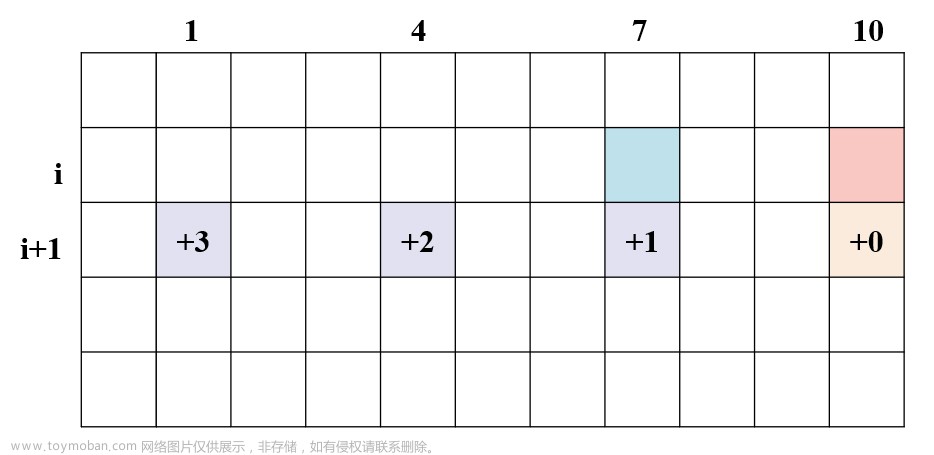
矩阵链加括号问题

【问题描述】给定n个矩阵A1, A2 ,…, An, 其中Ai与Ai+1是可乘的, 计算这n个矩阵的连乘积A1A2…An。用加括号的方法表示矩阵连乘的次序。

【输入形式】

输入有2行，第1行输入一个整数n，第2行输入n个矩阵的维度值p0,p1,...,pn

【输出形式】

输出分3部分，第1部分输出二维数组m的值，每个元素占8列，然后输出一个空行，第2部分输出二维数组s的值，也是每个元素占8列，再输出一个空行，第3部分输出加括号的方式

【样例输入】

5

30 35 15 5 10 20
【样例输出】
       0   15750    7875    9375   11875
       0       0    2625    4375    7125
       0       0       0     750    2500
       0       0       0       0    1000
       0       0       0       0       0
 
       0       1       1       3       3
       0       0       2       3       3
       0       0       0       3       3
       0       0       0       0       4
       0       0       0       0       0
 
((A1(A2A3))(A4A5))
【提示】

文章来源地址https://www.toymoban.com/news/detail-846333.html

输出加括号的格式需要用一个递归函数

void print(Matrix<int>&S,int i,int j) //Matrix是一个事先定义好的矩阵类

{ int t;

       if(i==j)

       { cout<<"A"<<i;

       return;

       }

       cout<<"(";



S.getData(i,j,t); // 这行代码其实是实现 t=s[i][j]

print(S,i,t);

print(S,t+1,j);

cout<<")";

}
#include "iostream"
#include "iomanip"
using namespace std;
const int N = 1e3;
int m[N][N],s[N][N], p[N];
int n;
void M(){
	for(int r = 2; r <= n; r ++){
		for(int i = 1; i <= n - r + 1; i ++){
			int j = i + r - 1;
			m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j ];
			s[i][j]	= i;
			for(int k = i + 1; k < j; k ++){
				if(m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j] < m[i][j])
				{
					m[i][j] = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
					s[i][j] = k;
				} 
				 
			}
			
		}
	}
}
void print(int i,int j)     //Matrix是一个事先定义好的矩阵类

{   int t;
    if(i == j)
     {  cout<<"A"<<i;
        return;
     }
    cout<<"(";
    t = s[i][j];       // 这行代码其实是实现 t=s[i][j] 
    print(i, t);
    print(t+1, j);
    cout<<")";       

}
int main(){
	cin >> n;
	for(int i = 0; i < n + 1; i ++){
		cin>>p[i];
	}
	M();
	 for(int i = 1; i <= n; i++){
    	for(int j = 1; j <= n; j ++){
    		cout<< setw(8) <<m[i][j];
		}
		cout<<endl;
	}
	cout<<endl;
	for(int i = 1; i <= n; i++){
    	for(int j = 1; j <= n; j ++){
    		cout<< setw(8) <<s[i][j];
		}
		cout<<endl;
	}
	cout<<endl;
	print(1, n);
	return 0;
}

【问题描述】

输入两个序列X和Y，假设序列中都是大写英文字母，且中间没有空格，求出X和Y的最长公共子序列

【输入形式】

输入分2行，分别输入2个序列

【输出形式】

输出分3部分，第1部分输出二维数组C的值，每个元素占3列，然后输出一个空行，第2部分输出二维数组B的值，也是每个元素占3列，再输出一个空行，第3部分输出最长公共子序列，每个字母后加1个空格

把数组B中的方向字符改成用整数表示，0表示 ‘ã’，1表示‘á’，2表示‘ß’

【样例输入】
ABCBDAB
BDCABA
【样例输出】

0 0 0 1 1 1

1 1 1 1 2 2

1 1 2 2 2 2

1 1 2 2 3 3

1 2 2 2 3 3

1 2 2 3 3 4

1 2 2 3 4 4

1 1 1 0 2 0

0 2 2 1 0 2

1 1 0 2 1 1

0 1 1 1 0 2

1 0 1 1 1 1

1 1 1 0 1 0

0 1 1 1 0 1

B C B A

#include "iostream"
#include "iomanip"
#include "vector"
using namespace std;
int B[100][100], C[100][100]; 
vector<char> v;
int main(){
	string a, b;
	cin>>a >>b ;
	for(int i = 0 ; i <= a.length(); i ++){
		for(int j = 0; j <= b.length(); j ++){
			  if(a[i] == b[j]){
				 C[i + 1][j + 1] = C[i][j] + 1;
				 B[i][j] = 0;
			  }
			  else if(C[i + 1][j] <= C[i][j + 1]){
				   C[i + 1][j + 1] = C[i][j + 1];
				   B[i][j] = 1;
			  }
			  else {
				   C[i + 1][j + 1] = C[i + 1][j];
				   B[i][j] = 2;
			  }
		}
	}
	int i = a.length()  - 1, j = b.length() - 1;
	while(i >= 0 && j >= 0){
		if(B[i][j] == 0) v.push_back(a[i]), i --, j --;
		else if(B[i][j] == 1) i --;
		else j --; 
	}
	for(int i = 1; i <= a.length(); i ++){
		for(int j = 1; j <= b.length(); j ++){
			cout<<setw(3)<<C[i][j];
		}
		cout<<endl;
	}
	cout<<endl;
	for(int i = 0; i < a.length(); i ++){
		for(int j = 0; j < b.length(); j ++){
			cout<<setw(3)<<B[i][j];
		}
		cout<<endl;
	}
	cout<<endl;
	while(v.size()){
		cout<<v.back()<<" ";
		v.pop_back();
	}
	return 0;
}

到了这里，关于动态规划的几个经典问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！