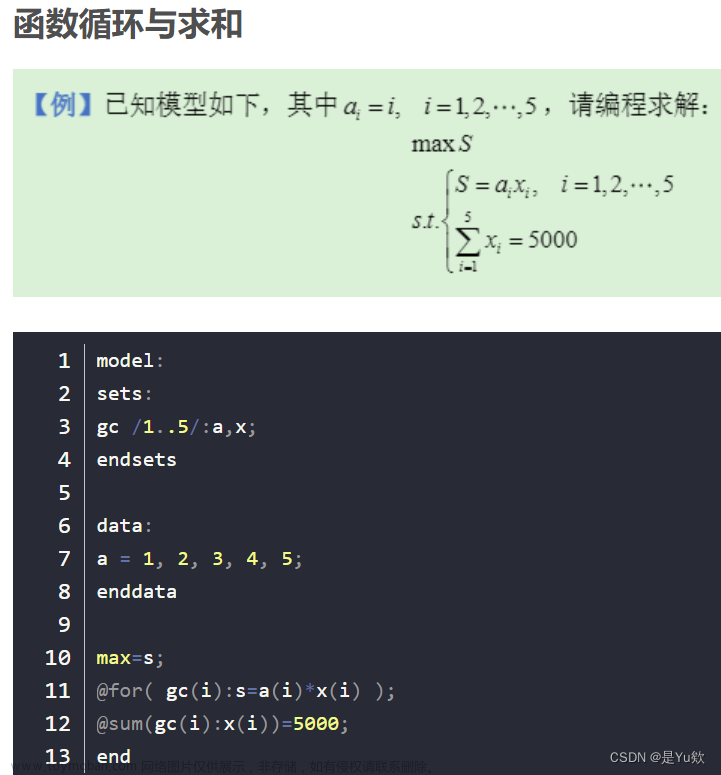
题目：
原料钢管：每根19米
客户需求：4米50根，6米20根，8米15根
问题1：如何切割原料钢管剩余总余量最小？
方法1：直接摆数学公式。
model:
min = 3*x1 + x2 + 3*x3 + 3*x4 + x5 + x6 + 3*x7;
4*x1 + 3*x2 + 2*x3 + x4 + x5 > 50;
x2+2*x4+x5+3*x6 > 20;
x3+x5+2*x7 > 15;
@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);@gin(x6);@gin(x7);
end 方法2：集合和循环方式
model:
sets:
pat/1..7/:x,f;
pipe/1..3/:b;
link(pipe,pat):A;
endsets
data:
f = 3,1,3,3,1,1,3;
b = 50,20,15;
A = 4,3,2,1,1,0,0
0,1,0,2,1,3,0
0,0,1,0,1,1,2;
enddata
min = @sum(pat(i):(f(i)*x(i)));
@for(pipe(i):(@sum(pat(j):A(i,j)*x(j)))> b(i));
@for(pat(i):@gin(x(i)));
end结果图：
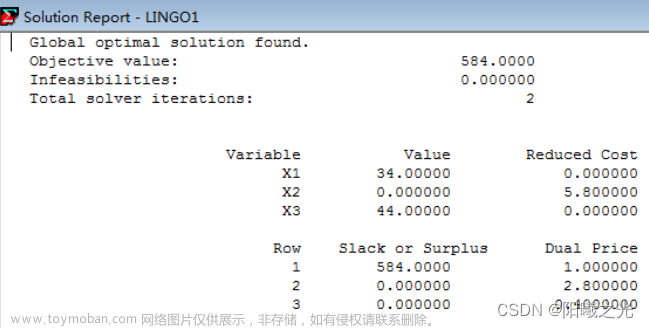
问题2：客户需求增加5米10根，如何保证用到钢材根数最少？
model:
sets:
!四种钢管长度i;
pipe/1..4/:b,c;
!三种模式j;
pat/1..3/:x;
!每根钢管生产4,5,6,8钢管数量;
link(pipe,pat):r;
endsets
data:
b = 50,10,20,15;
c = 4,5,6,8;
enddata
!求钢管数最小;
min = @sum(pat(i):x(i));
!客户需求;
@for(pipe(i):(@sum(pat(j):r(i,j)*x(j)))>b(i));
!余料不超过3m;
@for(pat(j):(@sum(pipe(i):r(i,j)*c(i)))<19);
@for(pat(j):(@sum(pipe(i):r(i,j)*c(i)))>16);
!取整;
@for(pat(i):@gin(x(i)));
@for(pipe(j):@for(pipe(i):@gin(r(i,j))));结果图：
总根数最少为28，x的取值及其切割模式。文章来源：https://www.toymoban.com/news/detail-846384.html
文章来源地址https://www.toymoban.com/news/detail-846384.html
到了这里，关于数学建模 --- Lingo 钢管下料问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
