《数据结构、算法与应用C++语言描述》-列车车厢重排问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了《数据结构、算法与应用C++语言描述》-列车车厢重排问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

完整可编译运行代码见：Github::Data-Structures-Algorithms-and-Applications/_10Train_carriages_rearrangement/

列车车厢重排问题

一列货运列车有 n 节车厢，每节车厢要停靠在不同的车站。假设 n个车站从 1 到n 编号，而且货运列车按照从n到1的顺序经过车站。车厢的编号与它们要停靠的车站编号相同。为了便于从列车上卸掉相应的车厢，必须按照从前至后、从1到 n 的顺序把车厢重新排列。这样排列之后，在每个车站只需卸掉最后一节车厢即可。车厢重排工作在一个转轨站（shunting yard）上进行，转轨站上有一个入轨道（input track）、一个出轨道（output track）和k个缓冲轨道（holding track）。缓冲轨道位于入轨道和出轨道之间。图 8-6a 显示了一个转轨站，其中有 3 个缓冲轨道 H1、H2 和 H3，即 k=3。开始时，挂有 n 节车厢的货车开始在入轨道，而最后在出轨道上的顺序是从右到左，从1 至n。在图 8-6a 中，n=9，车厢从后至前的初始顺序为5，8，1，7，4，2，9，6，3。图8-6b是按要求的顺序重新排列的结果。
c++实现火车车厢重排问题,数据结构、算法与应用 C++语言描述学习笔记,数据结构,算法,c++

使用栈解决

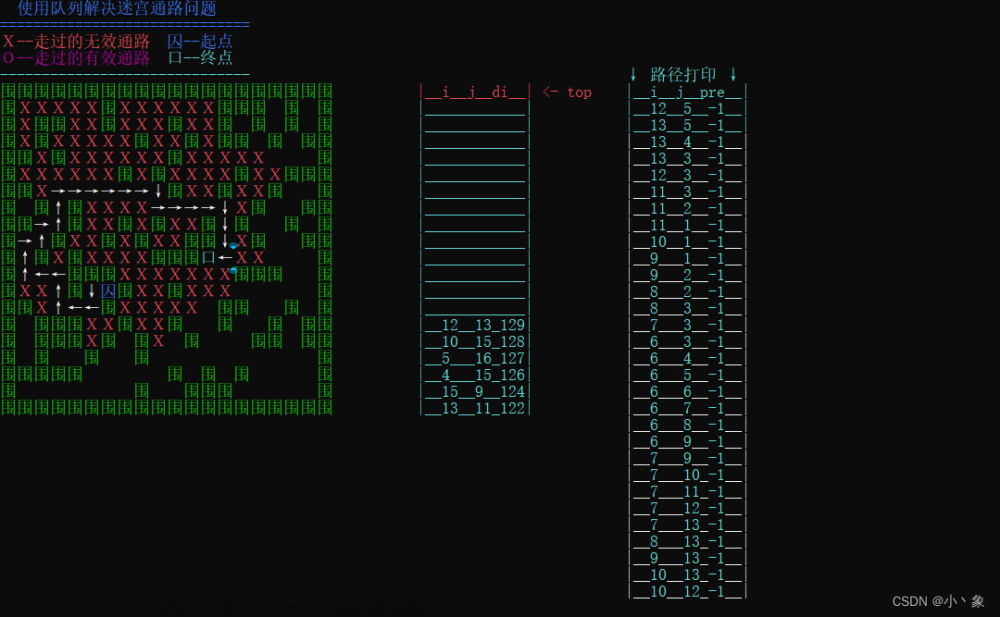
思路

为了重排车厢，我们从前至后检查入轨道上的车厢。如果正在检查的车厢是满足排列要求的下一节车厢，就直接把它移到出轨道上。如果不是，就把它移到一个缓冲轨道上，直到它满足排列要求时才将它移到出轨道上。缓冲轨道是按照 LIFO的方式管理的，车厢的进出都在缓冲轨道的顶部进行。在重排车厢过程中，仅允许以下移动：

车厢可以从入轨道的前端（即右端）移动到一个缓冲轨道的顶部或出轨道的后端（即左端）。
车厢可以从一个缓冲轨道的顶部移到出轨道的后端。
使用单调栈，栈顶到栈底的元素从小到大。

代码

#include <iostream>
#include <stack>
#include <vector>
using namespace std;
/*列车车厢重排全局变量*/
stack<int>* trackStack;//缓冲轨道数组
vector<int> outputTrackStack;//输出数组
int numberOfCarsStack;//需要重排的列车数目
int numberOfTracksStack;//缓冲轨道数目
int smallestCarStack;//在缓冲轨道中编号最小的车厢
int itsTrackStack;//停靠着最小编号车厢的缓冲轨道

/*列车车厢重排问题*/
/*将编号最小的车厢从缓冲轨道移到出轨道*/
void outputFromHoldingTrackStack()
{
    //从栈itsTrack中删除编号最小的车厢
    outputTrackStack.push_back(trackStack[itsTrackStack].top());
    trackStack[itsTrackStack].pop();
    cout << "Move car " << smallestCarStack << " from holding track " << itsTrackStack << " to output track" << endl;
    //检查所有的栈顶，寻找编号最小的车厢和它所属的栈itsTrack
    smallestCarStack = numberOfCarsStack + 2;
    for (int i = 1; i <= numberOfTracksStack; i++)
    {
        if (!trackStack[i].empty() && (trackStack[i].top() < smallestCarStack))
        {
            smallestCarStack = trackStack[i].top();
            itsTrackStack = i;
        }
    }
}
/*将车厢c移到一个缓冲轨道。返回false,当且仅当没有可用的缓冲轨道*/
bool putInHoldingTrackStack(int c)
{
    //为车厢c寻找最适合的缓冲轨道
    //初始化
    int bestTrack = 0;//目前没有适合的缓冲轨道
    int bestTop = numberOfCarsStack + 1;//取bestTrack中最顶部的车厢，便于比较
    //扫描缓冲轨道
    for (int i = 1; i <= numberOfTracksStack; i++)
    {
        //缓冲轨道i不为空
        // 是一个单调栈，栈底到栈顶的数据是从小到大
        if (!trackStack[i].empty())
        {
            if (c < trackStack[i].top() && trackStack[i].top() < bestTop)
            {//缓冲轨道i的栈顶具有编号更小的车厢
                bestTop = trackStack[i].top();
                bestTrack = i;
            }
        }
        else if (bestTrack == 0) bestTrack = i;
    }
    if (bestTrack == 0) return false;//没有可用的缓冲轨道
    //把车厢c移动到轨道bestTrack
    trackStack[bestTrack].push(c);
    cout << "Move car " << c << " from input track to holding track " << bestTrack << endl;
    //如果需要，更新smallestCar和itsTrack
    if (c < smallestCarStack)
    {
        smallestCarStack = c;
        itsTrackStack = bestTrack;
    }
    return true;
}
/*从初始顺序开始重排车厢；如果重排成功，返回true,否则返回false*/
bool railRoadStack(int inputOrder[], int theNumberOfCars, int theNumberOfTracks)
{
    numberOfCarsStack = theNumberOfCars;
    numberOfTracksStack = theNumberOfTracks;
    /*创建用于缓冲轨道的栈*/
    trackStack = new stack<int>[numberOfTracksStack + 1];
    smallestCarStack = numberOfCarsStack + 1;//缓冲轨道中无车厢

    int nextCarToOutput = 1;//当前需要被输出轨道的车厢编号
    //重排车厢
    for (int i = 0; i < numberOfCarsStack; i++)
    {
        if (inputOrder[i] == nextCarToOutput)
        {
            /*将车厢inputOrder[i]直接移到出轨道*/
            cout << "Move car " << inputOrder[i] << " from input track to output track" << endl;
            outputTrackStack.push_back(inputOrder[i]);
            nextCarToOutput++;
            /*从缓冲轨道移到出轨道*/
            while (smallestCarStack == nextCarToOutput)
            {
                outputFromHoldingTrackStack();
                nextCarToOutput++;
            }
        }
        else
        {
            if(!putInHoldingTrackStack(inputOrder[i]))
                return false;
        }
    }
    return true;
}

int main()
{
    // 列车车厢重排问题
    cout << "railRoadStack()*****************" << endl;
    int inputOrder[9] = { 5, 8, 1, 7, 4, 2, 9, 6, 3 };
    railRoadStack(inputOrder, 9, 3);
    for(int& data : outputTrackStack)
        cout << data << " ";
    cout << endl;
    return 0;
}

运行结果

C:\Users\15495\Documents\Jasmine\Work\coding\cmake-build-debug\coding.exe
railRoadStack()*****************
Move car 5 from input track to holding track 1
Move car 8 from input track to holding track 2
Move car 1 from input track to output track
Move car 7 from input track to holding track 2
Move car 4 from input track to holding track 1
Move car 2 from input track to output track
Move car 9 from input track to holding track 3
Move car 6 from input track to holding track 2
Move car 3 from input track to output track
Move car 4 from holding track 1 to output track
Move car 5 from holding track 1 to output track
Move car 6 from holding track 2 to output track
Move car 7 from holding track 2 to output track
Move car 8 from holding track 2 to output track
Move car 9 from holding track 3 to output track
1 2 3 4 5 6 7 8 9

Process finished with exit code 0

使用队列解决

思路

为了重排车厢，我们从前至后检查入轨道上的车厢。如果正在检查的车厢是满足排列要求的下一节车厢，就直接把它移到出轨道上。如果不是，就把它移到一个缓冲轨道上，直到它满足排列要求时才将它移到出轨道上。缓冲轨道是按照 LILO的方式管理的，车厢的进出都在缓冲轨道的队头进行。在重排车厢过程中，仅允许以下移动：

车厢可以从入轨道的前端（即右端）移动到一个缓冲轨道的队尾或出轨道的后端（即左端）。
车厢可以从一个缓冲轨道的队头移到出轨道的后端。
使用单调队列，队头到队尾的元素从小到大。

代码

#include <iostream>
#include <queue>
using namespace std;
/*列车车厢重排全局变量*/
queue<int>* trackQueue;//缓冲轨道数组
queue<int> outputTrackQueue;//输出数组
int numberOfCarsQueue;//需要重排的列车数目
int numberOfTracksQueue;//缓冲轨道数目
int smallestCarQueue;//在缓冲轨道中编号最小的车厢
int itsTrackQueue;//停靠着最小编号车厢的缓冲轨道

/*列车车厢重排问题*/
/*将编号最小的车厢从缓冲轨道移到出轨道*/
void outputFromHoldingTrackQueue()
{
    //从队列itsTrack中删除编号最小的车厢
    outputTrackQueue.push(smallestCarQueue);
    trackQueue[itsTrackQueue].pop();
    cout << "Move car " << smallestCarQueue << " from holding track " << itsTrackQueue << " to output track" << endl;
    //检查所有的队头，寻找编号最小的车厢和它所属的队itsTrackQueue
    smallestCarQueue = numberOfCarsQueue + 2;
    for (int i = 1; i <= numberOfTracksQueue; i++)
    {
        if (!trackQueue[i].empty() && (trackQueue[i].front() < smallestCarQueue))
        {
            smallestCarQueue = trackQueue[i].front();
            itsTrackQueue = i;
        }
    }
}
/*将车厢c移到一个缓冲轨道。返回false,当且仅当没有可用的缓冲轨道*/
/*此处使用了单调队列：从队头元素到队尾元素是从小到大的顺序*/
bool putInHoldingTrackQueue(int c)
{
    //为车厢c寻找最适合的缓冲轨道
    //初始化
    int bestTrack = 0;//目前没有适合的缓冲轨道
    int bestTop = 0;//取bestTrack为0，便于比较
    //扫描缓冲轨道
    for (int i = 1; i <= numberOfTracksQueue; i++)
    {
        //缓冲轨道i不为空
        if (!trackQueue[i].empty())
        {
            if (c > trackQueue[i].back() && trackQueue[i].back() > bestTop)
            {//缓冲轨道i的队尾具有编号更大的车厢
                bestTop = trackQueue[i].back();
                bestTrack = i;
            }
        }
        else//缓冲轨道i为空
            if (bestTrack == 0) bestTrack = i;
    }
    if (bestTrack == 0) return false;//没有可用的缓冲轨道
    //把车厢c移动到轨道bestTrack
    trackQueue[bestTrack].push(c);
    cout << "Move car " << c << " from input track to holding track " << bestTrack << endl;
    //如果需要，更新smallestCar和itsTrack
    if (c < smallestCarQueue)
    {
        smallestCarQueue = c;
        itsTrackQueue = bestTrack;
    }
    return true;
}
/*从初始顺序开始重排车厢；如果重排成功，返回true,否则返回false*/
bool railRoadQueue(int inputOrder[], int theNumberOfCars, int theNumberOfTracks)
{
    numberOfCarsQueue = theNumberOfCars;
    numberOfTracksQueue = theNumberOfTracks;
    /*创建用于缓冲轨道的队列*/
    trackQueue = new queue<int>[numberOfTracksQueue + 1];
    smallestCarQueue = numberOfCarsQueue + 1;//缓冲轨道中无车厢

    int nextCarToOutput = 1;//当前需要被输出轨道的车厢编号
    //重排车厢
    for (int i = 0; i < numberOfCarsQueue; i++)
    {
        if (inputOrder[i] == nextCarToOutput)
        {
            /*将车厢inputOrder[i]直接移到出轨道*/
            cout << "Move car " << inputOrder[i] << " from input track to output track" << endl;
            outputTrackQueue.push(inputOrder[i]);
            nextCarToOutput++;
            /*从缓冲轨道移到出轨道*/
            while (smallestCarQueue == nextCarToOutput)
            {
                outputFromHoldingTrackQueue();
                nextCarToOutput++;
            }
        }
        else
        {
            if (!putInHoldingTrackQueue(inputOrder[i]))
                return false;
        }
    }
    return true;
}


int main()
{
    //列车车厢重排问题
    cout << "railRoadQueue()*****************" << endl;
    int inputOrder[9] = { 5, 8, 1, 7, 4, 2, 9, 6, 3 };
    if(railRoadQueue(inputOrder, 9, 3)){
        for(int i = 0; i < outputTrackQueue.size(); i++){
            cout << outputTrackQueue.front() << " ";
            outputTrackQueue.pop();
        }
        cout << endl;
    }

    return 0;
}

运行结果

C:\Users\15495\Documents\Jasmine\Work\coding\cmake-build-debug\coding.exe
railRoadQueue()*****************
Move car 5 from input track to holding track 1
Move car 8 from input track to holding track 1
Move car 1 from input track to output track
Move car 7 from input track to holding track 2
Move car 4 from input track to holding track 3
Move car 2 from input track to output track
Move car 9 from input track to holding track 1
Move car 6 from input track to holding track 3
Move car 3 from input track to output track
Move car 4 from holding track 3 to output track
Move car 5 from holding track 1 to output track
Move car 6 from holding track 3 to output track
Move car 7 from holding track 2 to output track
Move car 8 from holding track 1 to output track
Move car 9 from holding track 1 to output track
1 2 3 4 5

Process finished with exit code 0

既不使用栈也不使用队列解决

思路

使用数组模拟单调栈或单调队列。文章来源地址https://www.toymoban.com/news/detail-846858.html

代码

#include <iostream>
using namespace std;
/*不使用队列的列车车厢重排全局变量*/
/*存储车厢所在的轨道和轨道队尾的值*/
int* whichTrack;  // track that has the car,存储了某车子在哪个轨道
int* lastCar;     // last car in track
int numberOfCars;
int numberOfTracks;

/*不使用队列的列车车厢重排问题*/
void outputFromHoldingTrackNoQueues(int c)
{// Move car c from its holding track to the output track.
    cout << "Move car " << c << " from holding track "
         << whichTrack[c] << " to output track" << endl;

    // if c was the last car in its track, the track is now empty
    if (c == lastCar[whichTrack[c]])
        lastCar[whichTrack[c]] = 0;
}
bool putInHoldingTrackNoQueues(int c)
{// Put car c into a holding track.
    // Return false iff there is no feasible holding track for this car.

    // find best holding track for car c
    // initialize
    int bestTrack = 0,  // best track so far
    bestLast = 0;  // last car in bestTrack

    // scan tracks
    for (int i = 1; i <= numberOfTracks; i++)
        if (lastCar[i] != 0)
        {// track i not empty
            if (c > lastCar[i] && lastCar[i] > bestLast)
            {
                // track i has bigger car at its rear
                bestLast = lastCar[i];
                bestTrack = i;
            }
        }
        else // track i empty
            if (bestTrack == 0)
                bestTrack = i;

    if (bestTrack == 0)
        return false; // no feasible track

    // add c to bestTrack
    whichTrack[c] = bestTrack;
    lastCar[bestTrack] = c;
    cout << "Move car " << c << " from input track "
         << "to holding track " << bestTrack << endl;

    return true;
}
bool railroadNoQueues(int* inputOrder, int theNumberOfCars, int theNumberOfTracks)
{// Rearrange railroad cars beginning with the initial order.
    // inputOrder[1:theNumberOfCars]
    // Return true if successful, false if impossible.

    numberOfCars = theNumberOfCars;
    // keep last track open for output
    numberOfTracks = theNumberOfTracks - 1;

    // create the arrays lastCar and whichTrack
    lastCar = new int[numberOfTracks + 1];
    fill(lastCar + 1, lastCar + numberOfTracks + 1, 0);
    whichTrack = new int[numberOfCars + 1];
    fill(whichTrack + 1, whichTrack + numberOfCars + 1, 0);

    int nextCarToOutput = 1;

    // rearrange cars
    for (int i = 1; i <= numberOfCars; i++)
        if (inputOrder[i] == nextCarToOutput)
        {// send car inputOrder[i] straight out
            cout << "Move car " << inputOrder[i] << " from input "
                 << "track to output track" << endl;
            nextCarToOutput++;

            // output from holding tracks
            while (nextCarToOutput <= numberOfCars &&
                   whichTrack[nextCarToOutput] != 0)
            {
                outputFromHoldingTrackNoQueues(nextCarToOutput);
                nextCarToOutput++;
            }
        }
        else
            // put car inputOrder[i] in a holding track
            if (!putInHoldingTrackNoQueues(inputOrder[i]))
                return false;
    return true;
}


int main()
{
    //列车车厢重排问题
    cout << "railroadNoQueues()**************" << endl;
    int p[] = {0, 3, 6, 9, 2, 4, 7, 1, 8, 5};
    cout << "Input permutation is 369247185" << endl;
    railroadNoQueues(p, 9, 3);

    return 0;
}

运行结果

C:\Users\15495\Documents\Jasmine\Work\coding\cmake-build-debug\coding.exe
railroadNoQueues()**************
Input permutation is 369247185
Move car 3 from input track to holding track 1
Move car 6 from input track to holding track 1
Move car 9 from input track to holding track 1
Move car 2 from input track to holding track 2
Move car 4 from input track to holding track 2
Move car 7 from input track to holding track 2
Move car 1 from input track to output track
Move car 2 from holding track 2 to output track
Move car 3 from holding track 1 to output track
Move car 4 from holding track 2 to output track
Move car 8 from input track to holding track 2
Move car 5 from input track to output track
Move car 6 from holding track 1 to output track
Move car 7 from holding track 2 to output track
Move car 8 from holding track 2 to output track
Move car 9 from holding track 1 to output track

Process finished with exit code 0

到了这里，关于《数据结构、算法与应用C++语言描述》-列车车厢重排问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！