完全背包&多重背包问题（动态规划）-Toy模板网

这篇具有很好参考价值的文章主要介绍了完全背包&多重背包问题（动态规划）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

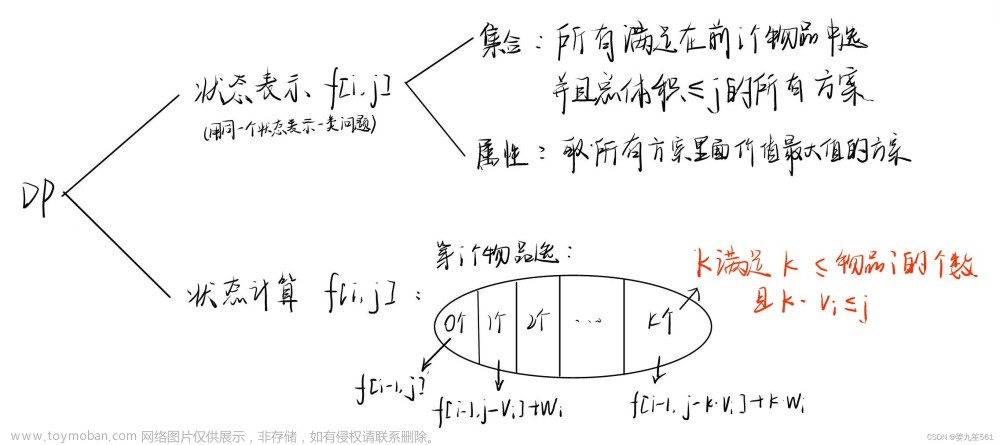
完全背包问题：

每个物品使用次数没有限制，与0-1背包的不同之处在于遍历背包的顺序是正序。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n, v;
    cin >> n >> v;
    vector<int> weight(n), values(n), dp(v+1, 0); // dp[j]：容量为j的背包的最大价值
    for(int i=0; i<n; i++){
        cin >> weight[i] >> values[i];
    }
    for(int i=0; i<n; i++){
        for(int j=weight[i]; j<=v; j++){ // j的取值比较关键
            dp[j] = max(dp[j], dp[j-weight[i]]+values[i]);
        }
    }
    cout << dp[v];
    return 0;
}

多重背包问题：

与完全背包的区别在于，每一种物品是有个数限制的，不能无限选择。这篇博客讲解的非常详细，可以参考学习：

多重背包问题---超详细讲解+优化（不懂你揍我）-CSDN博客文章浏览阅读2.1w次，点赞83次，收藏259次。多重背包我们其实可以看成为01背包和完全背包的组合。但是怎么组合的呢？也可以就把多重背包问题转换成01背包问题，我们一起来看看解题思路。1.状态表示DP问题我们先来看状态表示二维数组的表示，F[i][j]代表前 i 个物品中，背包容量为 j 时所能拿到的最大价值。然后我们就看如何把多重背包转换成01背包与完全背包。2.转换（1）转换为01背包我们知道，01背包问题指的是各个物品只有一件，但在多重背包问题中，我们每种物品有 Si 件。我们可以考虑将多个同种物品合成一件物品。.._多重背包https://blog.csdn.net/windfriendc/article/details/123892024

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n, v;
    cin >> n >> v;
    vector<int> weight(n), values(n), nums(n), dp(v+1, 0);
    for(int i=0; i<n; i++){
        cin >> weight[i] >> values[i] >> nums[i];
    }
    for(int i=0; i<n; i++){ // 先遍历物品
        if(nums[i]*weight[i] >= v){ // 如果nums[i]*weight[i] >= v，则可以转换为完全背包问题
            for(int j=weight[i]; j<=v; j++){ // 完全背包要正序遍历
                dp[j] = max(dp[j], dp[j-weight[i]]+values[i]);
            }
        }else{ // 否则转换为0-1背包问题
            for(int j=v; j>=weight[i]; j--){ // 0-1背包要倒序遍历
                for(int k=nums[i]; k>=0; k--){ // 每件物品有k的数量限制
                    if(j >= k*weight[i])
                        dp[j] = max(dp[j], dp[j-k*weight[i]]+k*values[i]);
                }
            }
        }
    }
    cout << dp[v];
    return 0;
}

多重背包问题的二进制优化：

假设我们想要拿1024件物品，按照转化成0-1背包的方法做，我们需要从拿1件枚举到拿1024件。而二进制优化则是利用倍增思想，把拿多少件物品分为拿1、2、4、8、16、...、256、512、...、件，枚举的时候10次就到1024件了。基于上述思想，无论是多少件，总能用一些数的组合来表示，比如15（二进制形式：1111）就可以用8 + 4 + 2 + 1来表示，只需要枚举4次。这就是二进制优化的思想。

解题思路：将1、2、4...的物品分别保存下来它们的重量和价值，然后转化为0-1背包问题。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N, V;
    cin >> N >> V;
    vector<int> s(N), v(N), w(N), dp(V+1, 0);
    vector<int> biV, biW; // 合成的新物品体积和价值
    
    for(int i=0; i<N; i++){
        cin >> v[i] >> w[i] >> s[i];
        for(int k=1; k<=s[i]; s[i]-=k, k*=2){ // 用k取遍物品i所有个数，这里的 s[i]-=k, k*=2 顺序不能变，否则会出错
            biV.push_back(k*v[i]);
            biW.push_back(k*w[i]);
        }
        if(s[i] > 0){
            biV.push_back(s[i]*v[i]);
            biW.push_back(s[i]*w[i]);
        }
    }
    
    for(int i=0; i<biV.size(); i++){ // 转换成0-1背包
        for(int j=V; j>=biV[i]; j--){
            dp[j] = max(dp[j], dp[j-biV[i]]+biW[i]);
        }
    }
    cout << dp[V];
    return 0;
}

以上代码均为测试用的样例代码，实际问题需要根据题目要求进行修改。文章来源地址https://www.toymoban.com/news/detail-846919.html

到了这里，关于完全背包&多重背包问题（动态规划）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！