目录
第一章 行列式
1.1 行列式的几何意义
1.2 什么是线性相关,线性无关
1.3 行列式几何意义
1.4 行列式求和
1.5 行列式其他性质
1.6 余子式
1.7 对角线行列式
1.8 分块行列式
1.9 范德蒙德行列式
1.10 爪形行列式的计算
第二章 矩阵
2.1 初识矩阵
2.1.1 矩阵的概念
1.1.2 矩阵的运算规律
2.2 矩阵的转置
2.3 伴随矩阵
2.3.1 伴随矩阵的定义
2.3.2 伴随矩阵的性质
2.4 矩阵的逆
2.4.1 逆矩阵的定义
2.4.2 逆矩阵的性质
2.4.3 矩阵逆的公式
2.5 转置、伴随、逆
2.6 矩阵的初等变换
2.6.1 矩阵等价的条件
2.6.2 初等矩阵的性质
2.6.3 初等矩阵的逆、转置和伴随
2.6.4 可逆矩阵方程
第三章 矩阵的秩
3.1 引出矩阵方程的秩:
3.2 矩阵秩的定义
3.3 矩阵秩的性质
3.4 矩阵秩的结论
3.4.1 秩的结论1
3.4.2 秩的结论2
3.4.3 秩的结论3
3.4.4 秩的结论4
3.4.5 秩的结论5
3.4.6 秩的结论6
3.5 矩阵秩的例题
第四章 向量组
4.1 向量的定义
4.2 线性表示
4.3 向量组等价
4.3.1 向量组等价定义:
4.3.2 矩阵等价和向量组等价
4.3.3 向量等价的推论
4.4 线性相关性
4.4.1 线性相关性定义
4.4.2 线性相关与秩的关系
4.4.3 线性相关的例题
4.4.4 关于线性相关的定义
4.5. 极大无关组
4.6. 向量组的秩
第五章 线性方程组
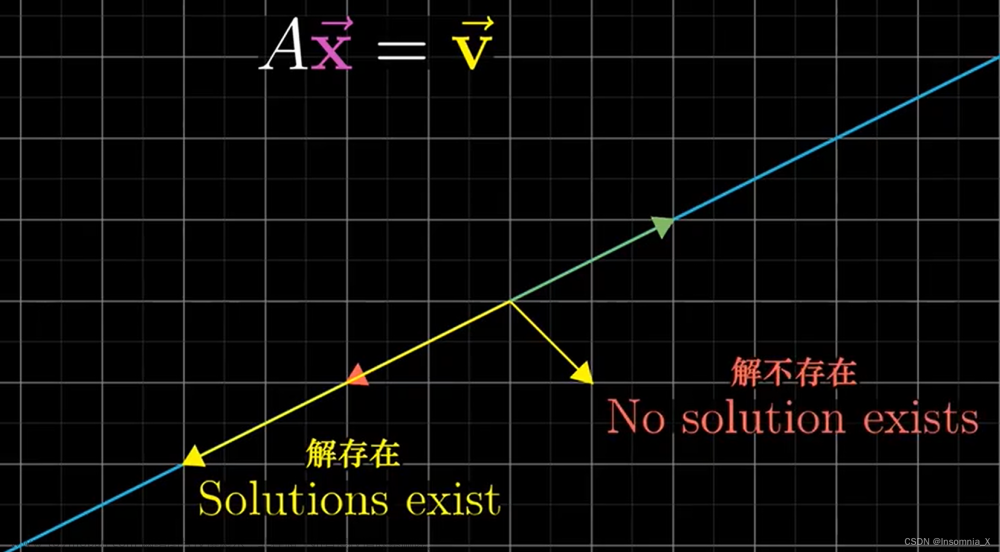
5.1 方程的解的判定
5.1.1 齐次方程的解的判定
5.1.2 非齐次方程的解的判定
5.2 方程组求解的例题
5.3 基础解系
5.4 解的结构
5.5 求通解的步骤
第六章 特征值和特征向量
6.1 特征值和特征向量的定义
6.2 特征值的性质
6.3 特征向量的性质
第七章 相识对角化
7.1 相似矩阵的定义
7.2 相似矩阵的性质
7.3 相似对角化
7.4 相似对角化的性质
7.5 秩为一的矩阵
7.6 合同最小化
7.6.1 实对称矩阵的性质
7.6.2 例题
第八章 二次型
8.1. 合同对角化与正交变换法的步骤:
第一章 行列式
1.1 行列式的几何意义
答:2阶行列式是一个平行四边形的面积,3阶行列式是一个3个向量组成的平行六面体的体积,n阶行列式是n个向量为邻边的n维图形的体积。
1.2 什么是线性相关,线性无关

1.3 行列式几何意义
- 2阶行列式中的其中一行为0,则组不成面积,3阶行列式中的其中一行为0,则组不成体积,2阶行列式中的其中两行(列)相等,则组不成面积,3阶行列式中的其中两行(列)相等,则组不成体积。
- 若行列式中某行(列)元素有公因子K,则K可提到行列式外面,即几何理解:例如:2阶行列式中的其中一行乘以K,则面积就是K倍。
1.4 行列式求和
行列式中某行(列)元素均是两个元素之和,则可拆成两个行列式之和,即

1.5 行列式其他性质
- 行列式中两行(列)互换,行列式的值反号.
- 行列式中某行(列)的K倍加到另一行(列),行列式的值不变
例题:求一下下面的:

技巧:
1、取完第一个数字,就要去掉所在行和所在列
2、前面的额正负号可以用交换改变逆序数的正负号的方法。

2阶行列式和3阶行列式的计算。(用到的是画图发)

1.6 余子式
什么是余子式和代数余子式,并一般用什么表示?

行列式按某一行(列)展开的展开公式

1.7 对角线行列式

1.8 分块行列式
A为m 阶矩阵,B为 阶矩阵则

1.9 范德蒙德行列式

1.10 爪形行列式的计算
例如:


第二章 矩阵
2.1 初识矩阵
2.1.1 矩阵的概念
矩阵就是一个数表,就和1,2,3的性质一样。
行列式是一种运算符号,就和加减乘除一样。
注意:
1.1.2 矩阵的运算规律
例1:


例2:


例3


例4


2.2 矩阵的转置
矩阵的性质1:


矩阵的性质2:


来个例题:


2.3 伴随矩阵
2.3.1 伴随矩阵的定义




2.3.2 伴随矩阵的性质


证明下列:


2.4 矩阵的逆
2.4.1 逆矩阵的定义
AB = BA = E


2.4.2 逆矩阵的性质





2.4.3 矩阵逆的公式






2.5 转置、伴随、逆


2.6 矩阵的初等变换
2.6.1 矩阵等价的条件
- 同型矩阵
- 秩相同(初等行和初等列变换以后)
2.6.2 初等矩阵的性质
- 对n阶矩阵A进行初等行变换,相当于矩阵A左乘相应的初等矩阵,
- 对n阶矩阵A进行初等列变换,相当于矩阵A右乘相应的初等矩阵。

来个例题:


2.6.3 初等矩阵的逆、转置和伴随





来个例题1:


例题2


2.6.4 可逆矩阵方程

来例题:


在来个例题:


第三章 矩阵的秩
3.1 引出矩阵方程的秩:
如下方程用矩阵表示的:
- 系数矩阵的列表示表示什么?
- 矩阵的行表示什么?
- 那么矩阵的有效个数是什么呢?

- 系数矩阵的列表示表示未知数的个数。
- 矩阵的行表示总方程个数。
- 那么矩阵的有效个数是什么呢?排除混子就是,也就是矩阵的秩。
3.2 矩阵秩的定义

3.3 矩阵秩的性质


3.4 矩阵秩的结论
3.4.1 秩的结论1


3.4.2 秩的结论2


3.4.3 秩的结论3


3.4.4 秩的结论4


3.4.5 秩的结论5



3.4.6 秩的结论6



3.5 矩阵秩的例题



第四章 向量组
4.1 向量的定义

4.2 线性表示


4.3 向量组等价
4.3.1 向量组等价定义:

4.3.2 矩阵等价和向量组等价
- 矩阵等价:同型矩阵,秩相等。
- 向量组等价:可以相互表示即(几何:可以决定同一个空间):R(A,B) = R(A) = R(B)
- 注意:向量组等价是同一个空间,而不是相同的秩,相同的秩,只能说明相同的维度,但不一定在同一个空间。

4.3.3 向量等价的推论


4.4 线性相关性
4.4.1 线性相关性定义
- 线性相关:可以有线性表示就是线性相关,不可以线性表示就是线性无关,即有无混子。
- 齐次方程组有非零解,说明解向量中有混子,这个混子可以被其他向量表示,也线性相关。

4.4.2 线性相关与秩的关系
- 向量的秩小于向量的个数:向量空间的理解:m个向量决定了空间的维度,但是达不到m,说明有混子向量,如果都是骨干向量的话,m个向量就决定了m维度。

4.4.3 线性相关的例题



4.4.4 关于线性相关的定义

4.5. 极大无关组

- 行变不改变列向量组内的线性表示关系
4.6. 向量组的秩

第五章 线性方程组
5.1 方程的解的判定
5.1.1 齐次方程的解的判定




5.1.2 非齐次方程的解的判定




5.2 方程组求解的例题



5.3 基础解系




5.4 解的结构




5.5 求通解的步骤




第六章 特征值和特征向量
6.1 特征值和特征向量的定义
一个矩阵的乘以一个向量 == 一个数乘以一个向量
理解:


例题1:



例题2:



6.2 特征值的性质


6.3 特征向量的性质
- 不同的特征值对应的特征向量是线性无关的。



例题:


例题:


第七章 相识对角化
7.1 相似矩阵的定义




7.2 相似矩阵的性质


7.3 相似对角化

所以:所有拉姆达线性无关的话:




4、相似对角化的性质


4.1 例题1



7.4 相似对角化的性质


例题1



思考的问题:



例题2


7.5 秩为一的矩阵


7.6 合同最小化
7.6.1 实对称矩阵的性质

7.6.2 例题


第八章 二次型
8.1. 合同对角化与正交变换法的步骤:
 文章来源:https://www.toymoban.com/news/detail-847010.html
文章来源:https://www.toymoban.com/news/detail-847010.html
- 二次型矩阵的特点:一定是对称矩阵,对角线是平方项。
- 标准型和规范型
标准型:系数不一定为1,
规范型,系数为1或-1。 - 正交变换为标准型的系数:一定是特征值。
- 判断两个矩阵是否合同:主要看他们的正负惯性指数一样,也就是系数正负是否一样,也就是特征值的正负是否一样。
-
正定矩阵的条件:
- 必须是对称矩阵
- 方程系数都为正,或者二次矩阵的特征值都为正。
-
判别正定矩阵A:
- A是实对称矩阵
- 所有顺序主子式均>0
- 主对角元素都大于0;
- A中最大的数落在主对角线上
-
对称矩阵A为负定的充分必要条件是:
- 奇数阶主子式为负,而偶数阶主子式为正。
本章完。文章来源地址https://www.toymoban.com/news/detail-847010.html
到了这里,关于【考研数学二】线性代数重点笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!