回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测-Toy模板网

这篇具有很好参考价值的文章主要介绍了回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测

预测效果

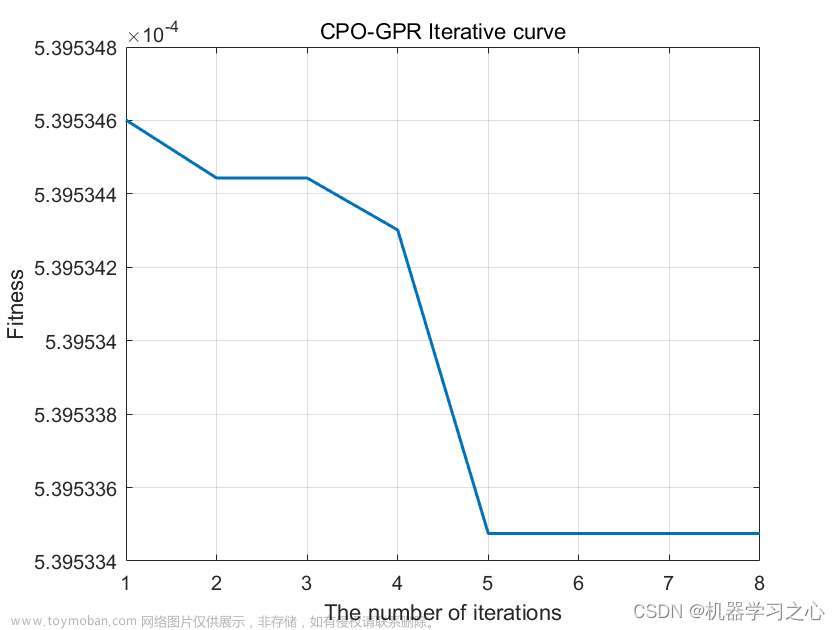
回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测,回归预测,CPO-GPR,冠豪猪算法优化,高斯过程回归,多输入单输出回归预测

基本介绍

Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的数据回归预测（完整源码和数据)
1.Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的输入多个特征，输出单个变量，多输入单输出回归预测；
3.多指标评价，评价指标包括：R2、MAE、MSE、RMSE等，代码质量极高；
4.粒子群算法优化参数为：优化核函数超参数 sigma，标准差，初始噪声标准差；
5.excel数据，方便替换，运行环境2018及以上。

程序设计

完整程序和数据获取方式(资源处下载):Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的数据回归预测

%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行
% restoredefaultpath
%%  导入数据
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
f_ =size(P_train, 1); %输入特征维度
M = size(P_train, 2);
N = size(P_test, 2);
%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  超参数设置
Best_pos = [0.6, 0.7, 30];    % 优化下界

%%  仿真测试
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 数据转置
T_sim1=T_sim1';
T_sim2 =T_sim2';
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);

%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%
%决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%
%均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
%%
%RPD 剩余预测残差
SE1=std(T_sim1-T_train);
RPD1=std(T_train)/SE1;
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
SE=std(T_sim2-T_test);
RPD2=std(T_test)/SE;
%% 平均绝对误差MAE
MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 测试集误差图
figure  
ERROR3=T_test-T_sim2;
plot(T_test-T_sim2,'b-*','LineWidth',1.5)
xlabel('测试集样本编号')
ylabel('预测误差')
title('测试集预测误差')
grid on;
legend('GPR预测输出误差')
%% 打印出评价指标
disp(['-----------------------误差计算--------------------------'])
disp(['评价结果如下所示：'])
disp(['平均绝对误差MAE为：',num2str(MAE2)])
disp(['均方误差MSE为：       ',num2str(mse2)])
disp(['均方根误差RMSEP为：  ',num2str(error2)])
disp(['决定系数R^2为：  ',num2str(R2)])
disp(['剩余预测残差RPD为：  ',num2str(RPD2)])
disp(['平均绝对百分比误差MAPE为：  ',num2str(MAPE2)])

参考资料

[1]https://blog.csdn.net/kjm13182345320/article/details/124443069?spm=1001.2014.3001.5501
[2]https://blog.csdn.net/kjm13182345320/article/details/124443735?spm=1001.2014.3001.5501文章来源地址https://www.toymoban.com/news/detail-847202.html

到了这里，关于回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！