动态规划：矩阵连乘问题，字节跳动今日学习内容-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划：矩阵连乘问题，字节跳动今日学习内容。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

分析：

二.问题分析

由于矩阵乘法满足结合律，所以计算矩阵连乘的连乘积可以与许多不同的计算计算次序，这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说连乘积已完全加括号，那么可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

完全加括号的矩阵连乘积可递归地定义为：

（1）.单个矩阵是完全加括号的；

（2）.矩阵连乘积A是完全加括号的，则A可以表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，及A=（BC）

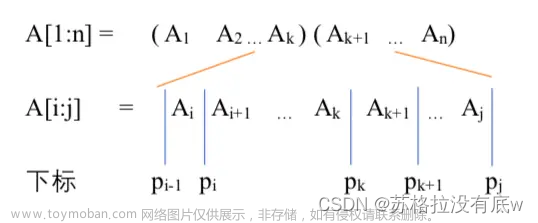
举个例子，矩阵连乘积A1A2A3A4A5，可以有5种不同的完全加括号方式：

(A1(A2(A3A4))),(A1((A2A3)A4)),((A1A2)(A3A4)),((A1(A2A3))A4),(((A1A2)A3)A4)

每一种完全加括号的方式对应一种矩阵连乘积的计算次序，而矩阵连乘积的计算次序与其计算量有密切的关系，即与矩阵的行和列有关。

补充一下数学知识，矩阵A与矩阵B可乘的条件为矩阵A的列数等于矩阵B的行数，例如，若A是一个p_q的矩阵，B是一个q_r的矩阵，则其乘积C=AB是一个p*r的矩阵。

源码如下：

#include

using namespace std;

#define max 255

int a[max],m[max][max];

int Getmin(int i,int j)

{

int min,n;

if(m[i][j]>=0)

return m[i][j];

if(i==j)

return 0;

if(i==j-1)

{

m[i][j]=a[i]*a[i+1]*a[i+2];

return m[i][j];

}

min=Getmin(i,i)+Getmin(i+1,j)+a[i]*a[i+1]*a[j+1];

for(int k=i+1;k<j;k++)

{

n=Getmin(i,k)+Getmin(k+1,j)+a[i]*a[k+1]*a[j+1];

if(n<min)

min=n;

}

m[i][j]=min;

return min;

}

int main()

{

int n,i,end;

while(cin>>n)

{

if(n==0)

break;

for(i=1;i<=n;i++)

cin>>a[i]>>end;

a[i]=end;//要给最后一个n+1的那个数组赋值

memset(m,-1,sizeof(m));//初始化

cout<<Getmin(1,n)<<endl<<endl;//计算获取乘法次数最小的次数

}

小编13年上海交大毕业，曾经在小公司待过，也去过华为、OPPO等大厂，18年进入阿里一直到现在。

深知大多数初中级前端工程师，想要提升技能，往往是自己摸索成长或者是报班学习，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！
因此收集整理了一份《2024年Web前端开发全套学习资料》送给大家，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友，同时减轻大家的负担。

动态规划：矩阵连乘问题，字节跳动今日学习内容,2024年程序员面试,动态规划,矩阵,学习