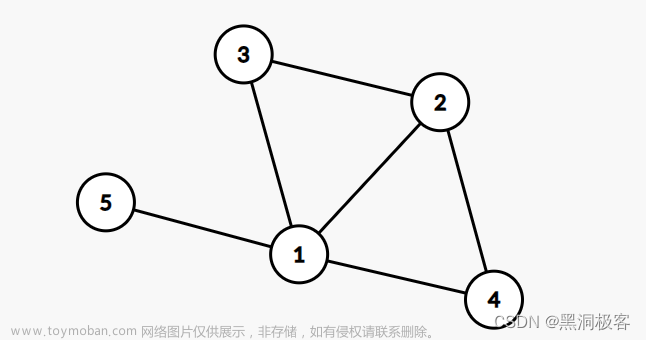
一、建图
图是由节点(v)和边(e)组成的,把图记作二元组G=(v,e)
1、基本概念
无向图 有向图
边是双向的,v1可以到v2,v2也能到v1 边是单向的,v1可以到v2,但v2不能到v1


无权图 有权图
所有边的权重都一样,都等于1 边的权重不一样,不同应用里权重的含义不一样


代码实现:
2、储存方式
无相无权图(边都是双向的,边的权重都相等)及其对应的邻接表(一种数据结构)


有向无权图及其对应的邻接矩阵


代码实现:
//邻接矩阵初始化
for(int i=1;i<=n1;i++) //n1为数组第一维大小
{
for(int j=1;j<n2;j++) //n2为数组第二维大小
{
g[i][j]=g[j][i]=0;
}
}
//储存邻接矩阵数据
cin>>n>>m; //n表示点的数量,m表示边的数量
for(int i=1;i<=m;i++) //枚举输入边
{
cin>>x>>y>>z;
dis[x][y]=z; //有向边
dis[x][y]=dis[y][x]=z; //无向边
}二、最短路
1、Dijkstra(取最短)
算法原理

以①为起点,先假设到所有节点的距离都是正无穷,依次向与之相连的②和③计算,到②的距离是3,比正无穷小,则距离更新为3,到③的距离是4,此时将①标记(已经访问过了);接着将②与③对比,到②的距离更小,则以②为起点,接着访问与②相邻的节点(不访问已经标记过的),更新距离,更新完后将②标记,以此类推,直到所有节点距离更新完毕,所有节点都被访问过为止。
该算法只适用于非负权图,如果边的权重是负数的话,用这个算法算出来的结果是错误的。
代码实现
#include <iostream>
using namespace std;
const int inf=0x7fffffff; //定义inf为无穷大
int n,e,s; //n个点,e条边,s是原点
int dis[101],check[101]; //距离,有没有被标记过
int graph[101][101]; //邻接矩阵存储一个图
int main()
{
for(int i=1;i<=100;i++) //距离初始化为无穷大
{
dis[i]=inf;
}
cin>>n>>e; //读入点和边的数量
for(int i=1;i<=e;i++) //读入每一条边的数据
{
int a,b,c;
cin>>a>>b>>c;
graph[a][b]=c; //从a到b的边权是c
}
cin>>s; //读入原点
dis[s]=0; //原点到原点距离更新为0
for(int i=1;i<=n;i++) //要把所有点check一遍
{
int minn=inf,minx; //最短距离设置为无穷大,minx储存点的编号
for(int j=1;j<=n;j++) //遍历所有的点
{
if(dis[j]<minn&&check[j]==0) //距离更小且没被标记
{
minn=dis[j],minx=j; //当前最小值更新为距离,记录点的编号
}
}
check[minx]=1; //已经是最短距离了,标记它
for(int j=1;j<=n;j++) //再找一遍所有的点
{
if(graph[minx][j]>0) //这个点和最小距离的点有连边
{
if(minn+graph[minx][j]<dis[j]) //如果绕路的距离更小
{
dis[j]=minn+graph[minx][j]; //更新距离
}
}
}
}
for(int i=1;i<=n;i++) //输出每个点的距离
{
cout<<dis[i]<<" ";
}
return 0;
}
2、floyd(中间点)
算法原理


D数组代表的是两个点之间的边权(即邻接矩阵),Path数组表示终点的前一个点(比如从0到1,1为终点,它的前一个点是0)

接着我们以1作为中间点,也就是从一个点到另一个点我们都要求经过1。如果说经过1这个点的路径会比原来的路径更短,那我们就更新这条路径为最短路径,否则保留原本路径的数据。

继续递推,直到把所有的点都作为中间点更新完之后,得到的矩阵就是最短路径。
代码实现
#include <iostream>
using namespace std;
const int N=210,M=20010,inf=0x3f3f3f3f; //最多 N个节点,M条边
int n,m,q; //n个节点,m条边,q个询问
int d[N][N]; //节点之间的距离
void floyd()
{
for(int k=1;k<=n;k++) //每个节点都充当一次中间点
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
d[i][j]=min(d[i][j],d[i][k]+d[k][j]); //如果经过这个中间点的路径更短,则更新这个路径为最短路径
}
}
}
}
int main()
{
cin>>n>>m>>q; //读入节点,边,询问
for(int i=1;i<=n;i++) //初始化每个节点之间的距离为无穷大,节点本身的距离是0
{
for(int j=1;j<=n;j++)
{
if(i==j) d[i][j]=0;
else d[i][j]=inf;
}
}
while(m--) //读入图的信息
{
int a,b,c;
cin>>a>>b>>c; //节点,节点,距离
d[a][b]=min(d[a][b],c); //如果两个节点之间不止一条路,选最小的
}
floyd();
while(q--) //询问
{
int a,b;
cin>>a>>b; //读入两个节点
if(d[a][b]>inf/2) cout<<"impossible"; //两个节点之间没有路径,输出impossible
else cout<<d[a][b]; //输出最小路径
}
return 0;
}
三、最小生成树
树的概念是所有节点都不孤立,但又不形成闭环。
1、Kruskal(权值从小到大排列)
算法原理

先将所有的点和边取出,放入一个列表中,再按边权值从小到大排列


再按照边的权值每次取出一条边回贴到图中,每回贴一条边,都要判断是否形成闭环,如果没有形成环,那这条边就选入最小生成树,如果形成了环,这条边就丢弃,继续回贴下一条边。

直到选择了n-1条边,则最小生成树已经构建完成
代码实现
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int maxn=222222;
int N,M; //顶点和边的个数
int ans=0; //最小生成树边权之和
int Num_Edge=0; //最小生成树当前边数
int father[maxn]; //并查集
struct edge{
int u,v,cost; //两个端点和他们边的权值
}E[maxn]; //最多有maxn条边
bool cmp(edge a,edge b) //自定义升序函数
{
return a.cost<b.cost; //边的权值从小到大排序
}
int findFather(int x) //查询顶点+路径压缩
{
if(father[x]!=x) father[x]=findFather(father[x]);
return father[x];
}
void kruskal()
{
for(int i=1;i<=N;i++) //并查集初始化
{
father[i]=i;
}
sort(E,E+M,cmp); //按边权从小到大排序
for(int i=0;i<=M;i++) //枚举所有边
{
if(findFather(E[i].u)!=findFather(E[i].v)) //若不在一个集合中
{
father[findFather(E[i].u)]=findFather(E[i].v); //合并集合
ans+=E[i].cost; //边权之和增加
++Num_Edge; //当前生成树边数增加
if(Num_Edge==N-1) break; //边数等于顶点数-1,跳出
}
}
if(Num_Edge==N-1) cout<<ans; //返回最小生成树边权之和
else cout<<"-1"; //无法连通时返回-1
}
int main()
{
cin>>N>>M;
for(int i=0;i<M;i++)
{
cin>>E[i].u>>E[i].v>>E[i].cost;
}
kruskal();
return 0;
}
2、Prim(两个区域间的最短路)
算法原理


node表示节点,selected表示概念是否被选入最小生成树,mindist表示从原点到该点的距离,parent表示当前点的上一个节点。
先将原点加入最小生成树最为顶点,扫描这个点连接的边,如果边的权值小于列表中的值,则将权值输入到列表里更新数据,接着扫描列表,找到最小权值,将这条边连接的节点纳入最小生成树,以这个点为新的顶点,进行下一轮更新。
 文章来源:https://www.toymoban.com/news/detail-848763.html
文章来源:https://www.toymoban.com/news/detail-848763.html
直到已选顶点的集合包括了所有的节点,最小生成树构建完毕。文章来源地址https://www.toymoban.com/news/detail-848763.html
代码实现
#include <bits/stdc++.h>
#define inf 1e8
using namespace std;
const int maxn=1005;
int graph[maxn][maxn]; //邻接矩阵
int dis[maxn]; //顶点到生成树的距离
bool vis[maxn]; //标记顶点是否已经加入生成树
int Prim(int n) //n为顶点数
{
int ans=0; //最小生成树边权之和
memset(vis,false,sizeof(vis)); //初始化
memset(dis,inf,sizeof(dis)); //初始化
dis[1]=0; //从哪个顶点开始都可以
for(int i=1;i<=n;i++)
{
int u=-1;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&(u==-1||dis[u]>dis[j]))
{
u=j; //找到最小距离的点
}
vis[u]=true; //标记该点加入生成树
ans+=dis[u];
for(int v=1;v<=n;v++)
{
if(!vis[v]&&graph[u][v]<dis[v]) //更新未加入生成树的点到生成树的距离
{
dis[v]=graph[u][v];
}
}
}
}
return ans;
}
int main()
{
int n,m;
cin>>n>>m; //顶点和边数
memset(graph,inf,sizeof(graph)); //初始化
for(int i=1;i<=m;++i)
{
int u,v,w;
cin>>u>>v>>w; //读入边权
graph[u][v]=graph[v][u]=w; //更新邻接矩阵
}
int ans=Prim(n); //计算最小生成树的权值和
cout<<ans<<endl;
return 0;
}
到了这里,关于C++学习笔记——图论的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





![[图论]哈尔滨工业大学(哈工大 HIT)学习笔记32-39](https://imgs.yssmx.com/Uploads/2024/02/720741-1.png)
![[图论]哈尔滨工业大学(哈工大 HIT)学习笔记23-31](https://imgs.yssmx.com/Uploads/2024/02/837083-1.png)