前言
本博客是博主用于复习数据结构以及算法的博客，如果疏忽出现错误，还望各位指正。
有向无环图的概念
昨天复习了拓扑排序，打算写个博客，一翻数据结构的书到那，发现连着概念还有DAG图以及AOV网，于是看了看，这篇博客先来介绍有向无环图DAG。
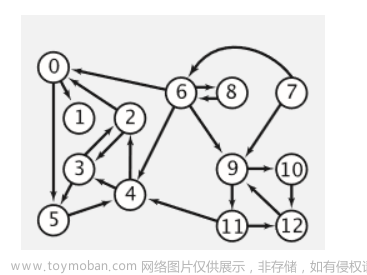
下图一个无环的有向图乘坐有向无环图，也就是DAG图。
然后发现看书看不下去，有点复杂，这书上的表达式是怎么变过去的呢？又去看了看王道的视频，发现之前好像刷王道的视频没刷到过这个DAG描述表达式。
我们学过数据结构的都知道，一个表达式可以用树来表示。
就比如说这个，然而我们观察右边那两堆子树，发现它们一模一样，于是我们就可以对它们进行一个“合并”操作。
“合并”之后，变成这样，然后虽然进行了一次合并，但是还存在着很多类似的冗余子树，比如圈出来的，再比如左边那个圈旁边的俩b，也是冗余的，再化简化简化简……就变成了书上最终的样子，amazing！
得到最终的DAG图，就是这样。
这好像也是一类题，正好可以水一篇博客。
DAG描述表达式
具体的解题步骤，就是先按照运算顺序对表达式进行分割，先后顺序有些许出入无伤大雅。就比如我写的是王道的化简步骤。
按照我自己的习惯来，就是先算最里面的括号，然后平级括号消消消。
最后应该也是可以建好的，所以先后顺序有点出入无所谓，重要的是做对题。
然后把每个结点写到最底下，这个表达式就出现过abcde，先写上。
然后按照刚才的顺序建好树，不过注意要分层！看图理解分层的意思吧，我也说不清……
然后就从最底下一层找，发现3个+指着C和D，直接合并
再看这一层没有了往上，右边那俩*，一个+，一个E，合并！（看左右是一样就合并）。
这就是最终的了，因为再往上一层，左边+右边*，再往右没了，再往上也是，这就是分层的好处。
这种方法，王道说，应该可以解决99%的，如果发现解决不了的，请去评论区留言。
好了，做道题，应该看得懂吧，选A，秒了。文章来源：https://www.toymoban.com/news/detail-848787.html
文章来源地址https://www.toymoban.com/news/detail-848787.html
到了这里，关于（Java）数据结构——图（第八节）有向无环图（DAG图）以及DAG描述表达式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
