【熟肉】线性代数的本质 - 00 - “线性代数的本质”系列预览
【熟肉】线性代数的本质 - 00 - “线性代数的本质”系列预览_哔哩哔哩_bilibili
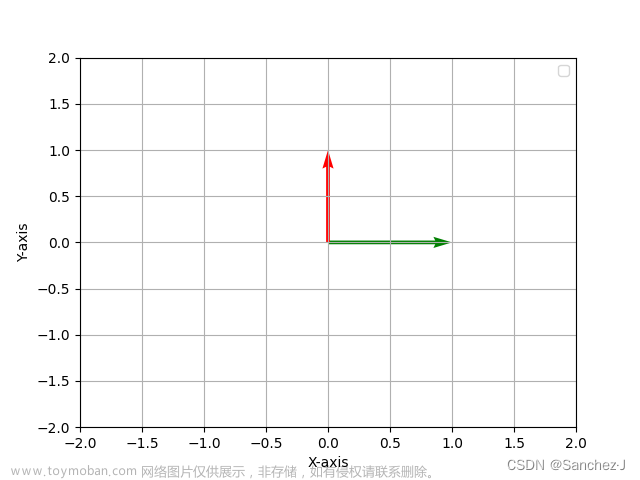
【熟肉】线性代数的本质 - 01 - 向量究竟是什么?
【熟肉】线性代数的本质 - 01 - 向量究竟是什么?_哔哩哔哩_bilibili
【熟肉】线性代数的本质 - 02 - 线性组合、张成的空间与基
【熟肉】线性代数的本质 - 02 - 线性组合、张成的空间与基_哔哩哔哩_bilibili
【熟肉】线性代数的本质 - 03 - 矩阵与线性变换
【熟肉】线性代数的本质 - 03 - 矩阵与线性变换_哔哩哔哩_bilibili
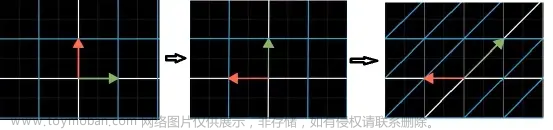
【熟肉】线性代数的本质 - 10 - 特征向量与特征值
【熟肉】线性代数的本质 - 10 - 特征向量与特征值_哔哩哔哩_bilibili
【官方双语/合集】线性代数的本质 - 系列合集
【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili
【英文讲解 中文字幕】 线性代数的本质-3Blue1Brown
【英文讲解 中文字幕】 线性代数的本质-3Blue1Brown_哔哩哔哩_bilibili
【汉语配音】比微积分恢宏,比数论精彩,跟几何浑然一体
【汉语配音】比微积分恢宏,比数论精彩,跟几何浑然一体,近代数学大厦的主殿,人工智能和广相的数学基础--四小时遍历线性代数本质,一览浩瀚乾坤【3B1B】【锦南】_哔哩哔哩_bilibili
线性代数的本质01@三蓝一棕(中文语音版)
线性代数的本质01@三蓝一棕(中文语音版)_哔哩哔哩_bilibili
线性代数的本质02向量@三蓝一棕(中文语音版)
线性代数的本质02向量@三蓝一棕(中文语音版)_哔哩哔哩_bilibili
强推!《线性代数的本质》这可能是全网把线性代数讲的最清楚的教程了吧!太强了!
强推!《线性代数的本质》这可能是全网把线性代数讲的最清楚的教程了吧!太强了!真是通俗易懂!——(高等数学基础、深度学习、机器学习、机器学习算法、OpenCV)_哔哩哔哩_bilibili
【汉语配音】线性代数的本质-系列合集-第二集:向量究竟是什么?【锦南】
【汉语配音】线性代数的本质-系列合集-第二集:向量究竟是什么?【锦南】_哔哩哔哩_bilibili
什么是向量?物理学生眼中的向量和计算学生眼中的向量有什么不同
什么是向量?物理学生眼中的向量和计算学生眼中的向量有什么不同_哔哩哔哩_bilibili
3Blue1Brown
3Blue1Brown视频专辑-3Blue1Brown视频合集-哔哩哔哩视频



【官方视频教程】《普林斯顿微积分读本》48课时(新增英字幕)
【官方视频教程】《普林斯顿微积分读本》48课时(新增英字幕),高数入门|本科衔接|考研复习|教师备课,一起肝爆微积分!_哔哩哔哩_bilibili
《普林斯顿微积分读本(修订版)》官方中文视频课程来啦!宋浩老师领衔授课
《普林斯顿微积分读本(修订版)》官方中文视频课程来啦!宋浩老师领衔授课,拯救你的高数焦虑!_哔哩哔哩_bilibili
使用Python学习高等数学(普林斯顿微积分读本)
使用Python学习高等数学(普林斯顿微积分读本)_哔哩哔哩_bilibili
【合集】《普林斯顿数学分析读本》前三章
【合集】《普林斯顿数学分析读本》前三章_哔哩哔哩_bilibili
很水的数学分析(整整300课时(更新中)!清华学长的超详细保姆式教学,学霸慎入)
很水的数学分析(整整300课时(更新中)!清华学长的超详细保姆式教学,学霸慎入)_哔哩哔哩_bilibili
【官方视频教程】《普林斯顿概率论读本》(新增英字幕)
【官方视频教程】《普林斯顿概率论读本》(新增英字幕),高数入门|本科衔接|考研复习|教师备课,一起肝爆概率论!_哔哩哔哩_bilibili
文章来源地址https://www.toymoban.com/news/detail-848842.html
【数学博士生推荐数学书】10本很好的数学分析教材!一定有一本适合你!值得一看!
【数学博士生推荐数学书】10本很好的数学分析教材!一定有一本适合你!值得一看!_哔哩哔哩_bilibili
李逸 教授个人主页
数学学院
【PDF】USTC基础数学修课指南
https://dl.icdst.org/pdfs/files3/91fd86c3c11da17c96114187b1aebf85.pdf
40、ustc_数学科学院学习指南 第2版 70页 文字版.pdf
https://download.csdn.net/download/dllglvzhenfeng/28706062
USTC数学分析习题1
https://download.csdn.net/download/weixin_35827671/86321743
数学分析 (B) 历年考试真题 2022 版
http://home.ustc.edu.cn/~shiyaowei040126/Analysis.pdf
数学与应用数学专业培养方案
catalog.ustc文章来源:https://www.toymoban.com/news/detail-848842.html
到了这里,关于线性代数的本质、普林斯顿数学三剑客等的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!