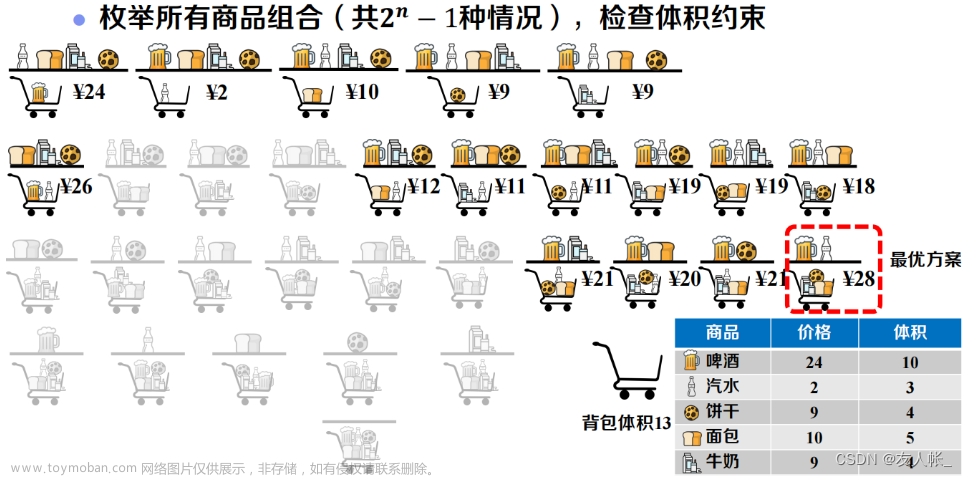
01背包

定义dp[i][j]:在前i件物品中选出若干件,放入容量为j的背包,能获得的最大价值。
考虑第i件物品拿还是不拿。讨论c[i]与背包容量的关系:
(1)j < c[i] 时,背包容量为j,而第i件物品重量大于j只能选择不拿:f[i][j] = f[i-1][j]
( 2) j >= c[i] 时,背包可以拿可以不拿第i个物品。如果选择第i件物品,那么选择第i件物品后剩余的背包容量 即从前i-1个物品选出若干个物品,放入容量为j-w[i]的背包,即f[ i-1 ][ j - w[i] ]是从前i-1个物品选出若干个物品,放入容量为j-w[i]的背包,能获得的最大价值)
拿:f[i][j]=f[i-1][j - w[i]]+c[i]
不拿:f[i][j] =f[i-1][j]
取两者最大值:f[i][j] = max( f[i-1][j-w[i]] + c[i] , f[i-1][j] )
01背包问题:
dp[n+1][m+1]
memset(dp,0,sizeof(dp));//初始化,将dp全部赋0(不用恰好装满)
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(j<w[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]= max(dp[i-1][j-w[i]]+c[i],dp[i-1][j]);
cout<<dp[n][m];只存一行数据来进行空间优化。当前结果来自上一行的j已经前面的区域(红色区域),所以必须让j以递减的形式更新,以保证能够取到上一行前面的值

因为j递减更新,用到前面的值是没优化前上一行的旧值,我们恰恰需要上一行的旧值。



优化后的代码:
for(int i=1;i<=N;i++)
for(int j=V;j>=c[i];j--)
dp[j]=max(dp[j-c[i]]+w[i],dp[j]);
cout<<dp[V];优化后的dp循环时不用分类讨论是因为:j逆序遍历,同时结束条件为j>=w[i],这两点保证了j-w[i]一定会大于0,所以不用分类讨论。但是没优化前,j正序遍历,j-w[i] 可能小于0,这将会导致没有意义以及数组越界,所以要分类讨论。
01背包方案数
容量V,N件物品,体积为C[i],价值为w[i], 求将背包(恰好)装满的方案数
定义dp[i][j]:前i件物品中选若干件放入剩余空间为j的背包中刚好把背包装满的方案总数。
考虑第i件物品能不能选
dp[i][j] = dp[i-1][j] ,0<=j<=C[i]
dp[i][j] = dp[i-1][j] + dp[i-1][j-C[i]],j>=C[i]
初始化:F[0][0]=1,即没有物品放入容量为0的背包刚好放满的方案数为1
F[0][0] = 1
for i =1 to N
do for j =0 to V
if (j < C[i])
then F[i][j] = F[i-1][j]
else
F[i][j] =F[i-1][j]+F[i-1][j-C[i]]
return F[N][V]滚动数组空间优化
F[0] =1
for i=1 to N
do for j= V to c[i]
do f[j] += f[j-c[i]];
return F[V] 多重背包问题

可以把ni个物品逐个拆分,得到ni个物品。原问题转化为01背包问题
dp[i][v] = max(dp[i-1][v-k*ci]+k*wi) ,0<=k<=ni.?
for(int i=1;i<=N;i++)
for(int j=0;j<=V;j++)
for(int k=0;k<=n[i];k++)
if(j>=c[i]*k)
dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k,dp[i][j]);
空间优化:(滚动数组 二维降一维)?
for(int i=1;i<=N;i++)
for(int j=V;j>=0;j--)
for(int k=0;k<=n[i];k++)
if(j>=c[i]*k) dp[j]=max(dp[j-c[i]*k]+w[i]*k,dp[j]);
恰好装满初始化问题
求最优解的背包问题中,有的题目要求【恰好装满背包】,有的题目并【没有要求】必须把背包装满,这两种方法初始化有所不同。设:F[i]表示容量为i的背包能够装的最大价值。
恰好装满背包:初始化:F[0] = 0 , F[i] = -INF, 1 <= i <= V。
不用恰好装满背包:初始化:F[i] = 0 , 0 <= i <= V。
初始化的F数组事实上就是在没有任何物品可以放入背包时的合法状态。
如果要求背包恰好装满:
(1) 容量为0 的背包不放入任何物品,恰好装满 ,价值为0,所以初始化为0。
(2) 容量不为0的背包不放入任何物品,不能恰好装满,所以初始化为-INF,如果求最小值,初始化为INF。循环后判断F[V]是否等于INF判断能否选出若干个物品使背包恰好装满。
如果不要求背包恰好装满:F数组全部初始化为0,因为不放入任何物品,所得的价值就是0。
完全背包问题

dp数组:dp[i][j]:表示从第一个到第i个物品任意取,背包可以装的重量为j,背包可以装的最大总价值
状态转移方程: dp[i][j]=max{ dp[i-1][j] , dp[i-1][j-k*weight[i]]+kvalue[i] }k=1,2,3....且j-k*weight>=0。
01背包问题:dp[i][j]表示从前i个物品中选出若干个物品,放入容量为j的背包中,能获得的最大价值。
状态转移方程:dp[i][j] = max(dp[i-1][j-k*w[i]]+k*c[i]) 0<=k*w[i]<= j
int dp[n+1][m+1];//下标从1开始
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
int res=-1;
for(int k=0;k*w[i]<=j;k++)
res=max(res,dp[i-1][j-k*w[i]]+k*c[i]);
dp[i][j]=res;
cout<<dp[n][m];

空间优化:


优化后的代码:
for(int i=1;i<=N;i++)
{
for(int j=c[i];j<=V;j++)
{
dp[j]=max(dp[j-c[i]]+w[i],dp[j]);
}
}
cout<<dp[V]<<endl;二维费用的背包问题

二维费用的背包问题,需要多加一维来记录
假设限制为v1,v2。dp[i][j][k]表示在前i个物品中选v1不超过j,v2不超过k的最大价值。
dp[i][j][k] = max( dp[i-1][j][k] , dp[i-1][j-v1][k-v2]+w );
空间优化:
i正序,jk逆序:
dp[j][k]=max(dp[j][k] , dp[j-v1][k-v2]+w)
#include<iostream>
using namespace std;
int N,V,M;
int dp[101][101];
int main(){
cin>>N>>V>>M;
for(int i=1;i<=N;i++){
int v,m,w;
cin>>v>>m>>w;
for(int j=V;j>=v;j--){
for(int k=M;k>=m;k--){
dp[j][k]=max(dp[j][k],dp[j-v][k-m]+w);
}
}
}
cout<<dp[V][M];
return 0;
}分组背包问题

每个组只能选一个物品,每个组的物品是互斥的。

用二维数组存数据。循环分组,逆序循环体积,正序循环一组内的选择。
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>s[i];
for(int j=0;j<s[i];j++){
cin>>v[i][j]>>w[i][j];
}
}
for(int i=0;i<n;i++){
for(int j=m;j>=0;j--){
for(int k=0;k<s[i];k++){
if(j>=v[i][k]) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
cout<<f[m]<<endl;
}
完全背包:货币系统
给你一个n种面值的货币系统,求组成面值为m的货币有多少种方案。

多重背包:LeetCode1155 掷骰子等于目标和的方法数
这里有 n 个一样的骰子,每个骰子上都有 k 个面,分别标号为 1 到 k 。给定三个整数n、k 和 target,返回投掷骰子的所有可能得到的结果,使得骰子面朝上的数字总和等于target。由于答案可能很大,需10^9+7取模。
每个筛子可以选择1~k,选择和为target。
一共n个物品,每个物品可以选择1~k个。(不可以不选,因为每个筛子至少为1)
class Solution {
public:
int K;
int N;
int t;
int dp[35][30005];
int numRollsToTarget(int n, int k, int target) {
//dp[i][j]表示从前i个筛子中恰好选择和为j的方案数
memset(dp,0,sizeof(dp));
const int mod=1e9+7;
dp[0][0]=1;
// dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+...+dp[i-1][j-k];
for(int i=1;i<=n;i++){
for(int j=1;j<=target;j++){
for(int l=1;l<=k&&j-l>=0;l++)
dp[i][j]=(dp[i][j]+dp[i-1][j-l])%mod;
}
}
return dp[n][target];
}
};01背包方案数:质数拆分
将 2019 拆分为若干个两两不同的质数之和,一共有多少种不同的方法?注意交换顺序视为同一种方法,例如 2 + 2017 = 2019 与 2017+2=2019 视为同一种方法。
在2019范围内,预处理质数数组。考虑到数组每个数可以选可以不选,然后选出的和恰好为2019的方案,转换为求01背包问题方案数。
由于是恰好组成2019,所以dp在初始化的时候要注意:dp[0]=1,dp[i]=0表示在什么都没选的情况下。从选和为0的方案数为1.其他方案数为0
for(int i=0;i<k;i++) for(int j=2019;j>=a[i];j--) dp[j]+=dp[j-a[i]];
#include <iostream>
#include<cstring>
#include<cmath>
using namespace std;
int a[2020];
bool judge(int n){
if(n==2)return true;
for(int i=2;i<int(sqrt(n))+1;i++){
if(n%i==0)
return false;
}
return true;
}
int k=0;
void init_a(){
for(int i=2;i<2019;i++){
if(judge(i))
a[k++]=i;
long long dp[2020];
int main()
{
init_a();
memset(dp,0,sizeof(dp));
dp[0]=1;
for(int i=0;i<k;i++){
for(int j=2019;j>=a[i];j--)
dp[j]+=dp[j-a[i]];
cout<<dp[2019];
return 0;
}完全背包方案数:整数划分

可以转换为完全背包问题。从1~n选择若干个数,使它们的和恰好为n,一共有多少种方案
dp[i][j]表示从前i个数选若干个数,使它们的和恰好为j的方案数。所以dp[i][j]=dp[i-1][j]+dp[i][j-i]
空间优化:
for i 1~n: for j i~n: dp[j]=dp[j]+dp[j-i]
int n;
cin>>n;
memset(dp,0,sizeof(dp));
dp[0]=1;
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++)
dp[j]=(dp[j]+dp[j-i])%mod;
cout<<dp[n];带附件的01背包:金民的采购方案

假设进行到了第i个主件,则当前一共有5种选择:(1)什么也不买(2)只买主件(3)买主件和附件1(4)买主件和附件2(5)买主件,附件1,附件2
数据结构的设计:用二维数组v[i][0],v[i][1],v[i][2]分别表示第i件主件的价值,第i件主件第一个附件的价值,第i件主件第二个附件的价值。
用二维数组w[i][0],w[i][1],w[i][2]分别表示第i件主件的重要度,第i件主件第一个附件的重要度,第i件主件第二个附件的重要度。
dp[i][j]:表示前i个主件在j的情况的最大值
dp[i][j]=max( dp[i-1][j],
dp[i-1][j-v[i][0]]+v[i][0]*w[i][0],
dp[i-1][j-v[i][0]-v[i][1]]+v[i][0]*w[i][0]+v[i][1]*w[i][1],
dp[i-1][j-v[i][0]-v[i][2]]+v[i][0]*w[i][0]+v[i][2]*w[i][2],
dp[i-1][j-v[i][0]-v[i][1]-v[i][2]]+v[i][0]*w[i][0]+v[i][1]*w[i][1]+v[i][2]*w[i][2])
int dp[32001];
int v0[61]; int p0[61]; int v1[61];
int p1[61]; int v2[61]; int p2[61];
int n,m;
int main(){
cin>>n>>m;
int v,p,q;
int cnt=1;
for(int i=1;i<=m;i++){
cin>>v>>p>>q;
if(q==0) v0[i]=v;p0[i]=p;
else if(v1[q]==-1) v1[q]=v; p1[q]=p;
else v2[q]=v; p2[q]=p;
for(int i=1;i<=m;i++)
for(int j=n;j>=v0[i]&&v0[i]!=0;j--)
if(j>=v0[i])
dp[j]=max(dp[j],dp[j-v0[i]]+v0[i]*p0[i]);
else if(j>=v0[i]+v1[i])
dp[j]=max(dp[j],dp[j-v0[i]-v1[i]]+v0[i]*p0[i]+v1[i]*p1[i]);
else if(j>=v0[i]+v2[i])
dp[j]=max(dp[j],dp[j-v0[i]-v2[i]]+v0[i]*p0[i]+v2[i]*p2[i]);
else if(j>=v0[i]+v1[i]+v2[i])
dp[j]=max(dp[j], dp[j - v1[i]- v0[i]-v2[i]]+v0[i]*p0[i]+v1[i]*p1[i]+v2[i]*p2[i]);
cout<<dp[n];
完全背包:存钱罐(恰好装满)

背包恰好装满问题:
设有n个物品,其重量(或占用空间)分别为w1, W.,...Wn.价值分别为V1,2....n. ←
给定一个总容量为W的背包,每个物品只能整个放入背包或不放。←
问:如何选择放入背包的物品,使得背包中的物品的总重恰好为W的同时,总价值最大/小?
背包恰好装满 初始化不同,最后判断是否能装满。
dp[i][j]:前i个物品恰好装满j的最小值。
恰好装满求最小值:dp->inf,dp[0]=0
恰好装满求最大值:dp->-inf,dp[0]=0
理解:
(1) 初始化是指在没有任何物品放入背包的合法状态。
①容量为0的背包可以在什么也不装的情况下恰好被装满,价值为0,所以dp[0]=0
②容量不为0的背包在什么也不装的情况下不可能被装满,属于未定义的状态,所以应该被赋无穷(具体是正无穷还是负无穷,看题目求最大值还是最小值)
(2) 当前的合法解,一定是之前的合法状态推导得到,如果循环结束后,dp[m]还是inf,说明没有合法的状态能够推导到m,说明不能从n个数中选若干个装满m。
input();
memset(dp,inf,sizeof(dp));
dp[0]=0;
int v=f-e;
for(int i=1;i<=n;i++)
for(int j=w[i];j<=v;j++)
dp[j]=min(dp[j],dp[j-w[i]]+p[i]);
if(dp[v]==inf)cout<<"impossible"<<endl;
else cout<<dp[v]<<endl;
01背包问题-二维费用:宠物小精灵之收服
- 小智拥有一定数量的精灵球(N个)和皮卡丘初始体力值(M点)。
- 每收服一只野生小精灵,会消耗特定数量的精灵球并造成对皮卡丘特定数值的体力伤害。
-
目标设定:
- 主要目标:在不超出资源限制的前提下,最大化收服的野生小精灵数量(C)。
- 次要目标(约束条件相同时):在收服相同数量野生小精灵的情况下,尽可能使皮卡丘剩余体力值最大(R)。
-
决策过程:
- 遇到每个野生小精灵时,小智有两项选择:收服或离开。
- 若选择收服,必须消耗相应数量的精灵球,皮卡丘承受相应体力伤害。
- 若选择离开,不消耗精灵球,皮卡丘无体力损失。


#include<iostream>
#include<cstring>
using namespace std;
int dp[1001][501];
int V1,V2,N;
int main(){
cin>>V1>>V2>>N;
for(int i=0;i<N;i++){
int v1,v2;
cin>>v1>>v2;
for(int j=V1;j>=v1;j--){
for(int k=V2-1;k>=v2;k--){
dp[j][k]=max(dp[j][k],dp[j-v1][k-v2]+1);
}
}
}
cout<<dp[V1][V2-1]<<" ";
for(int i=0;i<=V2-1;i++){
if(dp[V1][i]==dp[V1][V2-1]){
cout<<V2-i;
return 0;
}
}
return 0;
}leetcode 416 分割等和子集
判断一个数组能否分成两个和相等的子集。
dp[i][j]表示选前i个数和为j的方案数。
初始化:dp[0][0]=1
递推式:dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]]
空间优化:dp[j]+=dp[j-nums[i]]
01背包问题:猫狗大战
一堆数分两组(1)每组数的个数只能差一个(2)每组数之和的差值尽可能小
输入:n,n个数
输出:每组数之和
01背包:
所有数之和为sum,如果想让两组数之和相差尽可能小,那么两组数尽量靠近sum/2
数是偶数,选n/2个数,并且容量为sum/2,使价值最大。数是奇数,选n/2个数,并且容量为sum/2,是价值最大。
所以在n个数中,选n/2个数,使它们之和最大且不超过sum/2。
dp[i][j][k]:从前i个数中选k个数使它们之和不超过j并且和最大
dp[i][j][k] = max( dp[i-1][j][k],dp[i-1][j-w[i]][k-1] + w[i] )
滚动数组:
dp[j][k]=max( dp[j][k],dp[j-w[i]][k-1] + w[i] )
#include<iostream>
#include<cstring>
using namespace std;
int n;
int w[201];
int dp[10000][201];
int main()
{
memset(dp,0,sizeof(dp));
cin>>n;
int sum=0;
for(int i=1;i<=n;i++){
cin>>w[i];
sum+=w[i];
}
for(int i=1;i<=n;i++)
{
for(int j=sum/2;j>=w[i];j--){
for(int k=1;k<=n/2;k++){
dp[j][k]=max(dp[j][k],dp[j-w[i]][k-1]+w[i]);
}
}
}
cout<<dp[sum/2][n/2];
}
背包问题输出方案:机器分配 ??

如果背包问题要输出方法则不能滚动数组化简空间,因为要回溯到上一个状态,所以上一个状态不能被更新。回溯关键:判断dp[i][j]的上一步是什么。即查找dp[i][j]=dp[i-1][j-v]+w。
找到后j-=v;并break。 ???

#include<iostream>
#include<cstring>
using namespace std;
int G[11][16];
int dp[20][20];
int way[20];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>G[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=m;j>=0;j--){
int r=0;
for(int k=0;k<=m;k++){
if(j-k>=0){
r=max(r,dp[i-1][j-k]+G[i][k]);
}
}
dp[i][j]=r;
}
}
cout<<dp[n][m]<<endl;
int j=m;
for(int i=n;i>=1;i--){
for(int k=0;j<=j;k++){
if(dp[i][j]==dp[i-1][j-k]+G[i][k]){
way[i]=k;
j-=k;
break;
}
}
}
for(int i=1;i<=n;i++){
cout<<i<<" "<<way[i]<<endl;
}
return 0;
}多重背包方案:P1077摆花


初始化:dp[0][0]=1表示前0种花选0盆有一种方案 文章来源:https://www.toymoban.com/news/detail-848843.html
空间优化:dp[j]=(dp[j]+dp[j-k])%mod;//注意k从1开始循环,因为如果k=0,就相当于把dp[i-1][j]计算了两遍文章来源地址https://www.toymoban.com/news/detail-848843.html
#include<iostream>
using namespace std;
int dp[101];
int a[101];
int main()
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
dp[0]=1;
for(int i=1;i<=n;i++)
for(int j=m;j>=0;j--)
for(int k=1;k<=a[i];k++)
if(j-k>=0) dp[j]=(dp[j]+dp[j-k])%1000007;
cout<<dp[m];到了这里,关于动态规划:背包问题合集的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!