任务描述
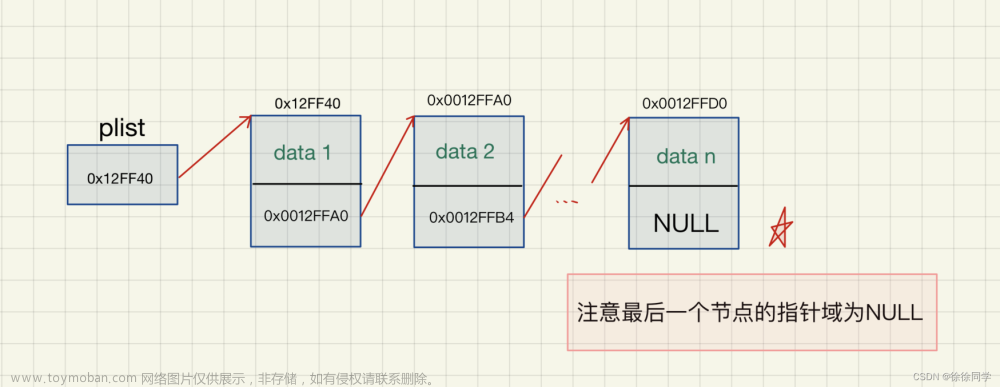
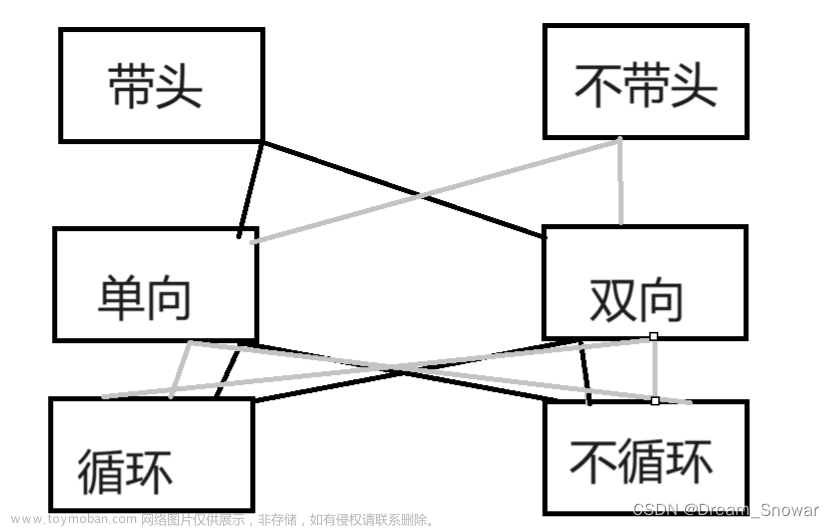
本关任务:给定两个一元多项式A(x)与B(x),利用链表表示A(x)与B(x),实现A(x)与B(x)的加法、减法、乘法和求导运算。
编程要求
输入
输入多组数据,总计n*( a+b+2)+1行。其中,第一行整数n代表总计有n组数据,之后依次输入n组数据。每组数据包括a+b+2行,其中第一行是两个整数a和b,分别代表A(x)与B(x)的项数。之后紧跟a行,每行两个整数a1和a2,分别代表A(x)每项的系数和指数,再之后紧跟b行,每行两个整数b1和b2,分别代表B(x)每项的系数和指数,每组数据最后一行为一个字符(+、-、*、'),分别代表多项式的加法、减法、乘法和求导运算。所有数据的绝对值小于100,指数大于等于0。
输出
对于每组数据输出一行,按照多项式次数从大到小排列,参考格式:5x^17+22x^7+11x^1+7。
测试说明
平台会对你编写的代码进行测试:文章来源:https://www.toymoban.com/news/detail-848967.html
测试输入: 4 1 1 1 0 1 1 + 4 3 7 0 3 1 9 8 5 17 8 1 22 7 -9 8 + 1 1 1 1 1 1 - 1 1 1 1 1 1 ' 预期输出: 1x^1+1 5x^17+22x^7+11x^1+7 0 1 1文章来源地址https://www.toymoban.com/news/detail-848967.html
#include <iostream>
#include <string>
using namespace std;
typedef struct LNode
{
int coe; //系数coe
int exp; //指数exp
struct LNode *next;
}LNode,*LinkList;
void CreatePolynomial(LinkList &L,int n)
{//按指数exp从大到小存多项式
L=new LNode;
L->next=NULL;
for(int i=0;i<n;i++)
{
LinkList p=new LNode;
cin>>p->coe>>p->exp;
LinkList pre=L,cur=L->next; //pre和cur是多项式链表的工作指针,分别初始化为头结点和首元结点
while(cur&&p->exp<cur->exp) //若待插入项的指数小于当前结点的指数,指针pre指向当前结点,当前结点的指针cur后移
{
pre=cur;
cur=cur->next;
}
p->next=cur; //待插入项的指数不小于当前结点的指数时,用头插法插入节点
pre->next=p;
}
}
void OutputPolynomial(LinkList L)
{//输出多项式
if(!L||!L->next) cout<<0;
LinkList p=L->next; //p是多项式链表的工作指针,初始化为首元结点
while(p)
{
if(p==L->next) //p指向首元结点时,根据指数的情况输出多项式
{
if (p->exp!=0)
cout<<p->coe<<"x^"<<p->exp;
else
cout<<p->coe;
}
else //p指向其他结点时,根据系数的正负和指数的情况输出多项式
{
if(p->coe>0) cout<<"+";
if(p->exp!=0)
cout<<p->coe<<"x^"<<p->exp;
else
cout<<p->coe;
}
p=p->next;
}
cout<<endl;
}
LinkList Add(LinkList LA,LinkList LB)
{//多项式的加法运算
/**************begin************/
//1.结点数据域有两个,指数与系数
/* 2.Opt(LinkList &LA,LinkList &LB,string s) 此函数调用了+、-、*和输出多项式的函数 */
// 3.return一个链表(因为有合并了的与没合并的)
LinkList LC,pa,pb,pc;//pa,pb,pc用于指出当前准备操作的结点
pa=LA->next;
pb=LB->next;
CreatePolynomial(LC,0);//需要建立LC这个链表,LinkList LC只是定义了LC指向一个结点,没有链表
pc=LC;
while(pa&&pb)//遍历比较LA与LB的结点,进行合适操作后接在LC后面
{
if(pa->exp==pb->exp)//指数相同,系数相加后存在pa中,方便接在LC后面
{
int sum=pa->coe+pb->coe;
if(sum)//判断系数和是否不为0
{
pa->coe=sum;
pc->next=pa;
pc=pa;
pa=pa->next;
pb=pb->next;
}
else
{
pa=pa->next;
pb=pb->next;
}
}
else if (pa->exp>pb->exp)//指数大的才接到LC后,pa=pa->next后继续和之前的pb->exp比较
{
pc->next=pa;
pc=pa;
pa=pa->next;
}
else {
pc->next=pb;
pc=pb;
pb=pb->next;
}
}
pc->next=pa?pa:pb;//某个链表先遍历完后,直接把另一个链表剩余部分接入LC后
return LC;
/**************end************/
}
void Minus(LinkList LA,LinkList LB)
{//多项式的减法
/**************begin************/
LinkList p=LB->next;
while(p)
{
p->coe*=-1;//减法则直接每个系数*-1然后调用刚写的Add()
p=p->next;
}
OutputPolynomial(Add(LA, LB));
/**************end************/
}
void Mul(LinkList LA,LinkList LB)
{//多项式的乘法
/**************begin************/
LinkList LC;//LC为目标多项式链表
LinkList pa=LA->next;
LinkList pb=LB->next;
CreatePolynomial(LC, 0);
LinkList temp;//记录中间结果
CreatePolynomial(temp, 0);
while(pa)//遍历比较LA与LB的结点,进行合适操作后接在LC后面
{
while(pb)//多项式乘法,就是从LA的第一个多项式起,遍历LA的同时,遍历LB的多项式并相乘
{
LinkList p=new LNode;//p是记录中间结果的辅助指针。只是一个结点,不能取代可用于Add()的temp用于LC像sun一样的循环自增
p->next=NULL;
p->coe=pa->coe*pb->coe;
p->exp=pa->exp+pb->exp;
temp->next=p;//每次两个多项式相乘的结果,暂时用p指向,然后
LC=Add(LC,temp);//pa和pb循环到最后,LC才是完全体LC。LC每次用自己加上temp,就像sum一样
pb=pb->next;
}
pb=LB->next;
pa=pa->next;
}
OutputPolynomial(LC);
/**************end************/
}
void Diff(LinkList L)
{//多项式的求导运算
LinkList p=L->next; //p是链表L的工作指针,初始化为首元结点
LinkList r=NULL; //r是删除操作的辅助指针
while(p)
{
p->coe*=p->exp;
p->exp--;
if(p->exp<0) //所有数据的指数大于等于0
{
r=p;
p=p->next;
delete r;
}
else
{
p=p->next;
}
}
OutputPolynomial(L);
}
void Opt(LinkList &LA,LinkList &LB,string s)
{//依据字符选择多项式的加法、减法、乘法和求导运算
if(s=="+") OutputPolynomial(Add(LA, LB));
if(s=="-") Minus(LA, LB);
if(s=="*") Mul(LA, LB);
if(s=="'")
{
Diff(LA);
Diff(LB);
}
}
int main()
{
int n; //总计有n组数据
cin>>n;
while(n--)
{
int a,b;
cin>>a>>b;
LinkList LA,LB;
CreatePolynomial(LA,a);
CreatePolynomial(LB,b);
string s;
cin>>s;
Opt(LA,LB,s);
}
return 0;
}到了这里,关于数据结构:链表应用:第1关:基于链表的两个一元多项式的基本运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!