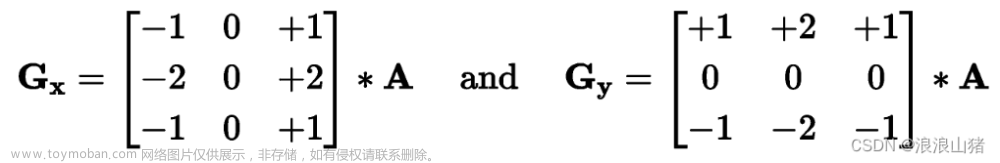python --opencv图像处理Canny算子边缘检测(Roberts算子、Prewitt算子、Sobel算子、Laplacian算子、Scharr 算子、 LOG 算子)

边缘检测

边缘检测是基于灰度突变来分割图像的常用方法，其实质是提取图像中不连续部分的特征。目前常见边缘检测算子有差分算子、 Roberts 算子、 Sobel 算子、 Prewitt 算子、 Log 算子以及 Canny 算子等。

其中， Canny 算子是由计算机科学家 John F. Canny 于 1986 年提出的一种边缘检测算子，是目前理论上相对最完善的一种边缘检测算法。

Canny 算子在 MATLAB 、 OpenCV 等常用图像处理工具中已有内置的 API。

在 OpenCV 中， Canny 算子使用的函数是 Canny() ,它的原函数如下：

def Canny(image, threshold1, threshold2, edges=None, apertureSize=None, L2gradient=None)

• image: 表示此操作的源（输入图像）。
• threshold1: 表示迟滞过程的第一个阈值。
• threshold2: 表示迟滞过程的第二个阈值。

接下来，接着操作我们之前的马里奥，对马里奥做一次边缘检测看下效果：

import cv2 as cv
from matplotlib import pyplot as plt

# 图像读入
img = cv.imread('maliao.jpg', 0)
edges = cv.Canny(img, 100, 200)

# 显示结果
titles = ['Original Img', 'Edge Img']
images = [img, edges]

# matplotlib 绘图
for i in range(2):
   plt.subplot(1, 2, i+1), plt.imshow(images[i],'gray')
   plt.title(titles[i])
   plt.xticks([]),plt.yticks([])

plt.show()

原理

滤波

在介绍原理之前，先简单的介绍下滤波，看过前面文章的可以跳过这一部分。

滤波的目的主要两个：

• 通过滤波来提取图像特征，简化图像所带的信息作为后续其它的图像处理。
• 为适应图像处理的需求，通过滤波消除图像数字化时所混入的噪声。

边缘检测就是为了简化图像，通过边缘信息来代表图像锁携带的信息。

滤波的过程可以理解为一个卷积核（3 * 3 、 5 * 5 的矩阵）在图像上，从上到下，从左到右的遍历。计算滤波器与对应像素的值并根据滤波目的进行数值计算返回值到当前像素点。

这张图蓝色块表示卷积核，滤波的过程是把图像进行点积运算并赋值到图像。

接下来的内容有些过于硬核，各位同学做好准备，我们开搞：）

Canny 算子的具体步骤

第一步：高斯滤波

高斯滤波目前是最为流行的去噪滤波算法，高斯与我们学的概率论中正态分布中正态一词指的是同一个意思，其原理为根据待滤波的像素点及其邻域点的灰度值按照高斯公式生成的参数规则进行加权平均，这样可以有效滤去理想图像中叠加的高频噪声( noise )。

第二步：计算梯度图像与角度图像

梯度图像

这里引入了一个梯度( gradient )的概念，梯度是人工智能( artificial intelligence )非常重要的一个概念，遍布机器学习、深度学习领域，我们从一阶微分方程开始，下面是一维函数的一阶微分方程的定义：

这一大串，人都看晕了对吧，实际上反应在几何图像上就是求一个函数的曲线上的切线斜率，比如下面这张图：

图像的滤波一般是基于灰度图进行的，因此图像此时是二维的，因此我们在看一下二维函数的微分，即偏微分方程：

实际上偏微分方程的几何定义就是一阶微分方程的斜切率的变化率。

那么放在图像领域，图像的梯度就是当前所在的像素点，对于 x 轴和 y 轴的偏导数，也就是二阶导数，实际上就是图像当前像素点在 x 轴和 y 轴的斜切率的变化率，在图像领域就是像素灰度值的变化率。

来一个简单的例子：

图中我们可以看到， 100 与 90 之间相差的灰度值为 10 ，即当前像素点在 X 轴方向上的梯度为 10 ，而其它点均为 90 ，则求导后发现梯度全为 0 ，因此我们可以发现在数字图像处理，因其像素性质的特殊性，微积分在图像处理表现的形式为计算当前像素点沿偏微分方向的差值，所以实际的应用是不需要用到求导的，只需进行简单的加减运算。

角度图像

角度图像的计算则较为简单，其作用为非极大值抑制的方向提供指导，公式如下：

其计算的角度值一般会取 4 个可能的角度之一：0°、45°、90°、135°。

第三步：对梯度图像进行非极大值抑制
从上一步得到的梯度图像存在边缘粗宽、弱边缘干扰等众多问题，我们可以接着使用非极大值抑制来寻找像素点局部最大值，将非极大值所对应的灰度值置0，这样可以剔除一大部分非边缘的像素点。

C 表示为当前非极大值抑制的点， g1-4 为它的周围的 8 个像素点，图中蓝色线段表示上一步计算得到的角度图像 C 点的值，即梯度方向。

第一步先判断 C 灰度值在邻域内是否最大，如是则继续检查图中梯度方向交点 dTmp1 , dTmp2 值是否大于 C ，如 C 点大于 dTmp1 , dTmp2 点的灰度值，则认定 C 点为极大值点，置为 1 。

这一步的结果会保留一些细线条，作为候选边缘。

第四步：滞后双阈值
这一步需要两个阈值：高阈值和低阈值。

经过以上三步之后得到的边缘质量已经很高了，但还是存在很多伪边缘，因此 Canny 算法中所采用的算法为双阈值法。

• 若某一像素位置的幅值超过高阈值，该像素被保留为边缘像素。
• 若某一像素位置的幅值小于高阈值，该像素被排除。
• 若某一像素位置的幅值在两个阈值之间，该像素仅仅在连接到一个高于高阈值的像素是被保留。

根据高阈值图像中把边缘链接成轮廓，当到达轮廓的端点时，该算法会在断点的 8 邻域点中寻找满足低阈值的点，再根据此点收集新的边缘，直到整个图像闭合。

Roberts 算子

Roberts 算子，又称罗伯茨算子，是一种最简单的算子，是一种利用局部差分算子寻找边缘的算子。他采用对角线方向相邻两象素之差近似梯度幅值检测边缘。检测垂直边缘的效果好于斜向边缘，定位精度高，对噪声敏感，无法抑制噪声的影响。

1963年， Roberts 提出了这种寻找边缘的算子。 Roberts 边缘算子是一个 2x2 的模版，采用的是对角方向相邻的两个像素之差。

Roberts 算子的模板分为水平方向和垂直方向，如下所示，从其模板可以看出， Roberts 算子能较好的增强正负 45 度的图像边缘。

实现 Roberts 算子，我们主要通过 OpenCV 中的 filter2D() 这个函数，这个函数的主要功能是通过卷积核实现对图像的卷积运算：

def filter2D(src, ddepth, kernel, dst=None, anchor=None, delta=None, borderType=None)

• src: 输入图像
• ddepth: 目标图像所需的深度
• kernel: 卷积核

接下来开始写代码，首先是图像的读取，并把这个图像转化成灰度图像，这个没啥好说的：

# 读取图像
img = cv.imread('maliao.jpg', cv.COLOR_BGR2GRAY)
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

# 灰度化处理图像
grayImage = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

然后是使用 Numpy 构建卷积核，并对灰度图像在 x 和 y 的方向上做一次卷积运算：

# Roberts 算子
kernelx = np.array([[-1, 0], [0, 1]], dtype=int)
kernely = np.array([[0, -1], [1, 0]], dtype=int)

x = cv.filter2D(grayImage, cv.CV_16S, kernelx)
y = cv.filter2D(grayImage, cv.CV_16S, kernely)

注意：在进行了 Roberts 算子处理之后，还需要调用convertScaleAbs()函数计算绝对值，并将图像转换为8位图进行显示，然后才能进行图像融合：

# 转 uint8 ,图像融合
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Roberts = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

最后是通过 pyplot 将图像显示出来：

# 显示图形
titles = ['原始图像', 'Roberts算子']
images = [rgb_img, Roberts]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

Prewitt 算子

Prewitt 算子是一种一阶微分算子的边缘检测，利用像素点上下、左右邻点的灰度差，在边缘处达到极值检测边缘，去掉部分伪边缘，对噪声具有平滑作用。

由于 Prewitt 算子采用 3 * 3 模板对区域内的像素值进行计算，而 Robert 算子的模板为 2 * 2 ，故 Prewitt 算子的边缘检测结果在水平方向和垂直方向均比 Robert 算子更加明显。Prewitt算子适合用来识别噪声较多、灰度渐变的图像。

Prewitt 算子的模版如下：

在代码实现上， Prewitt 算子的实现过程与 Roberts 算子比较相似，我就不多介绍，直接贴代码了：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv.imread('maliao.jpg', cv.COLOR_BGR2GRAY)
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

# 灰度化处理图像
grayImage = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# Prewitt 算子
kernelx = np.array([[1,1,1],[0,0,0],[-1,-1,-1]],dtype=int)
kernely = np.array([[-1,0,1],[-1,0,1],[-1,0,1]],dtype=int)

x = cv.filter2D(grayImage, cv.CV_16S, kernelx)
y = cv.filter2D(grayImage, cv.CV_16S, kernely)

# 转 uint8 ,图像融合
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Prewitt = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图形
titles = ['原始图像', 'Prewitt 算子']
images = [rgb_img, Prewitt]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

从结果上来看， Prewitt 算子图像锐化提取的边缘轮廓，其效果图的边缘检测结果比 Robert 算子更加明显。

Sobel 算子

Sobel 算子的中文名称是索贝尔算子，是一种用于边缘检测的离散微分算子，它结合了高斯平滑和微分求导。

Sobel 算子在 Prewitt 算子的基础上增加了权重的概念，认为相邻点的距离远近对当前像素点的影响是不同的，距离越近的像素点对应当前像素的影响越大，从而实现图像锐化并突出边缘轮廓。

算法模版如下：

Sobel 算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用，提供较为精确的边缘方向信息。因为 Sobel 算子结合了高斯平滑和微分求导（分化），因此结果会具有更多的抗噪性，当对精度要求不是很高时， Sobel 算子是一种较为常用的边缘检测方法。

在 Python 中，为我们提供了 Sobel() 函数进行运算，整体处理过程和前面的类似，代码如下：

import cv2 as cv
import matplotlib.pyplot as plt

# 读取图像
img = cv.imread('maliao.jpg', cv.COLOR_BGR2GRAY)
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

# 灰度化处理图像
grayImage = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# Sobel 算子
x = cv.Sobel(grayImage, cv.CV_16S, 1, 0)
y = cv.Sobel(grayImage, cv.CV_16S, 0, 1)

# 转 uint8 ,图像融合
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Sobel = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图形
titles = ['原始图像', 'Sobel 算子']
images = [rgb_img, Sobel]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

Laplacian 算子

拉普拉斯（ Laplacian ）算子是 n 维欧几里德空间中的一个二阶微分算子，常用于图像增强领域和边缘提取。

Laplacian 算子的核心思想：判断图像中心像素灰度值与它周围其他像素的灰度值，如果中心像素的灰度更高，则提升中心像素的灰度；反之降低中心像素的灰度，从而实现图像锐化操作。

在实现过程中， Laplacian 算子通过对邻域中心像素的四方向或八方向求梯度，再将梯度相加起来判断中心像素灰度与邻域内其他像素灰度的关系，最后通过梯度运算的结果对像素灰度进行调整。

Laplacian 算子分为四邻域和八邻域，四邻域是对邻域中心像素的四方向求梯度，八邻域是对八方向求梯度。

在 OpenCV 中， Laplacian 算子被封装在 Laplacian() 函数中，其主要是利用Sobel算子的运算，通过加上 Sobel 算子运算出的图像 x 方向和 y 方向上的导数，得到输入图像的图像锐化结果。

import cv2 as cv
import matplotlib.pyplot as plt

# 读取图像
img = cv.imread('maliao.jpg', cv.COLOR_BGR2GRAY)
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

# 灰度化处理图像
grayImage = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# Laplacian
dst = cv.Laplacian(grayImage, cv.CV_16S, ksize = 3)
Laplacian = cv.convertScaleAbs(dst)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图形
titles = ['原始图像', 'Laplacian 算子']
images = [rgb_img, Laplacian]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

示例

边缘检测算法主要是基于图像强度的一阶和二阶导数，但导数通常对噪声很敏感，因此需要采用滤波器来过滤噪声，并调用图像增强或阈值化算法进行处理，最后再进行边缘检测。文章来源地址https://www.toymoban.com/news/detail-849337.html

最后我先使用高斯滤波去噪之后，再进行边缘检测：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv.imread('maliao.jpg')
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

# 灰度化处理图像
gray_image = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 高斯滤波
gaussian_blur = cv.GaussianBlur(gray_image, (3, 3), 0)

# Roberts 算子
kernelx = np.array([[-1, 0], [0, 1]], dtype = int)
kernely = np.array([[0, -1], [1, 0]], dtype = int)
x = cv.filter2D(gaussian_blur, cv.CV_16S, kernelx)
y = cv.filter2D(gaussian_blur, cv.CV_16S, kernely)
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Roberts = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# Prewitt 算子
kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int)
kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int)
x = cv.filter2D(gaussian_blur, cv.CV_16S, kernelx)
y = cv.filter2D(gaussian_blur, cv.CV_16S, kernely)
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Prewitt = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# Sobel 算子
x = cv.Sobel(gaussian_blur, cv.CV_16S, 1, 0)
y = cv.Sobel(gaussian_blur, cv.CV_16S, 0, 1)
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Sobel = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# 拉普拉斯算法
dst = cv.Laplacian(gaussian_blur, cv.CV_16S, ksize = 3)
Laplacian = cv.convertScaleAbs(dst)

# 展示图像
titles = ['Source Image', 'Gaussian Image', 'Roberts Image',
          'Prewitt Image','Sobel Image', 'Laplacian Image']
images = [rgb_img, gaussian_blur, Roberts, Prewitt, Sobel, Laplacian]
for i in np.arange(6):
   plt.subplot(2, 3, i+1), plt.imshow(images[i], 'gray')
   plt.title(titles[i])
   plt.xticks([]), plt.yticks([])
plt.show()

Scharr 算子

在说 Scharr 算子之前，必须要提的是前面我们介绍过的 Sobel 算子， Sobel 算子虽然可以有效的提取图像边缘，但是对图像中较弱的边缘提取效果较差。

这是由于 Sobel 算子在计算相对较小的核的时候，其近似计算导数的精度比较低，例如一个 3 * 3 的 Sobel 算子，在梯度角度接近水平或垂直方向时，其不精确性就非常明显。

因此引入 Scharr 算子。Scharr 算子是对 Sobel 算子差异性的增强，两者之间的在检测图像边缘的原理和使用方式上相同。

而 Scharr 算子的主要思路是通过将模版中的权重系数放大来增大像素值间的差异。

Scharr 算子又称为 Scharr 滤波器，也是计算 x 或 y 方向上的图像差分，在 OpenCV 中主要是配合 Sobel 算子的运算而存在的，其滤波器的滤波系数如下：

Scharr 算子在 OpenCV 中的方法原型如下：

def Scharr(src, ddepth, dx, dy, dst=None, scale=None, delta=None, borderType=None):

• src: 表示输入图像
• ddepth: 表示目标图像所需的深度，针对不同的输入图像，输出目标图像有不同的深度
• dx: 表示 x 方向上的差分阶数，取值 1 或 0
• dy: 表示 y 方向上的差分阶数，取值 1 或 0

可以看到，函数 Scharr() 和 Sobel() 是非常的相似，在使用上也是完全一样的，下面看一个示例：

import cv2 as cv
import matplotlib.pyplot as plt

img = cv.imread("maliao.jpg")
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# Scharr 算子
x = cv.Scharr(gray_img, cv.CV_16S, 1, 0) # X 方向
y = cv.Scharr(gray_img, cv.CV_16S, 0, 1) # Y 方向
absX = cv.convertScaleAbs(x)
absY = cv.convertScaleAbs(y)
Scharr = cv.addWeighted(absX, 0.5, absY, 0.5, 0)

# 显示图形
plt.rcParams['font.sans-serif']=['SimHei']

titles = ['原始图像', 'Scharr 算子']
images = [rgb_img, Scharr]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

LOG 算子

LOG （ Laplacian of Gaussian ） 边缘检测算子是 David Courtnay Marr 和 Ellen Hildreth 在 1980 年共同提出的，也称为 Marr & Hildreth 算子，它根据图像的信噪比来求检测边缘的最优滤波器。该算法首先对图像做高斯滤波，然后再求其拉普拉斯（ Laplacian ）二阶导数，根据二阶导数的过零点来检测图像的边界，即通过检测滤波结果的零交叉（ Zero crossings ）来获得图像或物体的边缘。

LOG 算子实际上是把 Gauss 滤波和 Laplacian 滤波结合了起来，先平滑掉噪声，再进行边缘检测。

LOG 算子与视觉生理中的数学模型相似，因此在图像处理领域中得到了广泛的应用。

它具有抗干扰能力强，边界定位精度高，边缘连续性好，能有效提取对比度弱的边界等特点。

常见的 LOG 算子是 5 * 5 的模板;

LOG 算子到中心的距离与位置加权系数的关系曲线像墨西哥草帽的剖面，所以 LOG 算子也叫墨西哥草帽滤波器。

import cv2 as cv
import matplotlib.pyplot as plt

# 读取图像
img = cv.imread("maliao.jpg")
rgb_img = cv.cvtColor(img, cv.COLOR_BGR2RGB)

gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 先通过高斯滤波降噪
gaussian = cv.GaussianBlur(gray_img, (3, 3), 0)

# 再通过拉普拉斯算子做边缘检测
dst = cv.Laplacian(gaussian, cv.CV_16S, ksize=3)
LOG = cv.convertScaleAbs(dst)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图形
titles = ['原始图像', 'LOG 算子']
images = [rgb_img, LOG]

for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

小结

边缘检测算法主要是基于图像强度的一阶和二阶导数，但导数通常对噪声很敏感，因此需要采用滤波器来过滤噪声，并调用图像增强或阈值化算法进行处理，最后再进行边缘检测。

到了这里，关于python --opencv图像处理Canny算子边缘检测(Roberts算子、Prewitt算子、Sobel算子、Laplacian算子、Scharr 算子、 LOG 算子)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！