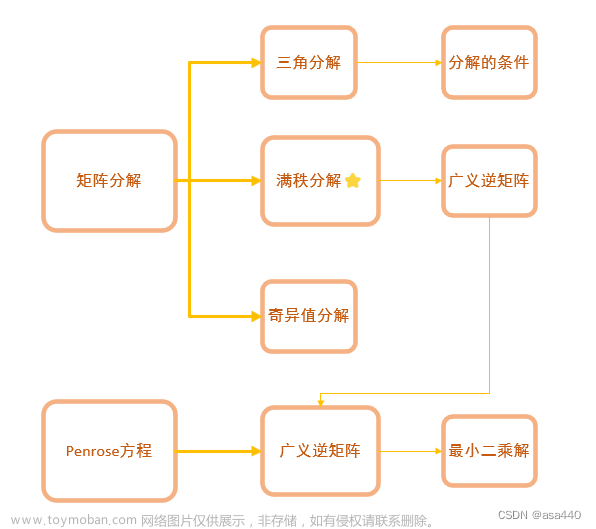
在 n n n维欧几里得空间 V V V中,有子空间 W W W. 如果用自然基 ( e i ) 1 ≤ i ≤ n (\mathbf{e}_i)_{1\leq i \leq n} (ei)1≤i≤n,设 W = s p a n ( w 1 , … , w d ) ( 0 < d < n ) W=\mathrm{span}(w_1, \ldots, w_d)\; (0< d < n) W=span(w1,…,wd)(0<d<n). 将这个基作Schmidt正交化(并单位化),得到 W W W的一个标准正交基 ( η 1 , … , η d ) (\eta_1, \ldots, \eta_d) (η1,…,ηd). 将这个标准正交基扩充为 V V V的一个基: ( η 1 , … , η d , η d + 1 , η d + 2 , … , η n ) . (\eta_1, \ldots, \eta_d, \eta_{d+1}, \eta_{d+2}, \ldots, \eta_{n}). (η1,…,ηd,ηd+1,ηd+2,…,ηn).
假定从自然基到上述标准正交基的过渡矩阵为 T T T: 即 ( η 1 , … , η d , η d + 1 , … , η n ) = ( e 1 , … , e n ) T . (\eta_1, \ldots, \eta_d, \eta_{d+1}, \ldots, \eta_{n})=(\mathbf{e_1, \ldots, e_n})\,T. (η1,…,ηd,ηd+1,…,ηn)=(e1,…,en)T.由于自然基排成的矩阵是单位方阵 I n I_n In, 所以 T T T的前 d d d列是 ( η 1 , … , η d ) (\eta_1, \ldots, \eta_d) (η1,…,ηd), 并且 T T T是正交矩阵。
命题:在 V V V的自然基之下,从 V V V(沿着 W ⊥ W^\perp W⊥)到 W W W的正交投影的矩阵是 P W = ( η 1 , η 2 , … , η d ) ( η 1 ⊤ η 2 ⊤ ⋮ η d ⊤ ) P_W=(\eta_1, \eta_2, \ldots, \eta_d)\begin{pmatrix} \eta_1^\top \\ \eta_2^\top \\ \vdots \\ \eta_d^\top \end{pmatrix} PW=(η1,η2,…,ηd) η1⊤η2⊤⋮ηd⊤ . 而在标准正交基 ( η 1 , … , η n ) (\eta_1, \ldots, \eta_n) (η1,…,ηn)之下, 从 V V V到 W W W的正交投影矩阵是 Q W = ( I d 0 ) Q_W=\begin{pmatrix} I_d & \\ & \mathbf{0} \end{pmatrix} QW=(Id0). 有等式 Q w = T − 1 P W T = T ⊤ P W T Q_w = T^{-1}P_W T=T^\top P_W T Qw=T−1PWT=T⊤PWT.
注:验证 T Q W T ⊤ = P W TQ_W T^\top = P_W TQWT⊤=PW比较容易。文章来源:https://www.toymoban.com/news/detail-849381.html
例: V = R 3 , w = ( 1 , 2 , 3 ) ⊤ , W = s p a n ( w ) V=\mathbb{R}^3, w=(1,2,3)^\top, W=\mathrm{span}(w) V=R3,w=(1,2,3)⊤,W=span(w). 则 η = 1 14 ( 1 , 2 , 3 ) ⊤ \eta=\frac{1}{\sqrt{14}}(1,2,3)^\top η=141(1,2,3)⊤. 等式 T Q W T ⊤ = P W TQ_W T^\top = P_W TQWT⊤=PW是 ( 1 14 ∗ ∗ 2 14 ∗ ∗ 3 14 ∗ ∗ ) ( 1 0 0 ) ( 1 14 2 14 3 14 ∗ ∗ ∗ ∗ ∗ ∗ ) = 1 14 ( 1 2 3 2 4 6 3 6 9 ) . \begin{pmatrix} \frac{1}{\sqrt{14}} & * & * \\ \frac{2}{\sqrt{14}} & * & * \\ \frac{3}{\sqrt{14}} & * & * \\ \end{pmatrix}\begin{pmatrix}1 & & \\ & 0 & \\ & & 0 \end{pmatrix}\begin{pmatrix}\frac{1}{\sqrt{14}} & \frac{2}{\sqrt{14}} & \frac{3}{\sqrt{14}} \\ * & * & * \\ * & * & * \end{pmatrix}=\frac{1}{14}\begin{pmatrix}1 & 2 & 3\\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{pmatrix}. 141142143∗∗∗∗∗∗ 100 141∗∗142∗∗143∗∗ =141 123246369 .文章来源地址https://www.toymoban.com/news/detail-849381.html
到了这里,关于正交投影的矩阵(基变换与过渡矩阵的例子)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!