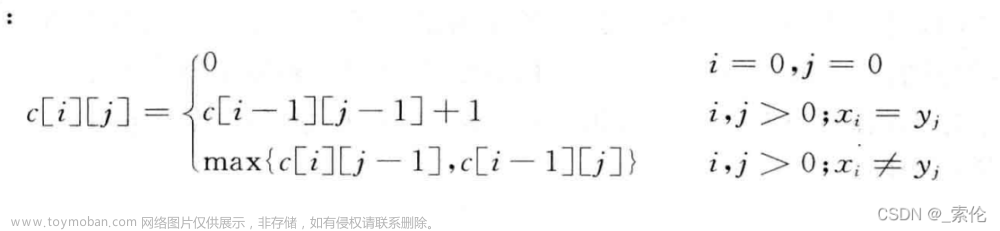动态规划—— 最长上升子序列模型解题记录-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划—— 最长上升子序列模型解题记录。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一些想法：

现在是2024-3-15 06:01:22 哈哈卷死我可爱的舍友们~ 这两天又想起来开学的时候立下的刷完kuangbin专题的flag（快进到干不完）总是先把Acwing的提高课看完吧每天这样干一点总能干完的hhhhh，这会在喝npy买的奶茶，超多椰果真的好喝爱了爱了。

解题报告：

今天是最长上升子序列模型，模型本身难度不高，利用yxc的解题方法就可以分解为以下条件：

1. 集合表示方法： f[i] 表示从这一序列的第一项到第 i 项为止的所有可能的方案。

2. 集合表示属性：长度的最大值总和的最大值

最核心的代码如下：（按照题目条件稍加修改可以过掉下面两道题）

for(int i = 1; i<=n ;i++)
{
    f[i]= 1;//赋初值 保证至少长度为1 即本身
    for(int j =1 ;j<i ;j++)
    {
        if(a[i] > a[j]) f[i] = max(f[i], f[j]+1);
    }
}

AcWing 1017. 怪盗基德的滑翔翼

AcWing 1014. 登山

然后是几道需要将原题目转化为最长上升子序列模型的题目。

合唱队形求一个带峰值的最长队伍，我们可以通过将每个人视为以他为左上升的子序列的右端点的同时视作右上升的子序列的左端点来找到最大的一个目标队形，记得减去被重复计算的这个人本身。

友好城市求最多可以批准的城市数量，思考形成最长上升子序列的过程，只有在当前考虑的一层循环的值的左边的值，即序号比它小的值才可以被考虑是否可以用来更新最大值。友好城市就是如此，我们将河岸一边的城市进行正序排序，只有当另一边的建桥方案无冲突即也是正序时才是合法方案，那么可以使用pair来保证只使用两个序号都比这一组小的值来更新最大方案。

最大上升子序列和比较简单，是对模型的变形，从求最长的子序列变成最大的子序列。

AcWing 482. 合唱队形

AcWing 1012. 友好城市

AcWing 1016. 最大上升子序列和

随后是两道剧情连续的题目。（痛苦降临）

拦截导弹。第一问就是最长上升子序列。第二问用贪心思路，从前往后扫描每个数，对每个数做判断，如果不存在比它小的数 (一个新的最大值) 那么就新开一个子序列 (新的系统)，如果存在，则找到一个结尾比它大的数列，放在这个数的后面 (可以通过二分优化) 。最后第一问输出最长的序列的长度，第二问输出创建的系统总数即可。

导弹防御系统。迭代加深，利用一个dfs参数depth来记录上升系统与下降系统的和。从depth=1开始，不断depth++直到得到一个合法的能包容上升与下降系统的和的解。

dfs过程中，暴力搜索将每个元素放到上升那一坨还是下降那一坨系统中

当满足第一个比新加入的元素的（上升或下降系统的）条件就把这个元素加进去，与上一题的贪心解法是相同的

如果没找到这样一个放入的方法的解，那么就拓宽队列的长度，直到放入上升和下降都不行的话，那么返回false

看代码会好理解一点，懒得写了（bushi）

AcWing 1010. 拦截导弹

AcWing 187. 导弹防御系统

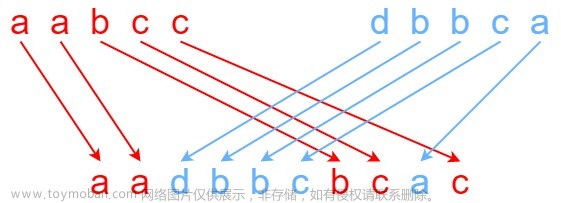
最后是一道组合题，求最长公共上升子序列。

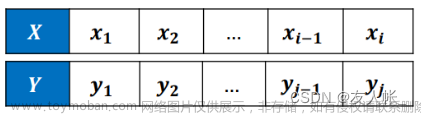
本题使用公共子序列的状态表示， f[i][j] 表示 a 的前 i 个元素中和 b 的前 j 个元素中，以b[j] 为结尾的方案，存的是方案中的上升子序列的长度的最大值。

将方案话划分为：

1. 不选 a[i] 的子集直接符合定义 f[i-1][j]

2. 选了 a[i] 的子集前提是a[i] == b[j]

然后确定最大值的转移，当 b[k] < b[j] (满足上升条件)时才能用来更新最大值，然后我们要求这些前 1~j-1 中的最大值。

时间复杂度上状态表示为状态计算为 n 所以总的时间复杂度是

注意到我们在状态计算的时候，求的来的 b[1~j] 的最大值是前缀最大值，在往后计算时会重复计算，也即最大值会在计算 b[1] 开始向后传递，同时只有当这个数已经小于我们现在正在看的 a[i] 时才能加入计算前缀最大值的行列中，所以我们开一个值 maxv ，当 a[i]>b[j] 时就记录这样的前缀最大值即可。

优化前：

for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= n; j ++ )
    {
        f[i][j] = f[i - 1][j];
        if (a[i] == b[j])
        {

            int maxv = 1;
            for (int k = 1; k < j; k ++ )
                if (b[j] > b[k])
                    maxv = max(maxv, f[i - 1][k] + 1);

            f[i][j] = max(f[i][j], maxv);
        }
    }

优化后：

    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }