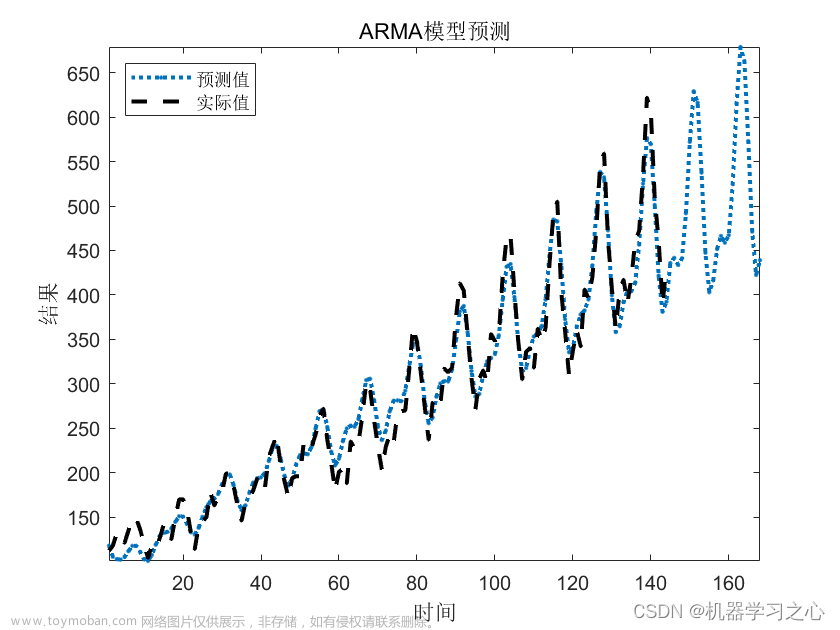
掌握ARMA模型的识别和参数估计。
原始数据在文末!!!
练习1、
根据某1915-2004年澳大利亚每年与枪支有关的凶杀案死亡率(每10万人)数据(题目1数据.txt),求:
第1小题:
(1)通过单位根检验,判断该序列的平稳性;判断该序列的纯随机性;
(2) 绘制序列的样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展;
(3)利用auto.arima()函数,对该序列进行系统自动定阶。
data <- read.table("F:/时间序列分析/实验6/习题数据/题目1数据.txt",header = T)
x <- ts(data[,2],start=1915)
#第1小题
#原序列ADF检验
library(aTSA)
adf.test(x)
#原序列白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#原序列绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)
#自动识别模型
library(zoo)
library(forecast)
#系统自动定阶
auto.arima(x)
结果分析:
第1小题:
(1)
单位根检验:检验结果显示该序列可认为是平稳序列(带漂移项无滞后模型和既有漂移项又有趋势项的无滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -1.473 0.149
[2,] 1 -1.037 0.306
[3,] 2 -0.896 0.357
[4,] 3 -0.835 0.379
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -4.54 0.0100
[2,] 1 -2.88 0.0543
[3,] 2 -2.25 0.2309
[4,] 3 -1.46 0.5330
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -4.53 0.010
[2,] 1 -2.86 0.219
[3,] 2 -2.22 0.480
[4,] 3 -1.40 0.823
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
白噪声检验:延迟6阶和延迟12阶的LB统计量的P值都小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x
X-squared = 92.781, df = 6, p-value < 2.2e-16
Box-Ljung test
data: x
X-squared = 108.89, df = 12, p-value < 2.2e-16
(2)
①自相关图可以看出,自相关系数是以一种有规律的方式,按指数函数轨迹衰减的,说明自相关系数衰减到零不是一个突然截尾的过程,而是一个连续渐变的过程,判定自相关系数拖尾;
②偏自相关图可以看出,除了1阶偏自相关系数在2倍标准差范围之外,之后几乎95%的偏自相关系数都在2倍标准差范围内,判定偏自相关系数1阶截尾;
综上所述,序列呈现出自相关系数拖尾,偏自相关系数1阶截尾的特性,初步确定拟合模型为AR(1)模型。

(3)系统自动定阶结果表明,该序列为ARMA(1,1)模型。
Series: x
ARIMA(1,0,1) with non-zero mean
Coefficients:
ar1 ma1 mean
0.9065 -0.5302 0.4616
s.e. 0.0682 0.1278 0.0591
sigma^2 = 0.01433: log likelihood = 64.48
AIC=-120.97 AICc=-120.5 BIC=-110.97
第2小题:
(1)绘制序列的时序图,判断该序列的平稳性;
(2)如果判断该序列非平稳,选择适当阶数(或步长)的差分运算。对差分后序列:做出时序图、白噪声检验、自相关图(ACF)和偏自相关图(PACF),选择适当模型拟合该差分后序列的发展(此处不要依赖系统自动定阶)
(3)选用适当估计方法确定上述拟合模型的口径。
#第2小题
#原序列时序图
plot(x)
#1阶差分
dif_x <- diff(x)
#绘制差分后序列的时序图
plot(dif_x)
#差分后序列的白噪声检验
for (i in 1:2) print(Box.test(dif_x,type = "Ljung-Box",lag = 6*i))
#绘制差分后序列的自相关图和偏自相关图
par(mfrow = c(1,2))
acf(dif_x)
pacf(dif_x)
#模型参数估计,确定模型的口径
#①选择AR(1)模型时模型的口径
arima(dif_x,order = c(1,0,0),method = "ML")
#③选择MA(3)模型时模型的口径
arima(dif_x,order = c(0,0,3),method = "ML")
结果分析:
第2小题:
- 从时序图可以看出,该序列存在明显的线性趋势,认为该序列是非平稳序列。
时序图:

- 选择1阶差分运算。
1阶差分后的时序图:从1阶差分后序列的时序图可以看出1阶差分运算后,序列在常数0附近波动,且波动有界。认为1阶差分后的序列是平稳序列。

1阶差分后序列的白噪声检验:延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则拒绝原假设,认为1阶差分后的序列不是白噪声序列。
Box-Ljung test
data: dif_x
X-squared = 21.986, df = 6, p-value = 0.001218
Box-Ljung test
data: dif_x
X-squared = 40.071, df = 12, p-value = 6.998e-05
ACF图和PACF图:
- 从自相关图看出,除了1阶自相关系数在2倍标准差范围之外,之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为1阶截尾;
- 从偏自相关图看出,除了1-3阶偏自相关系数在2倍标准差范围之外,之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为3阶截尾;
综上所述,序列呈现出自相关系数1阶截尾的特性,偏自相关系数3阶截尾的特性,初步确定拟合模型为AR(1)模型或MA(3)模型。

(3)
①选择AR(1)模型时模型的口径为:
,
该AR(1)模型的等价表达为:
,
Call:
arima(x = dif_x, order = c(1, 0, 0), method = "ML")
Coefficients:
ar1 intercept
-0.4033 -0.0037
s.e. 0.0964 0.0096
sigma^2 estimated as 0.01589: log likelihood = 57.94, aic = -109.87
- 选择MA(3)模型时模型的口径为:
,
Call:
arima(x = dif_x, order = c(0, 0, 3), method = "ML")
Coefficients:
ma1 ma2 ma3 intercept
-0.5734 -0.0495 -0.0109 -0.0033
s.e. 0.1103 0.1069 0.1067 0.0047
sigma^2 estimated as 0.01421: log likelihood = 62.79, aic = -115.58
练习2、
根据1860-1955年密歇根湖每月平均水位的最高值序列(题目2数据.csv),求:
第1小题:
(1)通过单位根检验,判断该序列的平稳性;判断该序列的纯随机性;
(2) 绘制序列的样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展;
(3)利用auto.arima()函数,对该序列进行系统自动定阶。
data <- read.csv("F:/时间序列分析/实验6/习题数据/题目2数据.csv",sep = ",",header = T)
x <- ts(data[,2],start=1860)
#第1小题
#原序列ADF检验
adf.test(x)
#原序列白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#原序列绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)
#系统自动定阶
auto.arima(x)
结果分析:
第1小题:
- 单位根检验:检验结果显示该序列可认为是平稳序列(带漂移项1阶滞后模型和既有漂移项又有趋势项的1阶滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -0.312 0.553
[2,] 1 -0.320 0.551
[3,] 2 -0.307 0.555
[4,] 3 -0.245 0.573
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -2.88 0.0535
[2,] 1 -3.39 0.0154
[3,] 2 -2.73 0.0776
[4,] 3 -2.34 0.1973
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -3.22 0.0891
[2,] 1 -4.03 0.0113
[3,] 2 -3.10 0.1204
[4,] 3 -2.60 0.3258
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
白噪声检验:延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x
X-squared = 215.96, df = 6, p-value < 2.2e-16
Box-Ljung test
data: x
X-squared = 329.2, df = 12, p-value < 2.2e-16
(2)①自相关图可以看出,自相关系数是以一种有规律的方式,按指数函数轨迹衰减的,说明自相关系数衰减到零不是一个突然截尾的过程,而是一个连续渐变的过程,判定自相关系数拖尾;
②偏自相关图可以看出,除了1阶偏自相关系数在2倍标准差范围之外,之后几乎95%的偏自相关系数都在2倍标准差范围内,判定偏自相关系数1阶截尾;
综上所述,序列呈现出自相关系数拖尾,偏自相关系数1阶截尾的特性,初步确定拟合模型为AR(1)模型。

(3)利用auto.arima()函数,对该序列进行系统自动定阶:
Series: x
ARIMA(0,1,0)
sigma^2 = 0.4751: log likelihood = -99.44
AIC=200.87 AICc=200.92 BIC=203.43
第2小题:
(1)绘制序列的时序图,判断该序列的平稳性;
(2)如果判断该序列非平稳,选择适当阶数(或步长)的差分运算。对差分后序列:做出时序图、白噪声检验(延迟3阶和6阶)、自相关图(ACF)和偏自相关图(PACF),选择适当模型拟合该差分后序列的发展(此处不要依赖系统自动定阶)
(3)选用适当估计方法确定上述拟合模型的口径。
#第2小题
#原序列时序图
plot(x)
#1阶差分
dif_x <- diff(x)
#绘制差分后序列的时序图
plot(dif_x)
#差分后序列的白噪声检验
for (i in 1:2) print(Box.test(dif_x,type = "Ljung-Box",lag = 3*i))
#绘制差分后序列的自相关图和偏自相关图
par(mfrow = c(1,2))
acf(dif_x)
pacf(dif_x)
#模型参数估计,确定模型的口径
arima(dif_x,order = c(2,0,2),method = "ML")
第2小题:
(1)从时序图可以看出,该序列存在明显的线性趋势,认为该序列是非平稳序列。
时序图:

(2)选择1阶差分运算。
1阶差分后的时序图:从1阶差分后序列的时序图可以看出1阶差分运算后,序列在常数0附近波动,且波动有界。认为1阶差分后的序列是平稳序列。

1阶差分后序列的白噪声检验:延迟3阶的LB统计量的P值为0.01051小于α=0.05,但延迟6阶的LB统计量P值为0.0648,大于α=0.05,则拒绝原假设,认为1阶差分后的序列不是白噪声序列。
Box-Ljung test
data: dif_x
X-squared = 11.236, df = 3, p-value = 0.01051
Box-Ljung test
data: dif_x
X-squared = 11.876, df = 6, p-value = 0.0648
ACF图和PACF图:
- 从自相关图看出,自相关系数呈现不规则地衰减到零值附近。判定为拖尾;
- 从偏自相关图看出,偏自相关系数呈现出对数函数单调收敛到零值附近。判定为拖尾特性;
综上所述,序列呈现出自相关系数拖尾的特性,偏自相关系数拖尾的特性,初步确定拟合模型为ARMA(2,2)模型。

(3)选择ARMA(2,2)模型时模型的口径为:
,
该ARMA(2,2)模型的等价表达为:

Call:
arima(x = dif_x, order = c(2, 0, 2), method = "ML")
Coefficients:
ar1 ar2 ma1 ma2 intercept
0.7210 -0.1642 -0.6746 -0.1715 -0.0189
s.e. 0.3128 0.4113 0.3091 0.4237 0.0281
sigma^2 estimated as 0.4081: log likelihood = -92.51, aic = 197.02
需要本训练原始数据请自行跳转下载:文章来源:https://www.toymoban.com/news/detail-849737.html
博文:‘ARMA模型的识别与参数估计’训练数据资源-CSDN文库文章来源地址https://www.toymoban.com/news/detail-849737.html
到了这里,关于时间序列分析 #ARMA模型的识别与参数估计 #R语言的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!