云仔☁笔记
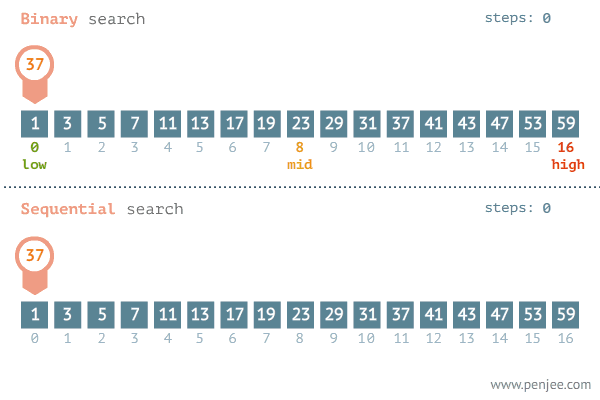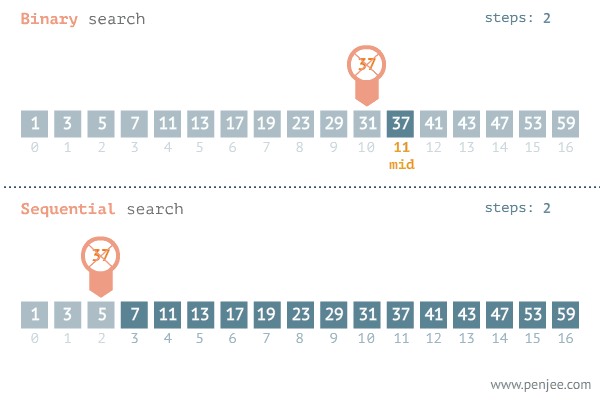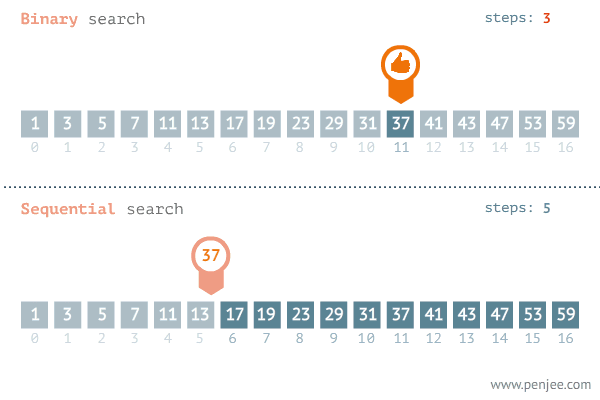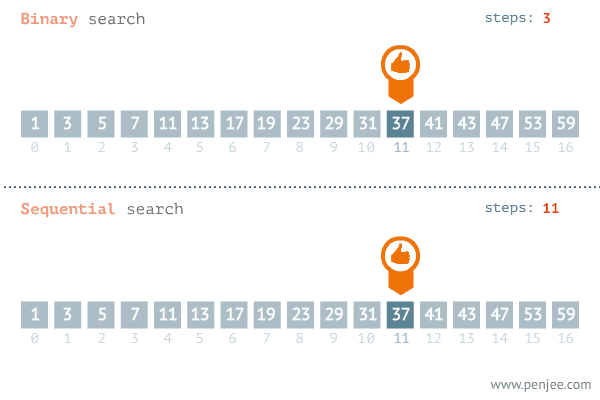
1. 基础版
左闭右闭
public static int binaryBasic(int[] arr, int target) {
int i = 0, j = arr.length - 1;
while (i <= j) {
int m = (j + i)>>>1; //一半取整
if (arr[m] < target) {//目标在右边
i = m + 1;
}else if (target < arr[m]) {//目标在左边
j = m - 1;
}else {//找到结果
return m;
}
}
//找不到,则返回-1
return -1;
}
2. 改动版
public static int binaryAlter(int[] arr, int target) {
int i = 0, j = arr.length; //改动1
while (i < j) { //改动2
int m = (j + i)>>>1;
if (arr[m] < target) {
i = m + 1;
}else if (target < arr[m]) {
j = m; //改动3
}else {//找到结果
return m;
}
}
return -1;
}
- 左闭右开,即 j 只是一个边界,不可能等于目标元素
时间复杂度
最坏情况
循环次数 L = f l o o r ( l o g 2 ( n ) + 1 ) ∗ 5 + 4 L = floor(log_2(n) + 1) * 5 + 4 L=floor(log2(n)+1)∗5+4
| 行 | 次数 |
|---|---|
i < j |
L + 1 |
int m = (j + i)>>>1; |
L |
arr[m] < target |
L |
target < arr[m] |
L |
i = m + 1 |
L |
- 最终表达式 : f l o o r ( l o g 2 ( n ) + 1 ) ∗ 5 + 4 floor(log_2(n) + 1) * 5 + 4 floor(log2(n)+1)∗5+4
- 渐进上界: O ( l o g 2 ( n ) ) O(log_2(n)) O(log2(n))
最好的情况
若待查找元素恰好在数组中央,只需要循环一次 O ( 1 ) O(1) O(1)
空间复杂度
- 需要常数个指针i,j,m,因此额外占用的空间是 O ( 1 ) O(1) O(1)
3. 平衡版
public static int binaryBalance(int[] arr, int target) {
int i = 0, j = arr.length;
while (1 < j - i) {
int m = (i + j) >>> 1;
if (target < arr[m]) { //左侧
j = m;
}else {
i = m;
}
}
if (arr[i] == target) {
return i;
}else {
return -1;
}
}
- 左闭右开的区间,i指向的可能是目标,而j指向的不是目标
- 不在循环内找出,等范围内只剩i时,退出循环,在循环外比较a[i]和target
- 与改动版相比较
- 优点:循环内的平均比较次数减少了
- 缺点:当target恰好在中间时,还是必须执行完循环
时间复杂度
Θ ( l o g ( n ) ) Θ (log(n)) Θ(log(n))
4. 在java中的实现
java.util.Arrays.binarySearch()
public static int binarySearch(int[] a, int key) {
return binarySearch0(a, 0, a.length, key);
}
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
int key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
-
可以看到java8,使用的咱们前面的基础版实现二分查找,但最终的返回结果是 -(插入索引 + 1),
源文档中对返回值的描述:
index of the search key, if it is contained in the array within the specified range; otherwise, (-(insertion point) - 1). The insertion point is defined as the point at which the key would be inserted into the array: the index of the first element in the range greater than the key, or toIndex if all elements in the range are less than the specified key. Note that this guarantees that the return value will be >= 0 if and only if the key is found.
翻译:如果搜索键包含在指定范围内的数组中,则搜索键的索引;否则,(-(插入点)- 1)。插入点定义为键插入数组的点:范围内第一个大于键的元素的索引,如果范围内所有元素都小于指定的键,则为toIndex。注意,这保证了当且仅当找到键时返回值将>= 0。
思考: 为什么要+1呢?
若不 + 1,当插入位置在数组的最前端时,得到的结果时 -0,在java中无法区分-0和0,所通过 + 1 的操作,避免了在这个问题
扩展
-
得到插入索引后,可以将目标值插入文章来源:https://www.toymoban.com/news/detail-850026.html
-
我们来实现这个过程,在java中数据的长度是不可变的,所以我们需要通过创建一个新的数组来实现这个过程文章来源地址https://www.toymoban.com/news/detail-850026.html
//定义测试数据
int[] arr = {5,6,7,12,45,67,89,95,99,102};
int target = 42;
//进行二分查找
int i = Arrays.binarySearch(arr, target);
System.out.println(i);
if (i < 0) {
//得到索引
int insertIndex = Math.abs(i + 1);
//创建新的数组,接收插入后的数据
int[] b = new int[arr.length + 1];
//使用java中的数据复制方法
System.arraycopy(arr, 0, b, 0, insertIndex);
b[insertIndex] = target;
System.arraycopy(arr, insertIndex, b, insertIndex + 1, arr.length - insertIndex);
//打印结果
System.out.println(Arrays.toString(b));
}
5. 对重复元素的处理
5.1 最左 leftMost
/**
* 最左查询
* @param arr 查询数组
* @param target 目标
* @return 若存在,返回最左索引,若不存在,返回 -(比目标值大值的最左索引+1)
*/
public static int leftMost(int[] arr, int target) {
int i = 0, j = arr.length - 1;
while (i <= j) {
int m = (j + i)>>>1;
if (target <= arr[m]) {
j = m - 1;
}else {
i = m + 1;
}
}
return i < arr.length && arr[i] == target ? i : -(i + 1);
}
5.2 最右rightMost
/**
* 最右
* @param arr 查询数组
* @param target 目标
* @return 若存在,返回最右索引,若不存在,返回 -(比目标值小的值的最右索引 + 1)
*/
public static int rightMost(int[] arr, int target) {
int i = 0, j = arr.length - 1;
while (i <= j) {
int m = (j + i)>>>1;
if (target < arr[m]) {
j = m - 1;
}else {
i = m + 1;
}
}
return i > 0 && i <= arr.length && arr[i - 1] == target ? i - 1 : - (i + 1);
}
6. 力扣题型练习
- 34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
- 35. 搜索插入位置 - 力扣(LeetCode)
- 704. 二分查找 - 力扣(LeetCode)
到了这里,关于二分查找的5种实现--Java版的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!