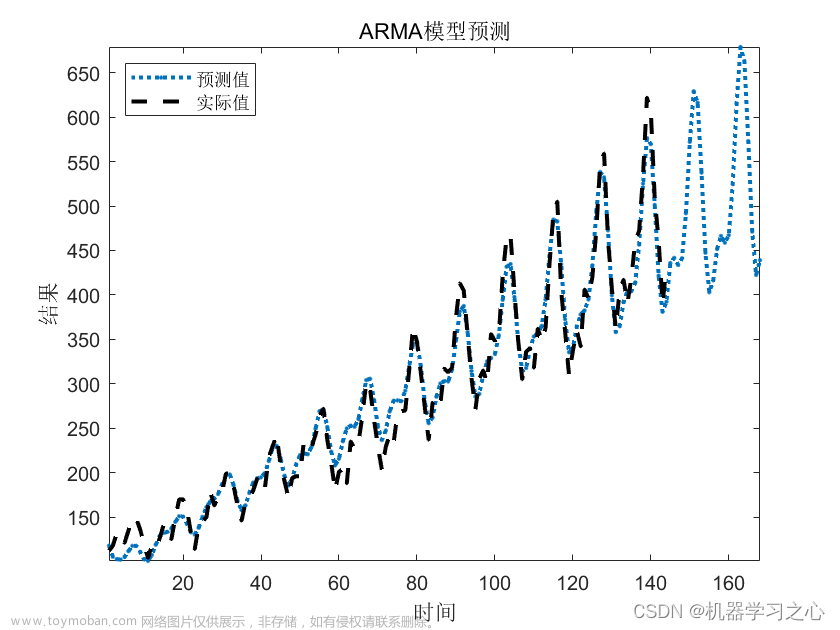
- 掌握ARMA模型检验的内容和方法
- 理解模型优化的SBC准则和BIC准则的思想与原理,能综合运用上述准则选择相对最优拟合模型
训练数据在文末!!!
练习1、根据某公司过去三年每月缴纳的税收金额(行数据)(题目1数据.txt),求
(1)绘制序列时序图,判断序列的平稳性与纯随机性;
(2)绘制序列的样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,尝试选择多个(例如AR,MA)模型拟合该序列的发展,并分别求出各个拟合模型的口径;
(3)对上述选定的拟合模型进行模型的检验;
(4)综合运用SBC准则和BIC准则,选出相对最优模型。
data <- scan("F:/时间序列分析/实验7/习题数据/题目1数据.txt")
x <- ts(data,start=c(2019,1),frequency = 12)
#原序列时序图
plot(x)
#原序列白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#原序列绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)
#模型参数估计,确定模型的口径
#①选择MA(1)模型时模型的口径
x.fit1 <- arima(x,order = c(0,0,1),method = "ML")
x.fit1
#②选择AR(2)模型时模型的口径
x.fit2 <- arima(x,order = c(2,0,0),method = "ML")
x.fit2
#模型检验
#MA(1)模型检验
ts.diag(x.fit1)
t = abs(x.fit1$coef)/sqrt(diag(x.fit1$var.coef))
pt(t,length(x)-length(x.fit1$coef),lower.tail = F)
#AR(3)模型检验
ts.diag(x.fit2)
t = abs(x.fit2$coef)/sqrt(diag(x.fit2$var.coef))
pt(t,length(x)-length(x.fit2$coef),lower.tail = F)
#模型优化,比较各模型的AIC值和BIC值
AIC(x.fit1)
AIC(x.fit2)
BIC(x.fit1)
BIC(x.fit2)
data.frame(AIC(x.fit1),AIC(x.fit2),BIC(x.fit1),BIC(x.fit2))
结果分析:
(1)时序图:从时序图可以看出,该序列在常数9附近波动,且波动有界。认为该序列是平稳序列。

白噪声检验:延迟6阶和延迟12阶的LB统计量的P值都小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x
X-squared = 25.658, df = 6, p-value = 0.0002578
Box-Ljung test
data: x
X-squared = 31.566, df = 12, p-value = 0.001614
(2)①从自相关图看出,除了1阶自相关系数在2倍标准差范围之外,之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为1阶截尾;
②从偏自相关图看出,除了1-2阶偏自相关系数在2倍标准差范围之外,之后几乎95%的自相关系数都突然衰减到2倍标准差范围之内。判定为2阶截尾;
综上所述,序列呈现出自相关系数1阶截尾的特性,偏自相关系数2阶截尾的特性,初步确定拟合模型为MA(1)模型或MA(2)模型。
ACF图和PACF图:

确定模型口径:
MA(1)模型口径:,
Call:
arima(x = x, order = c(0, 0, 1), method = "ML")
Coefficients:
ma1 intercept
1.0000 9.2118
s.e. 0.0798 0.2792
sigma^2 estimated as 0.7205: log likelihood = -46.99, aic = 99.97
AR(2)模型口径:,
该AR(2)模型的等价表达为:
,
Call:
arima(x = x, order = c(2, 0, 0), method = "ML")
Coefficients:
ar1 ar2 intercept
1.0276 -0.5412 9.1154
s.e. 0.1524 0.1738 0.2945
sigma^2 estimated as 0.7977: log likelihood = -47.65, aic = 103.31
(3)MA(1)模型检验:
模型显著性检验:因为4-24阶延迟下LB统计量的P值都显著大于0.05,接受原假设,可以认为该拟合模型的残差序列属于白噪声序列,即该拟合模型显著有效。残差Q-Q图显示,数据点基本围绕在基准线附近,不能拒绝残差项是正态的假设。

模型参数显著性检验:t统计量的P值小于α=0.05,拒绝原假设,故认为两个参数均显著非零。
ma1 intercept
1.363877e-14 1.045188e-27
AR(2)模型检验:
模型显著性检验:因为4-24阶延迟下LB统计量的P值都显著大于0.05,接受原假设,可以认为该拟合模型的残差序列属于白噪声序列,即该拟合模型显著有效。残差Q-Q图显示,数据点基本围绕在基准线附近,不能拒绝残差项是正态的假设。

模型参数显著性检验:t统计量的P值小于α=0.05,拒绝原假设,故认为两个参数均显著非零。
ar1 ar2 intercept
5.523818e-08 1.901274e-03 2.922119e-26
(4)模型优化:
用AIC准则和BIC准则评判,MA(1)和AR(2)两个拟合模型的相对优势,最小信息量检验显示,无论是使用AIC准则还是使用BIC准则,MA(1)模型都要优于AR(2)模型,在本题中MA(1)模型是相对最优模型。
AIC.x.fit1. AIC.x.fit2. BIC.x.fit1. BIC.x.fit2.
1 99.9722 103.3087 104.7228 109.6428
练习2、根据某城市过去45年中每年的人口死亡率(行数据)(题目2数据.txt),求:
(1)绘制序列时序图,判断序列的平稳性与纯随机性;
(2)绘制序列的样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,尝试选择多个(例如AR,MA,ARMA)模型拟合该序列的发展;
(3)对上述选定的拟合模型进行模型的检验;
(4)综合运用SBC准则和BIC准则,选出相对最优模型。
data <- scan("F:/时间序列分析/实验7/习题数据/题目2数据.txt")
x <- ts(data,start=1977)
#原序列时序图
plot(x)
#原序列白噪声检验
for(i in 1:2) print(Box.test(x,type = "Ljung-Box",lag = 6*i))
#原序列绘制自相关图和偏自相关图
par(mfrow = c(1,2))
acf(x)
pacf(x)
#模型参数估计,确定模型的口径
#①选择MA(1)模型时模型的口径
x.fit1 <- arima(x,order = c(0,0,1),method = "ML")
x.fit1
#③选择AR(2)模型时模型的口径
x.fit2 <- arima(x,order = c(2,0,0),method = "ML")
x.fit2
#③选择ARMA(2,1),1模型时模型的口径
x.fit3 <- arima(x,order = c(2,0,1),method = "ML")
x.fit3
#模型检验
#MA(1)模型检验
ts.diag(x.fit1)
t = abs(x.fit1$coef)/sqrt(diag(x.fit1$var.coef))
pt(t,length(x)-length(x.fit1$coef),lower.tail = F)
#AR(2)模型检验
ts.diag(x.fit2)
t = abs(x.fit2$coef)/sqrt(diag(x.fit2$var.coef))
pt(t,length(x)-length(x.fit2$coef),lower.tail = F)
#ARMA(2,1)模型检验
ts.diag(x.fit3)
t = abs(x.fit3$coef)/sqrt(diag(x.fit3$var.coef))
pt(t,length(x)-length(x.fit3$coef),lower.tail = F)
#模型优化,比较各模型的AIC值和BIC值
AIC(x.fit1)
AIC(x.fit2)
AIC(x.fit3)
BIC(x.fit1)
BIC(x.fit2)
BIC(x.fit3)
data.frame(AIC(x.fit1),AIC(x.fit2),AIC(x.fit3),BIC(x.fit1),BIC(x.fit2),BIC(x.fit3))
结果分析:
(1)时序图:从时序图可以看出,该序列在常数5附近波动,且波动有界。认为该序列是平稳序列。

白噪声检验:延迟6阶的LB统计量的P值大于α=0.05,但延迟12阶的LB统计量的P值小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x
X-squared = 10.609, df = 6, p-value = 0.1013
Box-Ljung test
data: x
X-squared = 23.893, df = 12, p-value = 0.02104
(2)①从自相关图看出,自相关系数呈现不规则地衰减到零值附近。判定为拖尾;
②从偏自相关图看出,偏自相关系数呈现出对数函数单调收敛到零值附近。判定为拖尾特性;
综上所述,序列呈现出自相关系数拖尾的特性,偏自相关系数拖尾的特性,初步确定拟合模型为ARMA(2,1)模型。
ACF图和PACF图:

确定模型口径:
MA(1)模型口径:,
Call:
arima(x = x, order = c(0, 0, 1), method = "ML")
Coefficients:
ma1 intercept
0.4495 4.9444
s.e. 0.1203 0.2020
sigma^2 estimated as 0.8857: log likelihood = -61.23, aic = 128.47
AR(2)模型口径:,
该AR(2)模型的等价表达为:
,
Call:
arima(x = x, order = c(2, 0, 0), method = "ML")
Coefficients:
ar1 ar2 intercept
0.4661 -0.3259 4.9569
s.e. 0.1412 0.1394 0.1597
sigma^2 estimated as 0.8383: log likelihood = -60.06, aic = 128.12
ARMA(2,1)模型时模型的口径为:
,
该ARMA(2,1)模型的等价表达为:
,
Call:
arima(x = x, order = c(2, 0, 1), method = "ML")
Coefficients:
ar1 ar2 ma1 intercept
0.5741 -0.3651 -0.1221 4.9586
s.e. 0.3617 0.1740 0.3847 0.1527
sigma^2 estimated as 0.8363: log likelihood = -60.01, aic = 130.02
(3)MA(1)模型检验:
模型显著性检验:因为4-24阶延迟下LB统计量的P值都显著大于0.05,接受原假设,可以认为该拟合模型的残差序列属于白噪声序列,即该拟合模型显著有效。残差Q-Q图显示,数据点基本围绕在基准线附近,不能拒绝残差项是正态的假设。

模型参数显著性检验:t统计量的P值小于α=0.05,拒绝原假设,故认为两个参数均显著非零。
ma1 intercept
2.740853e-04 3.548356e-27
AR(2)模型检验:
模型显著性检验:因为4-24阶延迟下LB统计量的P值都显著大于0.05,接受原假设,可以认为该拟合模型的残差序列属于白噪声序列,即该拟合模型显著有效。残差Q-Q图显示,数据点基本围绕在基准线附近,不能拒绝残差项是正态的假设。

模型参数显著性检验:t统计量的P值小于α=0.05,拒绝原假设,故认为三个参数均显著非零。
ar1 ar2 intercept
9.847737e-04 1.212639e-02 6.817368e-31
ARMA(2,1)模型检验:
模型显著性检验:因为4-24阶延迟下LB统计量的P值都显著大于0.05,接受原假设,可以认为该拟合模型的残差序列属于白噪声序列,即该拟合模型显著有效。残差Q-Q图显示,数据点基本围绕在基准线附近,不能拒绝残差项是正态的假设。

模型参数显著性检验:只有AR(2)和常数项的t统计量的P值小于α=0.05,拒绝原假设,故认为只有AR(2) 和常数项的参数显著非零。
ar1 ar2 ma1 intercept
6.006193e-02 2.103146e-02 3.762491e-01 3.541855e-31
(4)模型优化:
用AIC准则和BIC准则评判,MA(1)、AR(2)和ARMA(2,1)三个拟合模型的相对优势,最小信息量检验显示,使用AIC准则时AR(2)模型相对较优,使用BIC准则,MA(1)模型相对较优。
AIC.x.fit1
AIC.x.fit2
AIC.x.fit3
BIC.x.fit1
BIC.x.fit2
BIC.x.fit3
1
128.4692
128.1235
130.0208
133.8892
135.3502
139.0541
需要该练习的训练数据请自行跳转下载:文章来源:https://www.toymoban.com/news/detail-850357.html
博文:‘ARMA模型的检验与优化’训练数据资源-CSDN文库文章来源地址https://www.toymoban.com/news/detail-850357.html
到了这里,关于ARMA模型的检验与优化 #时间序列分析 R语言的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!