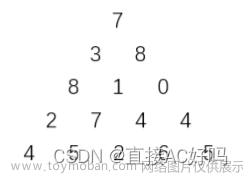
【题解 | 基础动态规划】：数字三角形-Toy模板网

这篇具有很好参考价值的文章主要介绍了【题解 | 基础动态规划】：数字三角形。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数字三角形

链接：[USACO1.5] [IOI1994]数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

【题解 | 基础动态规划】：数字三角形,# 题解记录,动态规划,算法,java,C++

在上面的样例中，从 $\to 3 \to 8 \to 7 \to 5$ 的路径产生了最大权值。

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】
对于 $100\%$ 的数据， $1\le r \le 1000$ ，所有输入在 $[0, 100]$ 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

参考代码

这道题就是很裸的DP，也是很经典的入门题。我们先用记忆化搜索写一遍，再来写DP。

（1）记忆化搜索

我们首先读取金字塔的行数 r 和每行的数字，并存储在二维数组 triangle 中。然后，我们使用记忆化搜索的深度优先搜索函数 dfs 来计算从金字塔顶部到底部的最大路径和。

在 dfs 函数中，如果已经计算过当前位置到底部的最大路径和，我们直接返回结果；如果已经到达最后一行，我们返回当前值；否则，我们返回从当前位置到底部的最大路径和，并将结果存储在记忆化搜索数组 memo 中，以便后续使用。

最后，我们输出最大路径和。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Main {
    // 快读快写
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static StreamTokenizer in = new StreamTokenizer(br);
    public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
    
    public static int[][] triangle;
    public static Integer[][] memo;  // 用于记忆化搜索的数组

    public static void main(String[] args) throws IOException {
        // 读数据
        in.nextToken();
        int r = (int) in.nval;
        triangle = new int[r][];
        memo = new Integer[r][r];  // 初始化备忘录
        for (int i = 0; i < r; i++) {
            triangle[i] = new int[i+1];
            for (int j = 0; j <= i; j++) {
                in.nextToken();
                triangle[i][j] = (int) in.nval;
            }
        }

        // 记忆化搜索
        int maxSum = dfs(0, 0, r);

        out.println(maxSum);
        out.flush();
        br.close();
        out.close();
    }

    public static int dfs(int i, int j, int r) {
        // 如果已经计算过，直接返回结果
        if (memo[i][j] != null) {
            return memo[i][j];
        }
        // 如果已经到达最后一行，返回当前值
        if (i == r - 1) {
            return memo[i][j] = triangle[i][j];
        }
        // 否则，返回从当前位置到底部的最大路径和
        return memo[i][j] = triangle[i][j] + Math.max(dfs(i + 1, j, r), dfs(i + 1, j + 1, r));
    }
}

记忆化搜索是一种优化技术，主要用于优化递归算法，避免重复计算相同的子问题。它的主要思路是将已经计算过的子问题的结果存储起来，当再次遇到相同的子问题时，直接从存储的结果中获取，而不是重新计算。

（2）动态规划

下面我们来看DP的解法：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(br);
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

    public static void main(String[] args) throws IOException {
    	// 读数据
        in.nextToken();
        int r = (int) in.nval;
        int[][] triangle = new int[r][];
        for (int i = 0; i < r; i++) {
            triangle[i] = new int[i+1];
            for (int j = 0; j <= i; j++) {
                in.nextToken();
                triangle[i][j] = (int) in.nval;
            }
        }

        // 动态规划
        int[][] dp = new int[r][r];
        dp[0][0] = triangle[0][0];
        for (int i = 1; i < r; i++) {
            for (int j = 0; j <= i; j++) {
                if (j == 0) {
                    dp[i][j] = dp[i-1][j] + triangle[i][j];
                } else if (j == i) {
                    dp[i][j] = dp[i-1][j-1] + triangle[i][j];
                } else {
                    dp[i][j] = Math.max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j];
                }
            }
        }

		// 筛选答案（找到最后一行每个位置的路径和最大值）
        int maxSum = dp[r-1][0];
        for (int i = 1; i < r; i++) {
            maxSum = Math.max(maxSum, dp[r-1][i]);
        }

        out.println(maxSum);
        out.flush();
        br.close();
        out.close();
    }
}

首先，我们定义状态 dp[i][j]，表示从金字塔顶部到第 i 行第 j 列的最大路径和。

这里，i 和 j 的范围都是从 0 开始的。

然后，我们需要找出状态转移方程（其实就是分析有多少种可能性）。

对于每一个位置 (i, j)，我们可以从其上方 (i-1, j) 或者左上方 (i-1, j-1) 移动过来。

因此，到达当前位置的路径和就是上方或者左上方的路径和加上当前位置的值，我们选择其中的最大值作为当前位置的路径和。

具体来说，状态转移方程可以写成如下形式：

当 j == 0（即在每一行的最左边）时，只能从上方移动过来，所以 dp[i][j] = dp[i-1][j] + triangle[i][j]。
当 j == i（即在每一行的最右边）时，只能从左上方移动过来，所以 dp[i][j] = dp[i-1][j-1] + triangle[i][j]。
当 0 < j < i 时，可以从上方或者左上方移动过来，所以 dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]。

最后，我们返回最后一行中的最大值，即为可能得到的最大的和。