【区块链】C语言编程实现三叉Merkle树

1. Merkle树简介

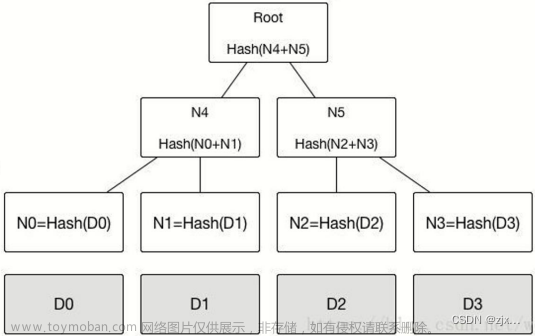
  如上图所示，Merkle 树的叶子节点为交易序列，对每一笔交易进行 Hash（SHA 256算法） 之后，然后对得到的 Hash 节点进行拼接再次进行 Hash 运算，如此递归直到递归至根节点。

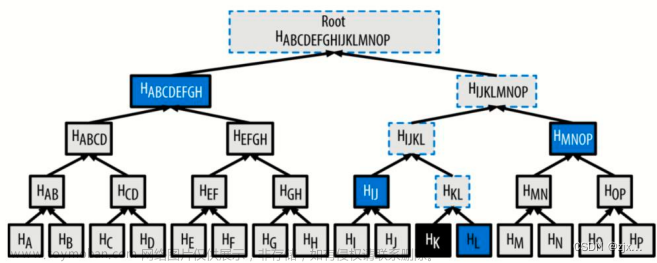
  如上图所示 Merkle 树的优点在于可快速验证某个区块是否存在指定交易，如要验证 $H_k$是否存在于该区块中，只要将 $H_L、H_{IJ}、H_{MNOP}、H_{ABCDEFG}$节点得到，然后从下到上不断 Hash，最后与根节点的 Hash 值进行比较，就可以快速判断交易是否在该区块中。

2. 构建Merkle树

1. 头文件及Merkle节点类型

# include <iostream>
# include <functional>
# include<string>
using namespace std;
typedef struct MerkleNode {
	MerkleNode* Left;
	MerkleNode* Middle;
	MerkleNode* Right;
	MerkleNode* parent;
	size_t data;
};
struct MerkleTree {
	MerkleNode* RootNode;
}root;

2. 创建三叉merkle所需函数

/* 创建merkle树 */
MerkleNode* queue[100000];
int front = 0, rear = 0, new_rear = 0;
int n;
// 字符串加密
size_t encrypt(string strInput)
{
	hash<string> Hash;
	size_t hashVal = Hash(strInput);
	return hashVal;
}

// size_t转换为字符串
string type_convert(size_t input)
{
	string output = to_string(input);
	return output;
}

// 字符串拼接
string concat(string one, string two,string three)
{
	string output = one + two + three;
	return output;
}

// 初始化叶子节点
void init_leaf_node(MerkleNode*& node,size_t data)
{
	node = (MerkleNode*)malloc(sizeof(MerkleNode));
	node->data = encrypt(type_convert(data));
	node->Left = NULL;
	node->Middle = NULL;
	node->Right = NULL;
}

// 对最后一个节点进行拷贝
MerkleNode* copy_node(MerkleNode* node)
{
	MerkleNode* new_node = (MerkleNode*)malloc(sizeof(MerkleNode));
	new_node->Left = NULL;
	new_node->Middle = NULL;
	new_node->Right = NULL;
	new_node->data = node->data;
	return new_node;
}

// 初始化分枝节点
void init_branch_node(MerkleNode* Left, MerkleNode* Middle, MerkleNode* Right)
{
	MerkleNode* node = (MerkleNode*)malloc(sizeof(MerkleNode));
	node->Left = Left;
	node->Middle = Middle;
	node->Right = Right;
	Left->parent = node;
	Middle->parent = node;
	Right->parent = node;
	node->data = encrypt(concat(type_convert(Left->data), type_convert(Middle->data), type_convert(Right->data)));
	queue[new_rear++] = node;
}

// 根据队列中的节点生成其父节点
void create_new_layer()
{
	// 补足剩余节点
	int remainder = rear % 3;
	int res = 0;
	if (remainder != 0)
	{
		res = 3 - remainder;
		MerkleNode* node = queue[rear - 1];
		for (int i = 0; i < res; i++)
		{
			queue[rear++] = copy_node(node);
		}
	}

	int loop = (rear + res) / 3;


	for (int i = 0; i < loop; i++)
	{
		MerkleNode* Left = queue[front++];
		MerkleNode* Middle = queue[front++];
		MerkleNode* Right = queue[front++];
		init_branch_node(Left, Middle, Right);
	}
	rear = new_rear;
	new_rear = 0;
	front = 0;
}

// 创建merkle树
void create_merkle_tree(MerkleTree*& root)
{
	while (rear != 1)
	{
		create_new_layer();
	}
	root = (MerkleTree*)malloc(sizeof(MerkleTree));
	root->RootNode = queue[rear-1];
	root->RootNode->parent = NULL;
}

// 输入数据
void init_data()
{
	cout << "请输入交易序列个数：";
	cin >> n;
	cout << "请输入每一笔交易（中间以空格隔开）：";
	for (int i = 0; i < n; i++)
	{
		MerkleNode* node;
		size_t data;
		cin >> data;
		init_leaf_node(node, data);
		queue[rear++] = node;
	}
}

3. 生成SPV路径

SPV路径生成代码：

/*  生成SPV路径  */ 
size_t spv_queue[100010];
MerkleNode *sequence[100010];
int seq_front = 0, seq_rear = 0;
int spv_front = 0,spv_rear = 0;
int spv_flag[100010], flag_idx = 0;

void init_all_node_sequence(MerkleNode* node)
{
	sequence[++seq_rear] = node;
	while (seq_front != seq_rear)
	{
		MerkleNode* new_node = sequence[++seq_front];
		if (new_node->Left != NULL)
		{
			sequence[++seq_rear] = new_node->Left;
		}
		if (new_node->Middle != NULL)
		{
			sequence[++seq_rear] = new_node->Middle;
		}
		if (new_node->Right != NULL)
		{
			sequence[++seq_rear] = new_node->Right;
		}
	}
	seq_front = 0;
}

void init_spv_path(int idx,MerkleTree *root)
{
	MerkleNode* head_node = root->RootNode;
	init_all_node_sequence(head_node);

	int cnt;
	if (n % 3 == 0)
	{
		cnt = 3;
	}
	else if((n + 1) % 3 == 0) {
		cnt = n + 1;
	}
	else {
		cnt = n + 2;
	}
	int seq_idx = seq_rear - (cnt - idx);
	cout << "该交易的哈希值为：" << sequence[seq_idx]->data<< endl;

	MerkleNode* node = sequence[seq_idx];

	while (node->parent)
	{
		MerkleNode* parent = node->parent;
		if (node == parent->Left)
		{
			spv_flag[flag_idx++] = 0;
			spv_queue[++spv_rear] = parent->Middle->data;
			spv_queue[++spv_rear] = parent->Right->data;
		}
		else if (node == parent->Middle)
		{
			spv_flag[flag_idx++] = 1;
			spv_queue[++spv_rear] = parent->Left->data;
			spv_queue[++spv_rear] = parent->Right->data;
		}
		else {
			spv_flag[flag_idx++] = 2;
			spv_queue[++spv_rear] = parent->Left->data;
			spv_queue[++spv_rear] = parent->Middle->data;
		}
		node = node->parent;
	}

}

void print_spv_path(int idx)
{
	cout << "交易序列号" << idx << "的SPV路径为：";
	while (spv_front != spv_rear)
	{
		cout << spv_queue[++spv_front] << " ";
	}
	cout << endl;
	spv_front = 0;
	cout << "生成交易在其兄弟节点中的位置序列为（0为Left，1为Middle，2为Right）：";
	for (int i = 0; i < flag_idx; i++)
	{
		cout << spv_flag[i] << " ";
	}
}

4. 验证SPV路径

SPV路径验证代码：

/* 验证SPV路径 */
size_t root_hash, spv_path[1010], hash_val;
int spv_length;
void judge_spv_path()
{
	cout << "请输入merkle树根节点哈希值：";
	cin >> root_hash;

	cout << "请输入SPV路径长度：";
	cin >> spv_length;
	cout << "请输入SPV路径（中间用空格隔开）：";
	for (int i = 0; i < spv_length; i++)
	{
		cin >> spv_path[i];
	}

	int pos_cnt, pos_sqe[100010];
	cout << "请输入交易位置序列个数：";
	cin >> pos_cnt;
	cout << "请输入交易位置序列（中间用空格隔开）：";
	for (int i = 0; i < pos_cnt; i++)
	{
		cin >> pos_sqe[i];
	}

	cout << "请输入要查询的交易哈希值：";
	cin >> hash_val;

	int path_idx = 0, pos_idx = 0;
	while (path_idx != spv_length)
	{
		size_t one = spv_path[path_idx++];
		size_t two = spv_path[path_idx++];
		if (pos_sqe[pos_idx] == 0)
		{
			hash_val = encrypt(concat(type_convert(hash_val), type_convert(one), type_convert(two)));
		}
		else if (pos_sqe[pos_idx] == 1)
		{
			hash_val = encrypt(concat(type_convert(one), type_convert(hash_val), type_convert(two)));
		}
		else {
			hash_val = encrypt(concat(type_convert(one), type_convert(two), type_convert(hash_val)));
		}
		pos_idx++;
	}
	cout << "SPV计算得到的哈希值为：" << hash_val <<endl;
	cout << "头节点哈希值为：" << root_hash << endl;
	if (hash_val == root_hash)
	{
		cout << "SPV路径验证成功！！！" << endl << endl << endl;
	}
}

5. 三叉Merkle树创建、SPV生成及验证总程序

# define _CRT_SECURE_NO_DEPRECATE
# include <iostream>
# include <functional>
# include<string>
using namespace std;
typedef struct MerkleNode {
	MerkleNode* Left;
	MerkleNode* Middle;
	MerkleNode* Right;
	MerkleNode* parent;
	size_t data;
};
struct MerkleTree {
	MerkleNode* RootNode;
}root;

/* 创建merkle树 */
MerkleNode* queue[100000];
int front = 0, rear = 0, new_rear = 0;
int n;
// 字符串加密
size_t encrypt(string strInput)
{
	hash<string> Hash;
	size_t hashVal = Hash(strInput);
	return hashVal;
}

// size_t转换为字符串
string type_convert(size_t input)
{
	string output = to_string(input);
	return output;
}

// 字符串拼接
string concat(string one, string two,string three)
{
	string output = one + two + three;
	return output;
}

// 初始化叶子节点
void init_leaf_node(MerkleNode*& node,size_t data)
{
	node = (MerkleNode*)malloc(sizeof(MerkleNode));
	node->data = encrypt(type_convert(data));
	node->Left = NULL;
	node->Middle = NULL;
	node->Right = NULL;
}

// 对最后一个节点进行拷贝
MerkleNode* copy_node(MerkleNode* node)
{
	MerkleNode* new_node = (MerkleNode*)malloc(sizeof(MerkleNode));
	new_node->Left = NULL;
	new_node->Middle = NULL;
	new_node->Right = NULL;
	new_node->data = node->data;
	return new_node;
}

// 初始化分枝节点
void init_branch_node(MerkleNode* Left, MerkleNode* Middle, MerkleNode* Right)
{
	MerkleNode* node = (MerkleNode*)malloc(sizeof(MerkleNode));
	node->Left = Left;
	node->Middle = Middle;
	node->Right = Right;
	Left->parent = node;
	Middle->parent = node;
	Right->parent = node;
	node->data = encrypt(concat(type_convert(Left->data), type_convert(Middle->data), type_convert(Right->data)));
	queue[new_rear++] = node;
}

// 根据队列中的节点生成其父节点
void create_new_layer()
{
	// 补足剩余节点
	int remainder = rear % 3;
	int res = 0;
	if (remainder != 0)
	{
		res = 3 - remainder;
		MerkleNode* node = queue[rear - 1];
		for (int i = 0; i < res; i++)
		{
			queue[rear++] = copy_node(node);
		}
	}

	int loop = (rear + res) / 3;


	for (int i = 0; i < loop; i++)
	{
		MerkleNode* Left = queue[front++];
		MerkleNode* Middle = queue[front++];
		MerkleNode* Right = queue[front++];
		init_branch_node(Left, Middle, Right);
	}
	rear = new_rear;
	new_rear = 0;
	front = 0;
}

// 创建merkle树
void create_merkle_tree(MerkleTree*& root)
{
	while (rear != 1)
	{
		create_new_layer();
	}
	root = (MerkleTree*)malloc(sizeof(MerkleTree));
	root->RootNode = queue[rear-1];
	root->RootNode->parent = NULL;
}

// 输入数据
void init_data()
{
	cout << "请输入交易序列个数：";
	cin >> n;
	cout << "请输入每一笔交易（中间以空格隔开）：";
	for (int i = 0; i < n; i++)
	{
		MerkleNode* node;
		size_t data;
		cin >> data;
		init_leaf_node(node, data);
		queue[rear++] = node;
	}
}



/*  生成SPV路径  */ 
size_t spv_queue[100010];
MerkleNode *sequence[100010];
int seq_front = 0, seq_rear = 0;
int spv_front = 0,spv_rear = 0;
int spv_flag[100010], flag_idx = 0;

void init_all_node_sequence(MerkleNode* node)
{
	sequence[++seq_rear] = node;
	while (seq_front != seq_rear)
	{
		MerkleNode* new_node = sequence[++seq_front];
		if (new_node->Left != NULL)
		{
			sequence[++seq_rear] = new_node->Left;
		}
		if (new_node->Middle != NULL)
		{
			sequence[++seq_rear] = new_node->Middle;
		}
		if (new_node->Right != NULL)
		{
			sequence[++seq_rear] = new_node->Right;
		}
	}
	seq_front = 0;
}

void init_spv_path(int idx,MerkleTree *root)
{
	MerkleNode* head_node = root->RootNode;
	init_all_node_sequence(head_node);

	int cnt;
	if (n % 3 == 0)
	{
		cnt = 3;
	}
	else if((n + 1) % 3 == 0) {
		cnt = n + 1;
	}
	else {
		cnt = n + 2;
	}
	int seq_idx = seq_rear - (cnt - idx);
	cout << "该交易的哈希值为：" << sequence[seq_idx]->data<< endl;

	MerkleNode* node = sequence[seq_idx];

	while (node->parent)
	{
		MerkleNode* parent = node->parent;
		if (node == parent->Left)
		{
			spv_flag[flag_idx++] = 0;
			spv_queue[++spv_rear] = parent->Middle->data;
			spv_queue[++spv_rear] = parent->Right->data;
		}
		else if (node == parent->Middle)
		{
			spv_flag[flag_idx++] = 1;
			spv_queue[++spv_rear] = parent->Left->data;
			spv_queue[++spv_rear] = parent->Right->data;
		}
		else {
			spv_flag[flag_idx++] = 2;
			spv_queue[++spv_rear] = parent->Left->data;
			spv_queue[++spv_rear] = parent->Middle->data;
		}
		node = node->parent;
	}

}

void print_spv_path(int idx)
{
	cout << "交易序列号" << idx << "的SPV路径为：";
	while (spv_front != spv_rear)
	{
		cout << spv_queue[++spv_front] << " ";
	}
	cout << endl;
	spv_front = 0;
	cout << "生成交易在其兄弟节点中的位置序列为（0为Left，1为Middle，2为Right）：";
	for (int i = 0; i < flag_idx; i++)
	{
		cout << spv_flag[i] << " ";
	}
}

/* 验证SPV路径 */
size_t root_hash, spv_path[1010], hash_val;
int spv_length;
void judge_spv_path()
{
	cout << "请输入merkle树根节点哈希值：";
	cin >> root_hash;

	cout << "请输入SPV路径长度：";
	cin >> spv_length;
	cout << "请输入SPV路径（中间用空格隔开）：";
	for (int i = 0; i < spv_length; i++)
	{
		cin >> spv_path[i];
	}

	int pos_cnt, pos_sqe[100010];
	cout << "请输入交易位置序列个数：";
	cin >> pos_cnt;
	cout << "请输入交易位置序列（中间用空格隔开）：";
	for (int i = 0; i < pos_cnt; i++)
	{
		cin >> pos_sqe[i];
	}

	cout << "请输入要查询的交易哈希值：";
	cin >> hash_val;

	int path_idx = 0, pos_idx = 0;
	while (path_idx != spv_length)
	{
		size_t one = spv_path[path_idx++];
		size_t two = spv_path[path_idx++];
		if (pos_sqe[pos_idx] == 0)
		{
			hash_val = encrypt(concat(type_convert(hash_val), type_convert(one), type_convert(two)));
		}
		else if (pos_sqe[pos_idx] == 1)
		{
			hash_val = encrypt(concat(type_convert(one), type_convert(hash_val), type_convert(two)));
		}
		else {
			hash_val = encrypt(concat(type_convert(one), type_convert(two), type_convert(hash_val)));
		}
		pos_idx++;
	}
	cout << "SPV计算得到的哈希值为：" << hash_val <<endl;
	cout << "头节点哈希值为：" << root_hash << endl;
	if (hash_val == root_hash)
	{
		cout << "SPV路径验证成功！！！" << endl << endl << endl;
	}
}



int main()
{

	cout << "================================================  Merkle树构建部分  ===================================================" << endl << endl;
	init_data();	// 数据初始化（输入相关数据）
	// 生成 Merkle 树
	MerkleTree* root;
	create_merkle_tree(root);
	cout << "merkle树根哈希值为：" << root->RootNode->data << endl;
	cout << "merkle树构建完成！" << endl << endl << endl;

	// 生成SPV路径
	cout << "================================================  SPV路径生成部分  ===================================================" << endl << endl;
	int idx;
	cout << "请输入交易序号（i）：";
	cin >> idx;
	init_spv_path(idx, root);
	print_spv_path(idx);
	cout << endl << endl << endl;

	// 验证SPV路径
	cout << "================================================  SPV路径验证部分  ===================================================" << endl << endl;
	judge_spv_path();

	return 0;
}

6. 程序运行结果

文章来源地址https://www.toymoban.com/news/detail-850560.html

到了这里，关于【区块链】C语言编程实现三叉Merkle树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！