1.背景介绍
深度学习是人工智能领域的一个重要分支,它主要通过模拟人类大脑中的神经网络来实现智能化的计算和决策。在深度学习中,矩阵内积是一种非常重要的数学操作,它在各种算法中都有着重要的应用。本文将深入探讨矩阵内积在深度学习中的潜在力量,并提供详细的解释和代码实例。
2.核心概念与联系
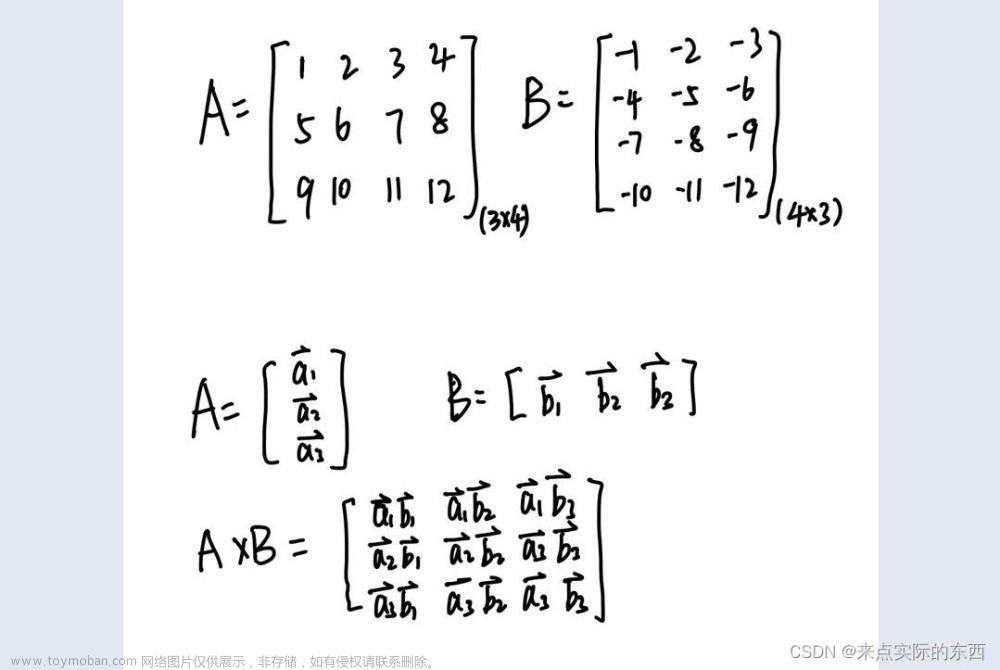
矩阵内积,也称为点积或者欧氏积,是两个向量在特定方向上的乘积。在深度学习中,矩阵内积主要用于计算向量之间的相似度、计算梯度、计算损失函数等。
在深度学习中,矩阵内积与以下核心概念密切相关:
- 线性代数:线性代数是深度学习的基础,矩阵内积是线性代数中的一个重要概念。
- 梯度下降:梯度下降是深度学习中最基本的优化算法,矩阵内积在计算梯度时有着重要作用。
- 损失函数:损失函数是深度学习模型的评估标准,矩阵内积在计算损失函数时有着重要作用。
- 正则化:正则化是防止过拟合的一种方法,矩阵内积在正则化中有着重要作用。
3.核心算法原理和具体操作步骤以及数学模型公式详细讲解
3.1 矩阵内积的定义与基本性质
矩阵内积是两个向量的乘积,定义如下:
$$ \mathbf{a} \cdot \mathbf{b} = \sum{i=1}^{n} ai b_i $$
其中,$\mathbf{a}$ 和 $\mathbf{b}$ 是 $n$ 维向量,$ai$ 和 $bi$ 是向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的第 $i$ 个元素。
矩阵内积具有以下基本性质:
- 交换律:$\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$
- 分配律:$\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}$
- 非负性:如果 $\mathbf{a}$ 和 $\mathbf{b}$ 都非负,则 $\mathbf{a} \cdot \mathbf{b}$ 也是非负的。
3.2 矩阵内积在梯度下降中的应用
梯度下降是深度学习中最基本的优化算法,其目标是最小化损失函数 $J(\mathbf{w})$。在梯度下降中,我们需要计算损失函数梯度 $\nabla J(\mathbf{w})$,然后更新权重 $\mathbf{w}$。矩阵内积在计算梯度时有着重要作用。
假设损失函数 $J(\mathbf{w})$ 的梯度可以表示为:
$$ \nabla J(\mathbf{w}) = \mathbf{g} \cdot \mathbf{w} $$
其中,$\mathbf{g}$ 是一个 $m$ 维向量,表示损失函数梯度的方向。在梯度下降中,我们需要更新权重 $\mathbf{w}$:
$$ \mathbf{w} \leftarrow \mathbf{w} - \eta \nabla J(\mathbf{w}) = \mathbf{w} - \eta (\mathbf{g} \cdot \mathbf{w}) $$
其中,$\eta$ 是学习率。
3.3 矩阵内积在损失函数中的应用
损失函数是深度学习模型的评估标准,常常是一个矩阵内积形式。例如,在线性回归中,损失函数可以表示为:
$$ J(\mathbf{w}) = \frac{1}{2} \|\mathbf{y} - \mathbf{X} \mathbf{w}\|^2 $$
其中,$\mathbf{y}$ 是目标向量,$\mathbf{X}$ 是特征矩阵,$\mathbf{w}$ 是权重向量。可以将损失函数简化为:
$$ J(\mathbf{w}) = \frac{1}{2} (\mathbf{y} - \mathbf{X} \mathbf{w}) \cdot (\mathbf{y} - \mathbf{X} \mathbf{w}) $$
3.4 矩阵内积在正则化中的应用
正则化是防止过拟合的一种方法,常常通过添加一个正则项到损失函数中实现。矩阵内积在正则化中有着重要作用。例如,在L2正则化中,正则项可以表示为:
$$ R(\mathbf{w}) = \frac{1}{2} \|\mathbf{w}\|^2 $$
将正则项添加到损失函数中,得到的总损失函数为:
$$ J(\mathbf{w}) = \frac{1}{2} \|\mathbf{y} - \mathbf{X} \mathbf{w}\|^2 + \frac{\lambda}{2} \|\mathbf{w}\|^2 $$
其中,$\lambda$ 是正则化强度。
4.具体代码实例和详细解释说明
在本节中,我们将通过一个简单的线性回归示例来展示矩阵内积在深度学习中的应用。
4.1 数据准备
首先,我们需要准备一些数据。假设我们有一组线性回归问题的数据,其中 $x$ 是特征向量,$y$ 是目标向量。
```python import numpy as np
x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 4, 6, 8, 10]) ```
4.2 初始化权重向量
接下来,我们需要初始化权重向量 $\mathbf{w}$。假设我们已经初始化了权重向量。
python w = np.array([0])
4.3 计算损失函数
现在,我们可以计算损失函数。在线性回归中,损失函数是一个矩阵内积形式。
```python def loss(y, x, w): yhat = x @ w return 0.5 * np.sum((y - yhat) ** 2)
lossvalue = loss(y, x, w) print("Loss:", lossvalue) ```
4.4 梯度下降更新权重
接下来,我们需要使用梯度下降算法更新权重。在线性回归中,梯度是一个矩阵内积形式。
```python def gradient(y, x, w): return x.T @ (y - x @ w)
grad = gradient(y, x, w) w -= 0.01 * grad ```
4.5 迭代更新权重
我们可以通过迭代更新权重来优化模型。以下是一个简单的迭代梯度下降示例。
python for i in range(1000): grad = gradient(y, x, w) w -= 0.01 * grad loss_value = loss(y, x, w) if i % 100 == 0: print("Iteration:", i, "Loss:", loss_value)
5.未来发展趋势与挑战
矩阵内积在深度学习中的应用非常广泛,未来仍有许多潜在的发展趋势和挑战。
- 高效的矩阵内积算法:随着数据规模的增加,计算矩阵内积的效率成为关键问题。未来可能会出现新的高效算法,提高矩阵内积计算的速度。
- 矩阵内积在新算法中的应用:未来,矩阵内积可能会被应用到新的深度学习算法中,为深度学习带来更多的创新。
- 矩阵内积在硬件加速中的应用:随着人工智能硬件的发展,如GPU、TPU等,矩阵内积算法可能会在硬件加速中得到应用,提高深度学习模型的训练速度和效率。
6.附录常见问题与解答
Q1. 矩阵内积与向量积的区别是什么? A1. 矩阵内积是两个向量的乘积,而向量积是一个向量在特定方向上的乘积。矩阵内积需要两个向量,而向量积只需要一个向量。
Q2. 矩阵内积与点积的区别是什么? A2. 矩阵内积是两个向量的乘积,而点积是两个向量的乘积。矩阵内积需要两个向量,而点积只需要一个向量。
Q3. 矩阵内积在深度学习中的应用有哪些? A3. 矩阵内积在深度学习中的应用包括线性代数、梯度下降、损失函数计算、正则化等。
Q4. 如何计算矩阵内积? A4. 矩阵内积可以通过元素乘积的和来计算。例如,对于两个向量 $\mathbf{a}$ 和 $\mathbf{b}$,矩阵内积可以表示为:文章来源:https://www.toymoban.com/news/detail-850748.html
$$ \mathbf{a} \cdot \mathbf{b} = a1 b1 + a2 b2 + \cdots + an bn $$文章来源地址https://www.toymoban.com/news/detail-850748.html
到了这里,关于矩阵内积在深度学习中的潜在力量的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!