动态规划:背包问题-暗黑（买装备）-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划:背包问题-暗黑（买装备）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

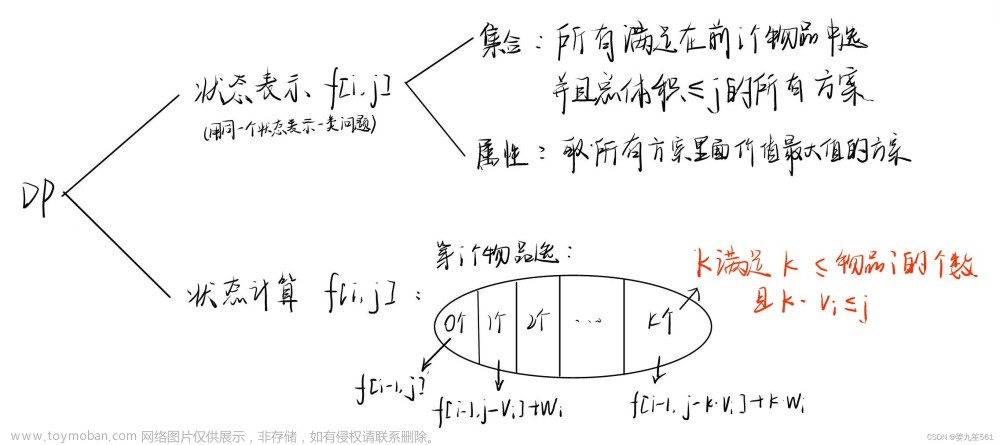
题目内容

暗黑游戏中，装备直接决定玩家人物的能力。可以使用Pg和Rune购买需要的物品。暗黑市场中的装备，每件有不同的价格（Pg和Rune）、能力值、最大可购买件数。Kid作为暗黑战网的一个玩家，当然希望使用尽可能少的Pg和Rune购买更优的装备，以获得最高的能力值。请你帮忙计算出现有支付能力下的最大可以获得的能力值。

输入

第一行，三个整数 $N$ , $P$ , $R$ ,分别代表市场中物品种类，Pg的支付能力和Rune的支付能力。第 $2... N + 1$ 行，每行四个整数，前两个整数分别为购买此物品需要花费的Pg，Rune，第三个整数若为 $0$ ，则说明此物品可以购买无数件，若为其他数字，则为此物品可购买的最多件数( $S$ )，第四个整数为该装备的能力值。

输出

仅一行,一个整数，最大可获得的能力值

题解

一道DP题，可以使用二进制优化。具体什么是二进制优化。就是任意一个数丢可以表示为 $m$ 个 $2^n$ 相加，比如 $7 = 2^0 + 2 ^ 1 + 2 ^ 2$
这样优化后，复杂度仅需 $\sum items_i)$ 文章来源地址https://www.toymoban.com/news/detail-851021.html

实现

#include <iostream>
#include <vector>
using namespace std;

struct item {
	int p, r, w;
};//记录Pg价格，Rune价格以及价值
vector<item> items;//结构体vector
int n, P, R;
int dp[210][210];

int main() {
	cin >> n >> P >> R;
	int a, b, c, d;
	for (int i = 1; i <= n; i++) {
		cin >> a >> b >> c >> d;
		if (c == 0) c = min(P / a, R / b);//能买几件
		for (int j = 1; j <= c; j *= 2) {//二进制拆分
			c -= j;
			item tmp;
			tmp.p = a * j;
			tmp.r = b * j;
			tmp.w = d * j;
			items.push_back(tmp);//放入数组
		}
		if (c) {//若还有剩余
			item tmp;
			tmp.p = a * c;
			tmp.r = b * c;
			tmp.w = d * c;
			items.push_back(tmp);
		}
	}
	//正常dp
	for (int i = 0; i < items.size(); i++) {
		for (int j = P; j >= items[i].p; j--) {
			for (int k = R; k >= items[i].r; k--) {//注意逆序
				if (j >= items[i].p && k >= items[i].r) {
					dp[j][k] = max(dp[j][k], dp[j - items[i].p][k - items[i].r] + items[i].w);
				}
			}
		}
	}
	cout << dp[P][R];//输出
	return 0;
}