1. Toy模板网首页
  2. > Toy博客

C++进阶--哈希

7月前 作者：诡异森林。 分类：Toy博客 阅读(26) 违法举报

这篇具有很好参考价值的文章主要介绍了C++进阶--哈希。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

哈希概念

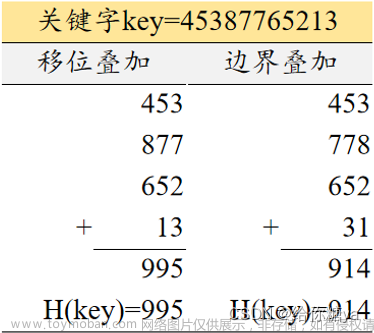
哈希（Hash）是一种常见的密码学技术和数据结构，它将任意长度的输入通过散列算法转换成固定长度的输出，这个输出被称为散列值或哈希值。哈希函数是一种单向函数，即从哈希值无法反推出原始输入值。

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
哈希函数具有以下特点：

  1. 唯一性：相同的输入一定会得到相同的输出，保证了相同数据的哈希值是唯一的。
  2. 固定长度：不论输入的长度是多少，哈希函数都能生成固定长度的哈希值。
  3. 高效性：哈希函数计算速度快，适用于大规模数据的处理。
  4. 不可逆性：从哈希值无法推导出输入的原始数据，即使输入数据的微小变化也会导致输出值的巨大变化，保证了数据的安全性和完整性。

哈希冲突

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
哈希冲突是指在使用哈希函数将数据映射到哈希表存储时，可能会出现两个或多个不同的键被映射到相同的哈希值的情况。由于哈希表的存储空间是有限的，而要存储的数据量可能很大，所以哈希冲突是不可避免的。

哈希冲突可能会导致以下问题：

  1. 数据丢失：当两个键被映射到相同的哈希值时，只能存储其中一个键，另一个键的数据可能会丢失。
  2. 性能下降：哈希冲突会导致在查找、插入和删除操作时需要进行额外的处理，从而降低了哈希表的性能。

哈希冲突的解决

为了解决哈希冲突，常见的方法有以下四种：

  1. 开放定址法：在遇到哈希冲突时，寻找一个新的空闲的哈希地址来存储冲突的元素。常见的开放定址法包括线性探测法、二次探测法和双重散列法等。
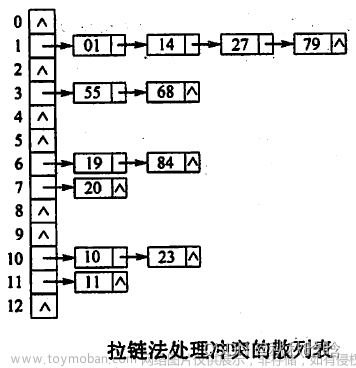
  2. 链地址法（拉链法）：将哈希表的每个槽（桶）设为链表头节点，每个链表存储哈希值相同的元素。当发生哈希冲突时，冲突的元素会被添加到对应槽的链表中。

开放地址法

线性探测和删除问题

线性探测：当插入一个键值对时，如果发生哈希冲突，线性探测会尝试在哈希表中找到下一个可用的位置来存储冲突的数据。
.
具体而言，线性探测的步骤如下：

  1. 当发生哈希冲突时，计算下一个位置，通常使用线性递增的方式，即当前位置加上一个固定的增量。
  2. 如果下一个位置为空闲（没有被占用），则将冲突的数据存储在该位置。
  3. 如果下一个位置仍然被占用，继续计算下一个位置，直到找到空闲位置或遍历整个哈希表。

删除问题：如果对于一个key值进行删除，直接表示位置为空；那么会对相同哈希值的key值产生影响。
如上面的5与25；通过我们的线性探测：

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
这样不符合我们的想法；所以这里还需要通过标记的方法，对删除过的key不能直接标记为空；

代码

template<class K>
struct Hashfunc
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};
//特化
template<>
struct Hashfunc<string>
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (auto a : s)
		{
			hash += a;
			hash *= 31;
		}
		return hash;
	}
};

namespace open_address
{
	enum State
	{
		EMPTY,
		EXIST,
		DELETE
	};

	template<class K, class V>
	struct HashData
	{
		pair<K, V> _data;
		State _state = EMPTY;
	};

	
	template<class K, class V, class Hash = Hashfunc<K>>
	class HashTable
	{
	public:
		HashTable(size_t size = 10)
		{
			_tables.resize(size);
		}
		HashData<K, V>* Find(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();
			while (_tables[hashi]._state != EMPTY)
			{
				if (key == _tables[hashi]._data.first && _tables[hashi]._state == EXIST)
				{
					return &_tables[hashi];
				}
				hashi++;
				hashi %= _tables.size();
			}
			return nullptr;
		}
		bool Insert(const pair<K, V>& data)
		{
			//保证不能有相同的元素
			if (Find(data.first))
				return false;
			//扩容
			if (_n * 10 / _tables.size() >= 7)
			{
				HashTable<K, V> newHT(_tables.size() * 2);
				for (auto& a : _tables)
				{
					if (a._state == EXIST)
					{
						newHT.Insert(a._data);
					}
				}
				_tables.swap(newHT._tables);
			}
			Hash hs;
			//线性探测
			size_t hashi = hs(data.first) % _tables.size();
			while (_tables[hashi]._state == EXIST)
			{
				hashi++;
				hashi %= _tables.size();
			}

			_tables[hashi]._data = data;
			_tables[hashi]._state = EXIST;
			_n++;

			return true;
		}

		bool Erase(const K& key)
		{
			HashData<K, V>* ret = Find(key);
			if (ret)
			{
				_n--;
				ret->_state = DELETE;
				return true;
			}
			else
			{
				return false;
			}
		}
	private:
		vector<HashData<K, V>> _tables;
		size_t _n = 0; //实际存储的数据个数
	};

	void TestHT1()
	{
		int a[] = { 1,5,25,35,7,44,17,37 };
		HashTable<int, int> ht;
		//插入到哈希表
		for (auto e : a)
		{
			ht.Insert(make_pair(e, e));
		}
		//遍历和打印状态
		for (auto e : a)
		{
			auto ret = ht.Find(e);
			if (ret)
			{
				cout << ret->_data.first << ":Exist" << endl;
			}
			else
			{
				cout << ret->_data.first << ":Delete" << endl;
			}
		}
		cout << endl;

		ht.Erase(44);
		ht.Erase(25);
		for (auto e : a)
		{
			auto ret = ht.Find(e);
			if (ret)
			{
				cout << ret->_data.first << ":Exist" << endl;
			}
			else
			{
				cout << e << ":Delete" << endl;
			}
		}
		cout << endl;
	}

	struct Date
	{
		int _year;
		int _month;
		int _day;
	};

	struct HashFuncDate
	{
		size_t operator()(const Date& d)
		{
			size_t hash = 0;
			hash += d._year;
			hash *= 31;

			hash += d._month;
			hash *= 31;

			hash += d._day;
			hash *= 31;
			return hash;
		}
	};

	struct Person
	{
		string _name;
		string _id;
		string _tel;
		int _age;
		string _class;
		string _address;
	};
	struct HashFuncPerson
	{
		size_t operator()(const Person& p)
		{
			size_t hash = 0;
			for (auto e : p._id)
			{
				hash += e;
				hash *= 31;
			}
			return hash;
		}
	};
	void TestHT2()
	{
		HashTable<string, string> ht;
		ht.Insert(make_pair("length", "长度"));
		ht.Insert(make_pair("data", "数据"));

		HashTable<Person, int, HashFuncPerson> ht1;
		HashTable<Date, string, HashFuncDate> ht2;
	}
}

解释

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突

负载因子：负载因子（load factor）是指哈希表中已经存储的元素数量与哈希表容量之比。它可以用来衡量哈希表的填充程度。一般情况下，负载因子越高，表示哈希表中已经存储的元素越多，哈希冲突的概率可能会增加，因此需要进行扩容操作来降低冲突。
.
负载因子通常用一个小数来表示，例如0.75表示哈希表已经存储的元素数量占总容量的75%。负载因子的取值范围通常是0到1之间。
.
具体计算哈希表的负载因子可以根据实际情况来决定。一般来说，当负载因子超过一定阈值（如0.75），就需要考虑进行哈希表的扩容操作，以保持哈希表的性能和效率。
.
记住，哈希表的负载因子并非越高越好。过高的负载因子可能会导致哈希冲突增加，从而影响哈希表的效率；过低的负载因子可能会存在哈希的底层空间过大，插入的key值远低于底层空间大小，这样会浪费不必要的空间。因此，在设计哈希表时，需要根据实际情况选择合适的负载因子阈值，以平衡空间利用率和性能要求。

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突

测试1：
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
测试2：
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突

对于Date和Person：

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突

链地址法

代码

namespace hash_bucket
{
	template <class K,class V>
	struct HashNode
	{
		HashNode<K, V>* _next;
		pair<K, V> _kv;

		HashNode(const pair<K, V>& kv)
			:_next(nullptr),
			_kv(kv)
		{}
		
	};

	template<class K,class V,class Hash=Hashfunc<K>>
	class HashTable
	{
		typedef HashNode<K, V> Node;
	public:
		HashTable()
		{
			_tables.resize(10, nullptr);
			_n = 0;
		}

		~HashTable()
		{
			for (size_t i= 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		Node* Find(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}

				cur = cur->_next;
			}

			return nullptr;
		}

		bool Insert(const pair<K, V>& kv)
		{
			//查找是否有相同元素
			if (Find(kv.first))
				return false;

			Hash hs;
			//扩容
			if (_n == _tables.size())
			{
				vector<Node*> newTables(_tables.size() * 2, nullptr);
				for (size_t i = 0; i < _tables.size(); i++)
				{
					Node* cur = _tables[i];
					while (cur)
					{
						Node* next = cur->_next;

						size_t hashi = hs(cur->_kv.first) % newTables.size();
						cur->_next = newTables[hashi];
						newTables[hashi] = cur;

						cur = next;
					}
					_tables[i] = nullptr;
				}
				_tables.swap(newTables);
			}	

			size_t hashi = hs(kv.first) % _tables.size();
			Node* newnode = new Node(kv);

			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;

			++_n;
			return true;
		}

		bool Erase(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();
			Node* prev = nullptr;
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first==key)
				{
					if (prev)
					{
						prev->_next = cur->_next;
					}
					else
					{
						_tables[hashi] = cur->_next;
					}
					delete cur;
					_n--;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
			return false;
		}
		void Print()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					
					cout << "哈希值：" << i << "--" << "data:" << cur->_kv.first << endl;
					cur = cur->_next;
				}
			}
		}

		void Some()
		{
			size_t bucketSize = 0;//哈希桶数
			size_t maxBucketLen = 0;//最大哈希桶高度
			size_t sum = 0;//总数
			double averageBucketLen = 0;//哈希桶评价高度

			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				if (cur)
				{
					++bucketSize;
				}

				size_t bucketLen = 0;
				while (cur)
				{
					++bucketLen;
					cur = cur->_next;
				}

				sum += bucketLen;

				if (bucketLen > maxBucketLen)
				{
					maxBucketLen = bucketLen;
				}
			}

			averageBucketLen = (double)sum / (double)bucketSize;

			printf("load factor:%lf\n", (double)_n / _tables.size());//负载因子
			printf("哈希桶数:%d\n", _tables.size());
			printf("节点总数:%d\n", bucketSize);
			printf("最大哈希桶高度:%d\n", maxBucketLen);
			printf("平均哈希桶高度:%lf\n\n", averageBucketLen);
		}
	private:
		vector<Node*> _tables;
		size_t _n;
	};

	void TestHT1()
	{
		HashTable<int, int> ht;
		int a[] = { 1,4,24,34,7,44,17,37 };
		for (auto e : a)
		{
			ht.Insert(make_pair(e, e));
		}

		//插入测试打印
		ht.Print();
		cout << endl;
		//扩容后查看对应的哈希值
		ht.Insert(make_pair(5, 5));
		ht.Insert(make_pair(15, 15));
		ht.Insert(make_pair(25, 25));
		ht.Print();
		cout << endl;
		//删除测试
		ht.Erase(5);
		ht.Erase(15);
		ht.Erase(25);
		ht.Erase(35);

		ht.Print();
	}

	void TestHT2()
	{
		const size_t N = 100000;

		unordered_set<int> us;
		set<int> s;
		HashTable<int, int> ht;

		vector<int> v;
		v.reserve(N);
		srand(time(0));
		for (size_t i = 0; i < N; ++i)
		{
			//v.push_back(rand()); // N比较大时，重复值比较多
			//v.push_back(rand() + i); // 重复值相对少
			v.push_back(i); // 没有重复，有序
		}

		size_t begin1 = clock();
		for (auto e : v)
		{
			s.insert(e);
		}
		size_t end1 = clock();
		cout << "set insert:" << end1 - begin1 << endl;

		size_t begin2 = clock();
		for (auto e : v)
		{
			us.insert(e);
		}
		size_t end2 = clock();
		cout << "unordered_set insert:" << end2 - begin2 << endl;

		size_t begin10 = clock();
		for (auto e : v)
		{
			ht.Insert(make_pair(e, e));
		}
		size_t end10 = clock();
		cout << "HashTbale insert:" << end10 - begin10 << endl << endl;

		size_t begin3 = clock();
		for (auto e : v)
		{
			s.find(e);
		}
		size_t end3 = clock();
		cout << "set find:" << end3 - begin3 << endl;

		size_t begin4 = clock();
		for (auto e : v)
		{
			us.find(e);
		}
		size_t end4 = clock();
		cout << "unordered_set find:" << end4 - begin4 << endl;

		size_t begin11 = clock();
		for (auto e : v)
		{
			ht.Find(e);
		}
		size_t end11 = clock();
		cout << "HashTable find:" << end11 - begin11 << endl << endl;

		cout << "插入数据个数：" << us.size() << endl << endl;
		ht.Some();

		size_t begin5 = clock();
		for (auto e : v)
		{
			s.erase(e);
		}
		size_t end5 = clock();
		cout << "set erase:" << end5 - begin5 << endl;

		size_t begin6 = clock();
		for (auto e : v)
		{
			us.erase(e);
		}
		size_t end6 = clock();
		cout << "unordered_set erase:" << end6 - begin6 << endl;

		size_t begin12 = clock();
		for (auto e : v)
		{
			ht.Erase(e);
		}
		size_t end12 = clock();
		cout << "HashTable Erase:" << end12 - begin12 << endl << endl;
	}
}

解释

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
测试：
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突

性能测试

C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突
C++进阶--哈希,C++进阶,哈希算法,c++,散列表,哈希冲突文章来源地址https://www.toymoban.com/news/detail-851692.html

到了这里，关于C++进阶--哈希的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 查找算法【哈希表】 - 处理冲突的方法：开放地址法-线性探测法

    查找算法【哈希表】 - 处理冲突的方法：开放地址法-线性探测法

    查找算法【哈希表】 - 处理冲突的方法 无论如何设计散列函数，都 无法避免 发生冲突。 如果发生冲突，就需要处理冲突。 处理冲突的方法分为3种： 开放地址法 链地址法 建立公共溢出区。 【开放地址法】 开放地址法是线性存储空间上的解决方案，也被称为闭散列。 当发

    2024年02月12日
    浏览(39)
  • 哈希表/散列表(HashTable)c++实现

    哈希表/散列表(HashTable)c++实现

    目录 哈希表实现的思想 除留余数法  哈希冲突 第一种方法：探测法实现哈希表 探测法的思想  结点类  插入数据(insert) 冲突因子 数据扩容 哈希值  插入的代码实现以及哈希类 查找数据(find) 删除数据(erase) 第二种方法：拉链法实现哈希表 结点类 哈希类的成员 插入(insert)

    2024年02月10日
    浏览(45)
  • 【数据结构（C++版）】哈希表（散列表）

    【数据结构（C++版）】哈希表（散列表）

    目录   1. 散列表的概念 2. 散列函数的构造方法 2.1 直接定址法 2.2 除留余数法 2.3 数字分析法 2.4 平方取中法 3. 处理冲突的方法 3.1 开放定址法 3.1.1 线性探测法 3.1.2 平方探测法 3.1.3 双散列法 3.1.4 伪随机序列法 3.2 拉链法（链接法） 4. 散列查找及性能分析 5. 哈希的应用 5.1 位

    2024年02月15日
    浏览(46)
  • 【C++进阶07】哈希表and哈希桶

    【C++进阶07】哈希表and哈希桶

    顺序结构以及平衡树中 元素关键码与存储位置没有对应关系 因此查找一个元素 必须经过关键码的多次比较 顺序查找时间复杂度为O(N) 平衡树中为树的高度，即O( l o g 2 N log_2 N l o g 2 ​ N ) 搜索效率 = 搜索过程中元素的比较次数 理想的搜索方法：不经任何比较 一次直接从表中

    2024年01月23日
    浏览(38)
  • HELLO算法笔记之散列表（哈希）

    HELLO算法笔记之散列表（哈希）

    一、哈希表 建立键  key  与值  value  之间的映射，实现高效的元素查询。输入一个key，以O（1）获取对应的value 遍历： 知识点1、哈希函数： 将一个较大的输入空间映射到一个较小的输出空间。在哈希表中，输入空间是所有  key  ，输出空间是所有桶（数组索引）。换句话

    2024年02月10日
    浏览(37)
  • 数据结构算法设计——哈希表(散列表)

    数据结构算法设计——哈希表(散列表)

            哈希表 又叫 散列表 ，他们两个是同一个东西，本文全文采用“散列表”的叫法。散列表的本质其实就是一个 数组 ，他的作用就像使用数组时一样，输入下标可以得到对应元素，散列表可以实现 输入一个的时候得到这个的地址信息 。 下面是百科给出

    2024年02月03日
    浏览(60)
  • 【C++进阶】九、哈希表

    【C++进阶】九、哈希表

    目录 一、哈希概念 二、哈希冲突 三、哈希函数 四、哈希冲突解决 4.1 闭散列（开放定址法） 4.1.1 线性探测 4.1.2 二次探测 4.1.3 研究表明 五、哈希表的闭散列实现 5.1 闭散列哈希表的结构 5.2 闭散列的插入 5.2 闭散列的查找 5.3 闭散列的查找 5.4 哈希表取模问题 5.5 string类型无

    2024年02月09日
    浏览(41)
  • C++进阶--哈希

    C++进阶--哈希

    哈希（Hash）是一种常见的密码学技术和数据结构， 它将任意长度的输入通过散列算法转换成固定长度的输出，这个输出被称为散列值或哈希值 。 哈希函数是一种单向函数，即从哈希值无法反推出原始输入值 。 哈希函数具有以下特点 ： 唯一性 ：相同的输入一定会得到相同

    2024年04月15日
    浏览(26)
  • 查找算法【哈希表】 - 处理冲突的方法：开放地址法-二次探测法 & 随机探测法 & 再散列法

    查找算法【哈希表】 - 处理冲突的方法：开放地址法-二次探测法 & 随机探测法 & 再散列法

    查找算法【哈希表】 - 处理冲突的方法：开放地址法-二次探测法 随机探测法 再散列法 【二次探测法】 二次探测法指采用前后跳跃式探测的方法，发生冲突时，向后1位探测，向前1位探测，向后2^2 位探测，向前2^2 位探测……以跳跃式探测，避免堆积。 二次探测的增量序列为

    2024年02月10日
    浏览(42)
  • 【C++进阶】哈希（万字详解）—— 学习篇(上）

    【C++进阶】哈希（万字详解）—— 学习篇(上）

    🎇C++学习历程：入门 博客主页： 一起去看日落吗 持续分享博主的C++学习历程 博主的能力有限，出现错误希望大家不吝赐教 分享给大家一句我很喜欢的话： 也许你现在做的事情，暂时看不到成果，但不要忘记，树🌿成长之前也要扎根，也要在漫长的时光🌞中沉淀养分。静

    2024年02月02日
    浏览(34)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包