线性代数中的矩阵分解与稀疏处理-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性代数中的矩阵分解与稀疏处理。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.背景介绍

线性代数是计算机科学、数学、物理等多个领域的基础知识之一，其中矩阵分解和稀疏处理是线性代数中非常重要的两个方面。矩阵分解是指将一个矩阵分解为多个较小的矩阵的过程，这有助于我们更好地理解和解决问题。稀疏处理是指处理那些主要由零组成的矩阵的方法，这类矩阵在实际应用中非常常见，例如文本、图像、信号处理等领域。

在本文中，我们将深入探讨线性代数中的矩阵分解与稀疏处理，涵盖其核心概念、算法原理、具体操作步骤以及数学模型公式。此外，我们还将通过具体的代码实例来进行详细解释，并讨论未来发展趋势与挑战。

2.核心概念与联系

2.1矩阵分解

矩阵分解是指将一个矩阵分解为多个较小的矩阵的过程。这有助于我们更好地理解和解决问题。矩阵分解的主要方法有以下几种：

奇异值分解(Singular Value Decomposition, SVD)：将一个矩阵分解为三个矩阵的乘积。
特征分解(Eigenvalue Decomposition, EVD)：将一个正定矩阵分解为一个特征向量和特征值的乘积。
高斯消元法(Gaussian Elimination)：将一个矩阵通过消元操作转换为上三角矩阵或下三角矩阵。

2.2稀疏矩阵

稀疏矩阵是指主要由零组成的矩阵，其非零元素较少。稀疏矩阵在实际应用中非常常见，例如文本、图像、信号处理等领域。处理稀疏矩阵的主要方法有以下几种：

稀疏表示：将稀疏矩阵存储为仅保存非零元素的数据结构，以节省存储空间。
稀疏运算：针对稀疏矩阵进行优化的运算算法，以提高计算效率。
稀疏模型：将问题模型化简为稀疏矩阵的形式，以便更高效地解决问题。

3.核心算法原理和具体操作步骤以及数学模型公式详细讲解

3.1奇异值分解(SVD)

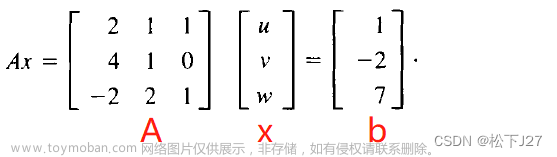
奇异值分解是一种矩阵分解方法，将一个矩阵分解为三个矩阵的乘积。给定一个矩阵A，其维度为m×n，SVD的过程如下：

计算A的奇异值矩阵S，其维度为n×n，其中S的对角线元素为奇异值。
计算两个矩阵U和V，其中U的维度为m×n，V的维度为n×n，且U和V的转置乘积为S。

SVD的数学模型公式为：

$$ A = U \Sigma V^T $$

其中，U是左奇异向量矩阵，Σ是奇异值矩阵，V是右奇异向量矩阵。

3.2特征分解(EVD)

特征分解是一种矩阵分解方法，将一个正定矩阵分解为一个特征向量和特征值的乘积。给定一个正定矩阵A，其维度为n×n，EVD的过程如下：

计算A的特征向量矩阵V，其维度为n×n，其中V的列为特征向量。
计算一个对角线矩阵Λ，其对角线元素为特征值。

EVD的数学模型公式为：

$$ A = V \Lambda V^T $$

其中，V是特征向量矩阵，Λ是特征值矩阵。

3.3高斯消元法

高斯消元法是一种矩阵分解方法，将一个矩阵通过消元操作转换为上三角矩阵或下三角矩阵。给定一个方阵A，其维度为n×n，高斯消元法的过程如下：

通过消元操作，将A转换为上三角矩阵U或下三角矩阵L。

高斯消元法的数学模型公式为：

$$ A = LU \quad 或 \quad A = UL $$

其中，L是下三角矩阵，U是上三角矩阵。

3.4稀疏矩阵存储

稀疏矩阵存储是一种稀疏矩阵的存储方法，将稀疏矩阵存储为仅保存非零元素的数据结构，以节省存储空间。给定一个稀疏矩阵A，其维度为m×n，稀疏矩阵存储的过程如下：

计算A的非零元素的行和列坐标，以及非零元素的值。
将非零元素的行和列坐标存储为两个一维数组，分别表示行和列坐标。
将非零元素的值存储为一个一维数组。

3.5稀疏矩阵运算

稀疏矩阵运算是针对稀疏矩阵进行优化的运算算法，以提高计算效率。给定两个稀疏矩阵A和B，其维度分别为m×n和n×p，稀疏矩阵运算的过程如下：

计算A和B的非零元素的行和列坐标，以及非零元素的值。
针对不同的运算类型(如加法、乘法等)，使用对应的稀疏矩阵运算算法，如Coo加法、Csr乘法等。
将运算结果的非零元素的行和列坐标和值存储为稀疏矩阵。

3.6稀疏模型

稀疏模型是将问题模型化简为稀疏矩阵的形式，以便更高效地解决问题。给定一个问题P，其稀疏模型的过程如下：

分析问题P，找出可以表示为稀疏矩阵的元素。
将问题P转换为稀疏矩阵表示。
针对稀疏矩阵表示的问题P，使用相应的稀疏矩阵算法进行解决。

4.具体代码实例和详细解释说明

4.1奇异值分解(SVD)

```python import numpy as np from scipy.linalg import svd

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) U, S, V = svd(A) print("U:\n", U) print("S:\n", S) print("V:\n", V) ```

在这个代码实例中，我们使用了scipy库中的svd函数来计算矩阵A的奇异值分解。U、S和V分别表示左奇异向量矩阵、奇异值矩阵和右奇异向量矩阵。

4.2特征分解(EVD)

```python import numpy as np from scipy.linalg import eig

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) V, L = eig(A) print("V:\n", V) print("L:\n", L) ```

在这个代码实例中，我们使用了scipy库中的eig函数来计算矩阵A的特征分解。V和L分别表示特征向量矩阵和特征值矩阵。

4.3高斯消元法

```python import numpy as np

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) L, U = np.linalg.lu(A) print("L:\n", L) print("U:\n", U) ```

在这个代码实例中，我们使用了numpy库中的linalg.lu函数来计算矩阵A的高斯消元法。L和U分别表示下三角矩阵和上三角矩阵。

4.4稀疏矩阵存储

```python from scipy.sparse import csr_matrix

data = np.array([1, 2, 3, 4, 5, 6]) row = np.array([0, 0, 1, 1, 2, 2]) col = np.array([0, 1, 0, 1, 0, 1])

A = csr_matrix((data, (row, col)), shape=(3, 2)) print(A) ```

在这个代码实例中，我们使用了scipy库中的csrmatrix函数来存储稀疏矩阵A。csrmatrix是一种稀疏矩阵存储方式，它使用了三个一维数组来存储行、列坐标和非零元素的值。

4.5稀疏矩阵运算

```python from scipy.sparse import csr_matrix

data1 = np.array([1, 2, 3, 4, 5, 6]) row1 = np.array([0, 0, 1, 1, 2, 2]) col1 = np.array([0, 1, 0, 1, 0, 1])

A1 = csr_matrix((data1, (row1, col1)), shape=(3, 2))

data2 = np.array([7, 8, 9, 10, 11, 12]) row2 = np.array([0, 1, 2, 2, 1, 2]) col2 = np.array([0, 0, 0, 1, 2, 2])

A2 = csr_matrix((data2, (row2, col2)), shape=(3, 2))

A3 = A1 + A2 print(A3) ```

在这个代码实例中，我们使用了scipy库中的csr_matrix函数来存储稀疏矩阵A1和A2，并使用了A1和A2的加法运算。A3是A1和A2的加法结果，也是一个稀疏矩阵。

4.6稀疏模型

```python

假设我们有一个线性回归问题，我们的目标是找到一个权重向量w，使得y = Xw最小

在这个问题中，X是一个高维稀疏矩阵，我们可以使用稀疏矩阵优化算法来解决这个问题

from scipy.sparse import csr_matrix import numpy as np

生成一个高维稀疏矩阵X

data = np.array([1, 2, 3, 4, 5, 6]) row = np.array([0, 0, 1, 1, 2, 2]) col = np.array([0, 1, 0, 1, 0, 1]) X = csr_matrix((data, (row, col)), shape=(1000, 100))

生成一个向量y

y = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

使用稀疏矩阵优化算法解决线性回归问题

这里我们使用了scipy库中的linalg.lstsq函数来计算最小二乘解

w = np.linalg.lstsq(X, y, rcond=None)[0] print("w:\n", w) ```

在这个代码实例中，我们假设我们有一个线性回归问题，我们的目标是找到一个权重向量w，使得y = Xw最小。在这个问题中，X是一个高维稀疏矩阵，我们可以使用稀疏矩阵优化算法来解决这个问题。我们使用了scipy库中的linalg.lstsq函数来计算最小二乘解。

5.未来发展趋势与挑战

未来的发展趋势和挑战包括：

随着数据规模的增加，如何更高效地处理和分析稀疏数据成为了一个重要的问题。
深度学习和机器学习的发展将加大对矩阵分解和稀疏处理的需求。
随着大数据技术的发展，如何在分布式环境中进行矩阵分解和稀疏处理成为了一个挑战。
如何在边缘计算和云计算环境中进行矩阵分解和稀疏处理成为了一个问题。

6.附录常见问题与解答

问题：什么是奇异值？答案：奇异值是矩阵奇异值分解的一个重要组成部分，它表示矩阵的“紧凑性”。奇异值越大，矩阵越稠密。
问题：什么是特征值？答案：特征值是矩阵特征分解的一个重要组成部分，它表示矩阵的“扩张性”。特征值越大，矩阵越可扩展。
问题：什么是高斯消元法？答案：高斯消元法是一种矩阵分解方法，它将一个矩阵通过消元操作转换为上三角矩阵或下三角矩阵。
问题：什么是稀疏矩阵？答案：稀疏矩阵是主要由零组成的矩阵，其非零元素较少。稀疏矩阵在实际应用中非常常见，例如文本、图像、信号处理等领域。
问题：如何存储稀疏矩阵？答答：稀疏矩阵可以使用多种存储方式，如Coo、Csr、Csc等。这些存储方式将稀疏矩阵存储为仅保存非零元素的数据结构，以节省存储空间。
问题：如何优化稀疏矩阵运算？答案：针对稀疏矩阵进行优化的运算算法，如Coo加法、Csr乘法等，可以提高计算效率。此外，在分布式和边缘计算环境中进行稀疏矩阵运算也是一种优化方法。
问题：如何解决线性回归问题中的稀疏矩阵？答案：可以使用稀疏矩阵优化算法来解决线性回归问题。例如，在这个博客中，我们使用了scipy库中的linalg.lstsq函数来计算最小二乘解。文章来源地址https://www.toymoban.com/news/detail-851899.html