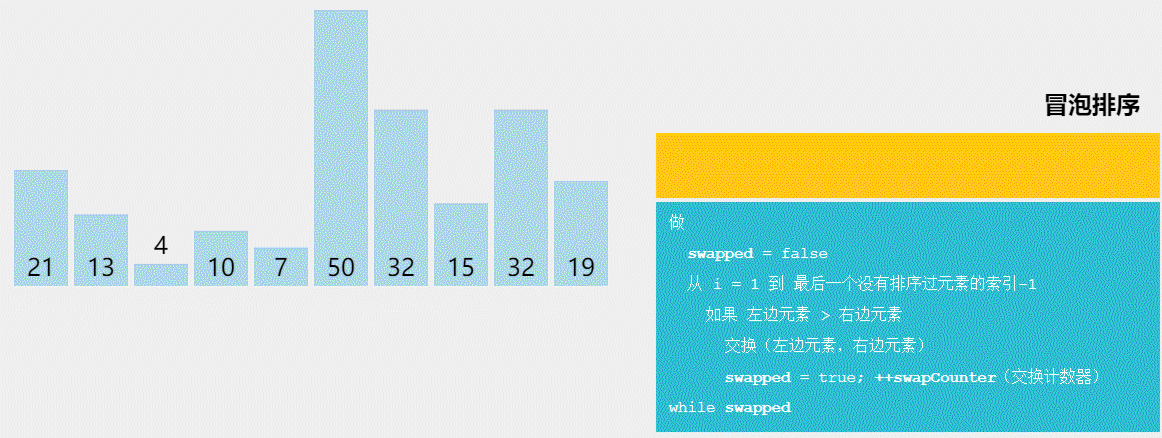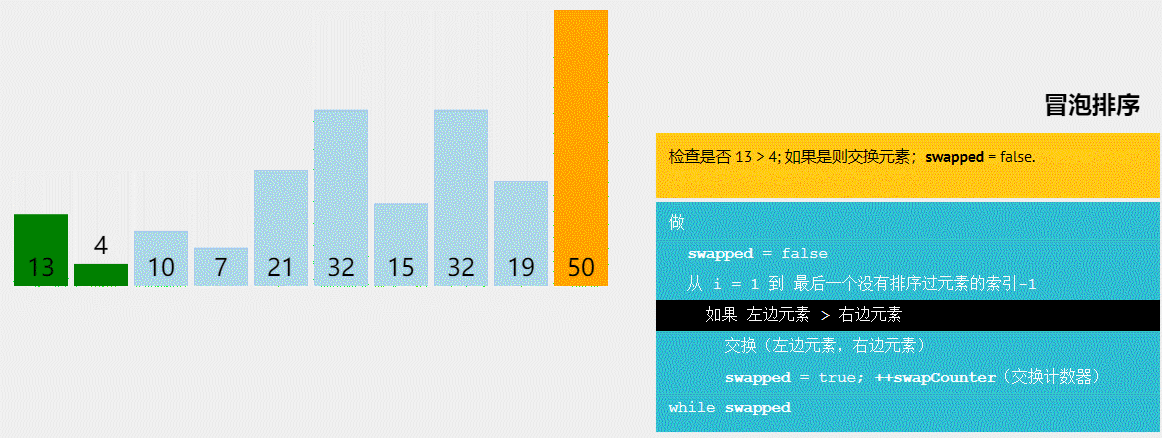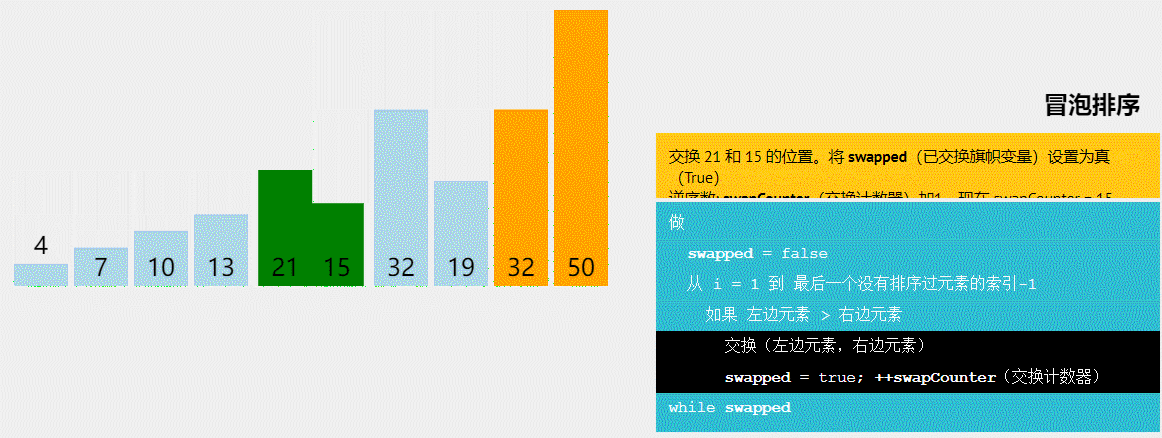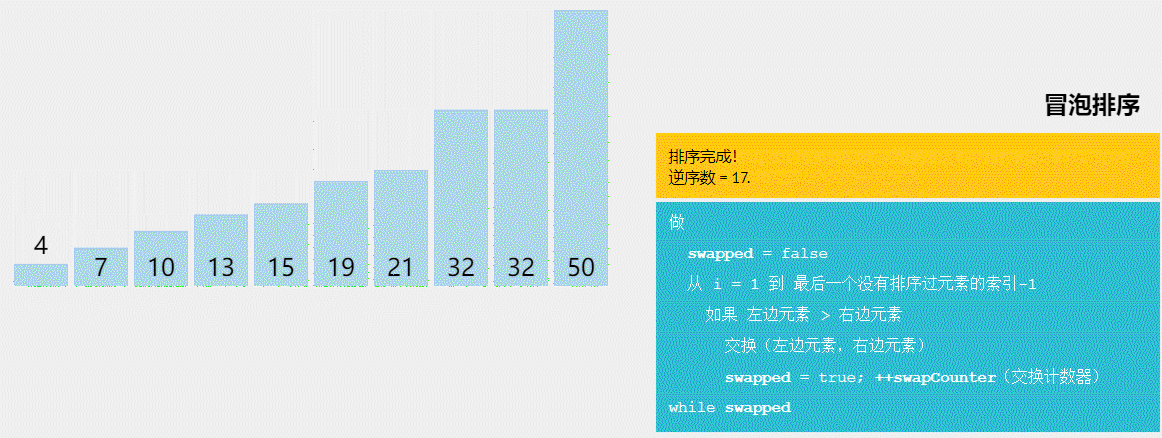本篇文章主要介绍几种经典排序算法:冒泡排序、快速排序、选择排序、堆排序、插入排序、希尔排序、归并排序、桶排序和基数排序。并给出用python实现的算法代码。
目录
一、冒泡排序
二、快速排序
三、选择排序
四、堆排序
五、插入排序
六、希尔排序
七、归并排序
八、桶排序
九、基数排序
一、冒泡排序
冒泡排序如名所见,最大元素像泡泡一样逐渐向上冒,直至顶端(此处指从小到大排序)。最好时间复杂度为O(n),即需排序数组已为有序数组;最坏时间复杂度为O(n²),即需排序数组与要求顺序相反;平均复杂度为O(n²),如下代码所示,两层循环每层时间复杂度均为O(n)。空间复杂度为O(1),无需额外空间消耗,算法稳定。
代码:
def bubbleSort(nums):
for i in range(len(nums)):
is_sort = True
for j in range(len(nums) - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
is_sort = False
if is_sort:
break
return nums解释:
1)设置is_sort判断元素是否已经有序,若元素已完成该轮排序则直接跳出该轮循环进行新一轮排序(即i+1)
2)每轮排序结束,最后一个元素已为最大值(按从小到大顺序排列),下一轮排序则只需对除此之外的元素进行排序:
for j in range(len(nums) - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
其中i为轮次,-1是因为在元素比较时为向后比较(nums[j], nums[j + 1])。
3)算法图解:

图1 冒泡排序算法图解(图源@独影月下酌酒)
二、快速排序
快速排序通过选择“哨兵”结合递归实现排序。最好时间复杂度为O(nlogn),最坏时间复杂度为O(n*n),平均复杂度为O(n*n)。空间复杂度为O(nlogn),算法不稳定。
代码:
def quickSort(nums, left, right):
def partition(nums, left, right):
pivot = nums[left]
while left < right:
while left < right and nums[right] >= pivot:
right -= 1
nums[left] = nums[right]
while left < right and nums[left] <= pivot:
left += 1
nums[right] = nums[left]
nums[left] = pivot
return left
if left < right:
pivotIndex = partition(nums, left, right)
quickSort(nums, left, pivotIndex - 1)
quickSort(nums, pivotIndex + 1, right)
return nums解释:
1)快速排序思想实质上是先找到哨兵,然后对哨兵左右边的元素再进行快速排序。partiton函数即对初始数组进行一次快排并返回哨兵元素的下标,接着主函数调用快排函数本身实现哨兵左右元素的排序。
2)需要注意在partition函数中,先对数组右边元素进行判断,若右边元素大于等于哨兵(pivot),则说明无需移动该元素,右指针左移,直到发现一个哨兵右侧元素小于pivot,此时需要把该元素移到左边,此时将该值赋给左指针指向的位置元素。当pivot右侧元素全都大于等于pivot且右指针仍然在左指针右边时,开始判断pivot左侧元素,当左侧元素小于等于pivot时,左指针右移直到发现某元素大于pivot,将该值赋给右指针指向的位置元素,直到左右指针重合,说明已找到哨兵pivot应放的位置,此时left=right=pivot下标,返回left或right即为pivot位置。
3)在得到哨兵位置后能确定pivot左侧元素均小于哨兵,右侧元素均大于哨兵,此时只需对哨兵左右元素再递归进行快速排序即可。
4)注意大前提left<right
5)算法图解:

图2 快速排序算法图解(图源@独影月下酌酒)
三、选择排序
选择排序即每轮选取一个最小(大)元素放置起始位置,直到所有元素均排序完成。最好时间复杂度为O(n²); 平均时间复杂度为O(n²); 最差时间复杂度为O(n²)。
代码:
def selectSort(nums):
for i in range(len(nums)):
min_index = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[min_index]:
min_index = j
if min_index != i:
nums[min_index], nums[i] = nums[i], nums[min_index]
return nums解释:
1)选择排序没有特别需要注意的地方,弄清算法逻辑就能很快实现。
2)算法图解:

图3 选择排序算法图解(图源@独影月下酌酒)
四、堆排序
堆排序分小顶堆和大顶堆,前者根节点小于左右结点,后者根节点大于左右结点,本文用大顶堆排序。最好时间复杂度为O(nlogn),平均时间复杂度为O(nlogn),最差时间复杂度为O(nlogn)。
代码:
def heap(nums):
def adjustHeap(nums, i, length):
lchild, rchild = 2 * i + 1, 2 * i + 2
largest = i
if lchild < length and nums[lchild] > nums[largest]:
largest = lchild
if rchild < length and nums[rchild] > nums[largest]:
largest = rchild
if largest != i:
nums[largest], nums[i] = nums[i], nums[largest]
adjustHeap(nums, largest, length)
return nums
for i in range(len(nums) // 2)[::-1]:
adjustHeap(nums, i, len(nums))
for i in range(len(nums))[::-1]:
nums[0], nums[i] = nums[i], nums[0]
adjustHeap(nums, 0, i)
return nums解释:
1)拿到一个乱序数组,先将其初始为一个堆(即一棵二叉树),然后调整该堆(adjustHeap函数),使得根节点为最大值 :
for i in range(len(nums) // 2)[::-1]:
adjustHeap(nums, i, len(nums))
堆初始化,从最后一个非叶子节点创建大顶堆
2)堆初始化完成且调整为大顶堆后,交换堆顶元素和需要排序的数组的最后一个元素,调整新数组为大顶堆,如此一来,每一轮调整都能找出此数组中的最大元素,并将其放在数组末端:
for i in range(len(nums))[::-1]:
nums[0], nums[i] = nums[i], nums[0]
adjustHeap(nums, 0, i)
注意:每完成完一轮调整堆,下一次需要调整的数组将不会包括已排序好的元素。
3)调整堆函数(adjustHeap)需要不断判断当前结点的左右结点是否均小于该结点,若出现某一结点大于父结点,则需要将更大的元素调整至父结点,形成一个小型的大顶堆,不断调整至整棵二叉树为一个大顶堆。
if lchild < length and nums[lchild] > nums[largest]:
largest = lchild
if rchild < length and nums[rchild] > nums[largest]:
largest = rchild
if largest != i:
nums[largest], nums[i] = nums[i], nums[largest]
adjustHeap(nums, largest, length)
需要注意的是,在交换完新的更大结点后要重新进行堆调整,以确保每一个小堆均为一个大顶堆。
4)算法图解:


图4 堆排序算法图解(图源@独影月下酌酒)
五、插入排序
插入排序思想很简单,取出一个元素,在已排好序的数组中找到自己要插入的位置放入即可。最好时间复杂度为O(n),平均时间复杂度为O(n²),最差时间复杂度为O(n²)。
代码:
def insertSort(nums):
for i in range(len(nums) - 1):
curNum, preIndex = nums[i + 1], i
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
nums[preIndex + 1] = curNum
return nums解释:
1)curNum和preIndex分别为当前需要插入的元素和其前一个元素下标,若当前元素小于前一个元素,说明该元素应该插在前一个元素之前,即前一个元素需要后移一位,后移完成,preIndex下标需向前移动一位,继续判断当前元素和前一个元素的大小关系,直到与第一个元素比较完成后确定curNum最终应该插入的位置 。
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
nums[preIndex + 1] = curNum
需要注意的是,在最后放curNum时,由于最后一次判断已将preIndex前移了一位,故此时应插入的位置为preIndex + 1。
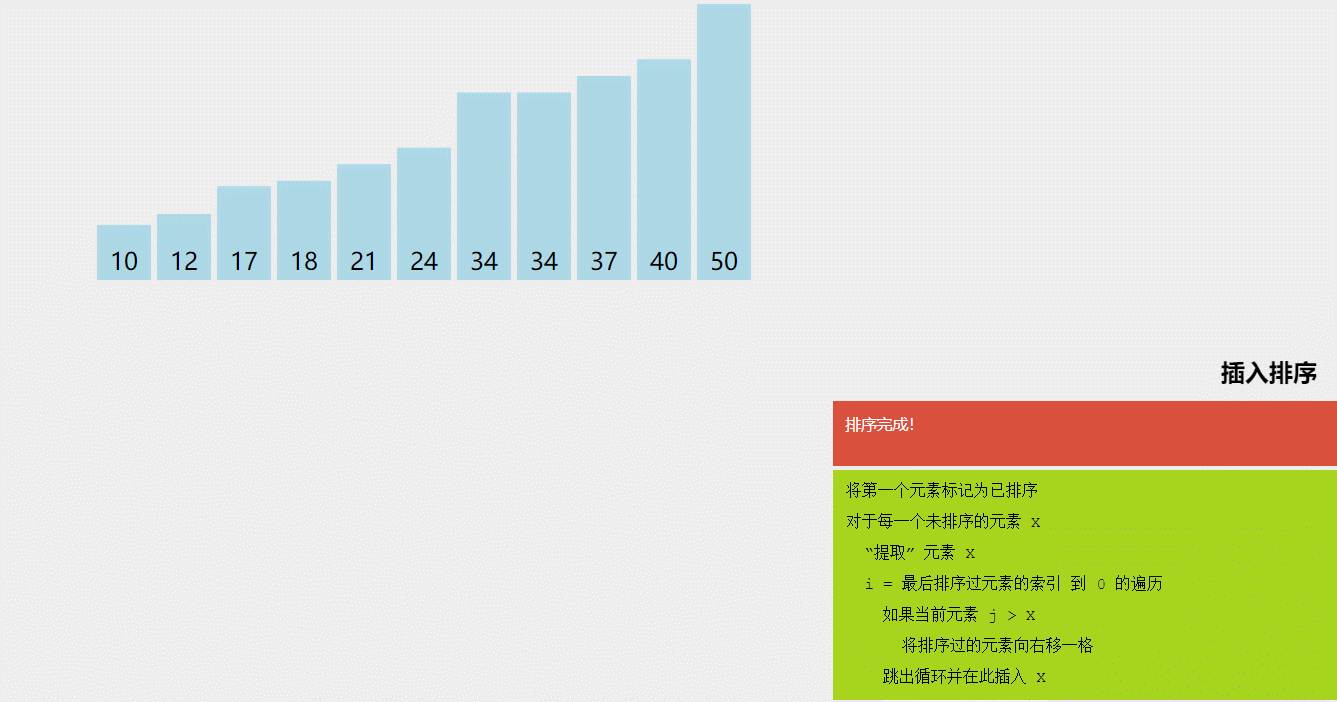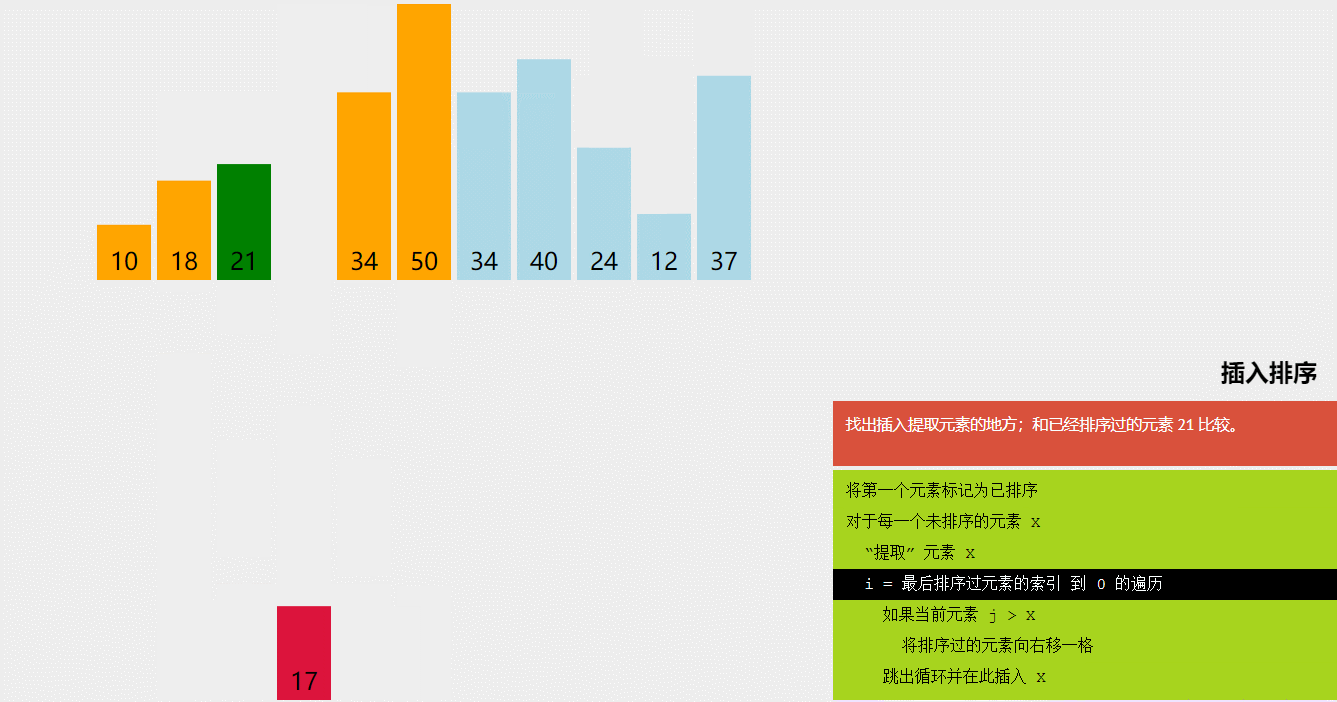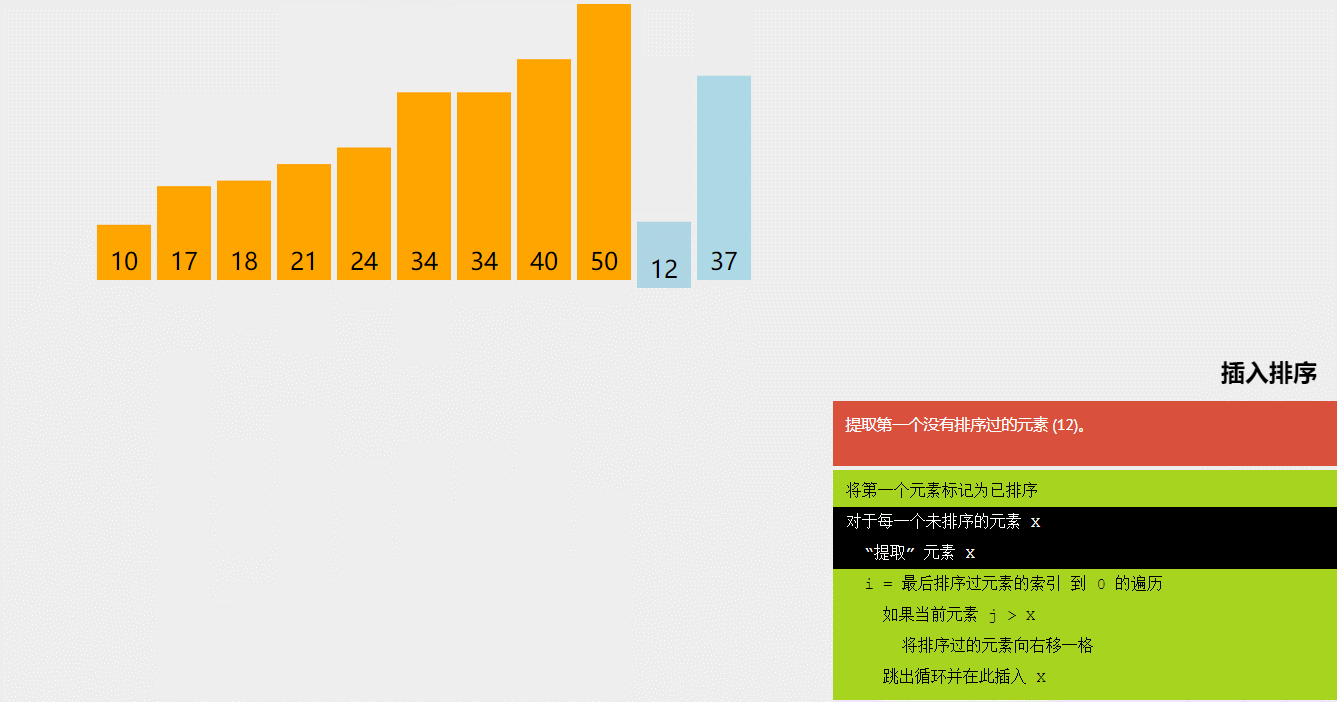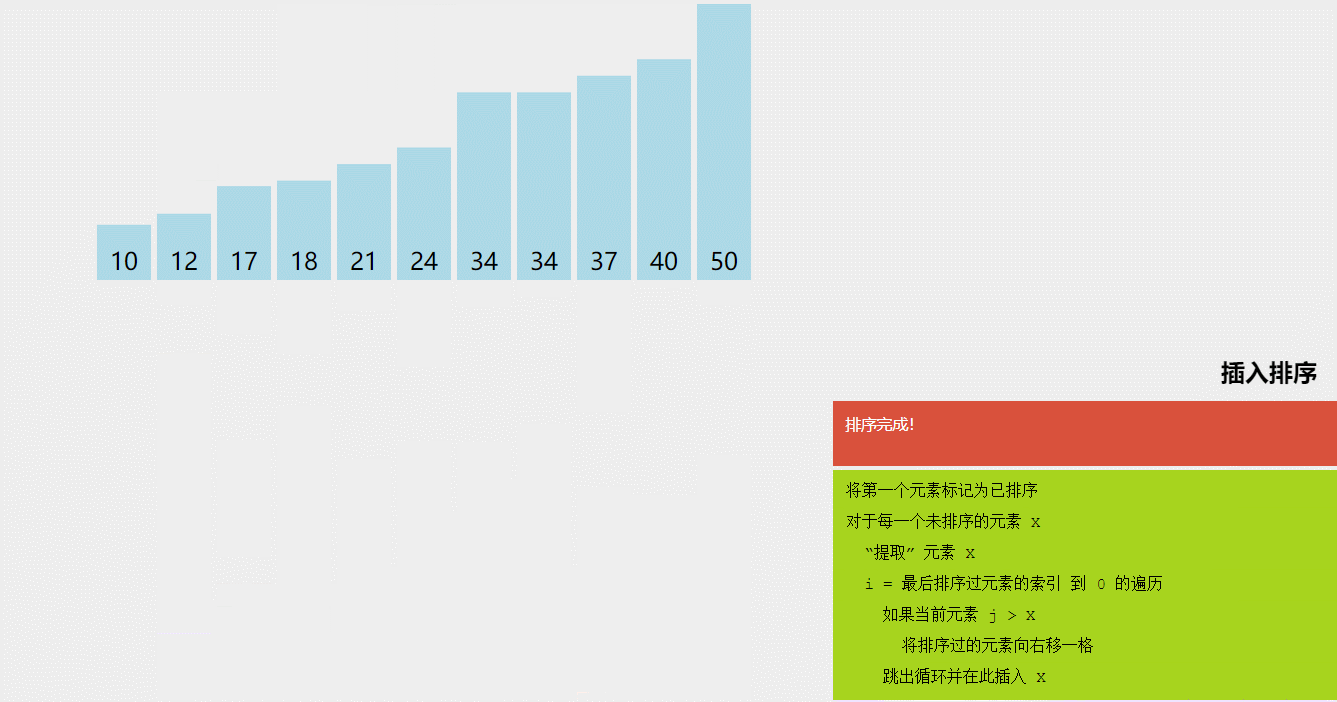
2)算法图解:





图5 插入排序算法图解(图源@独影月下酌酒)
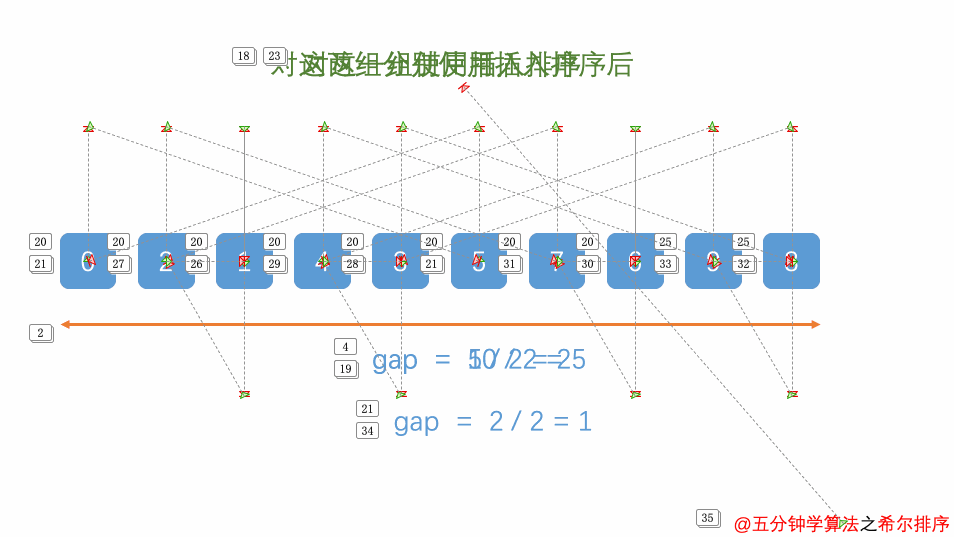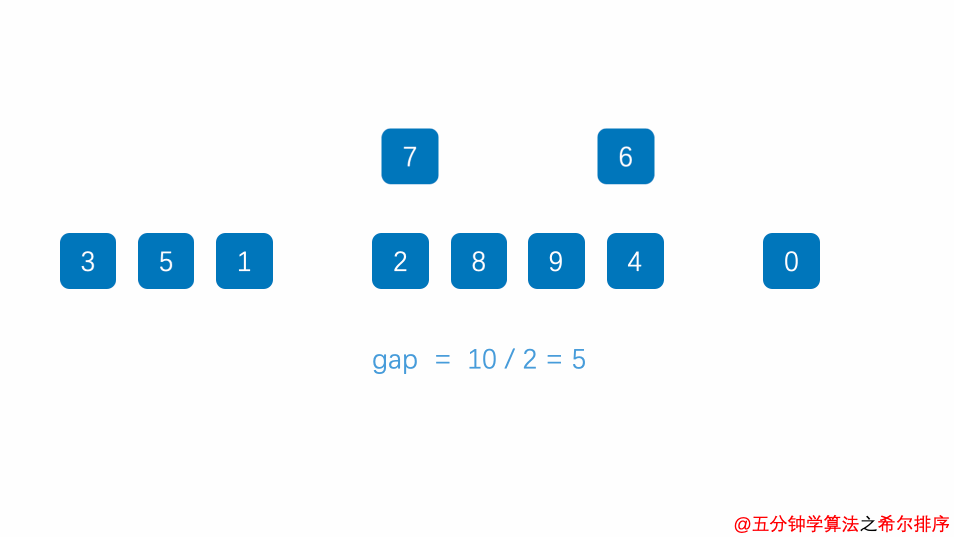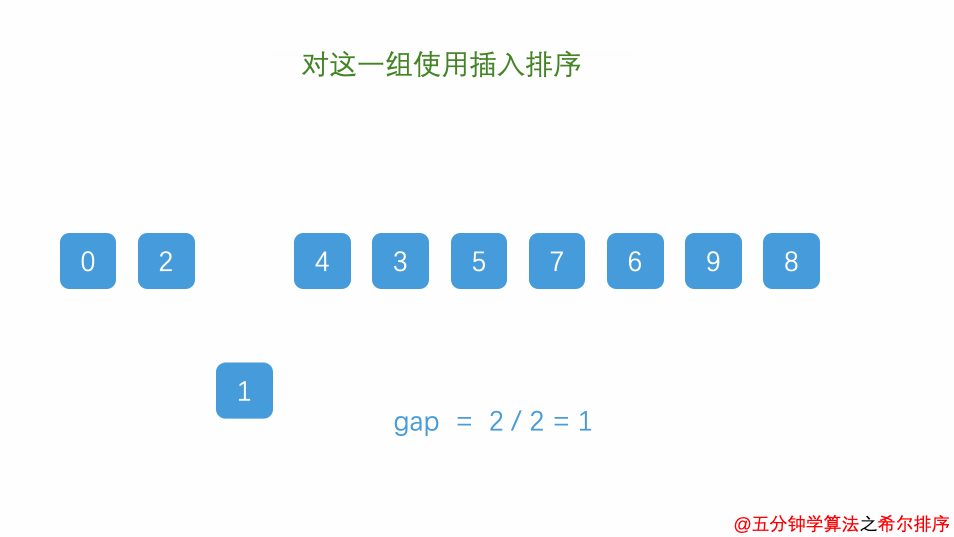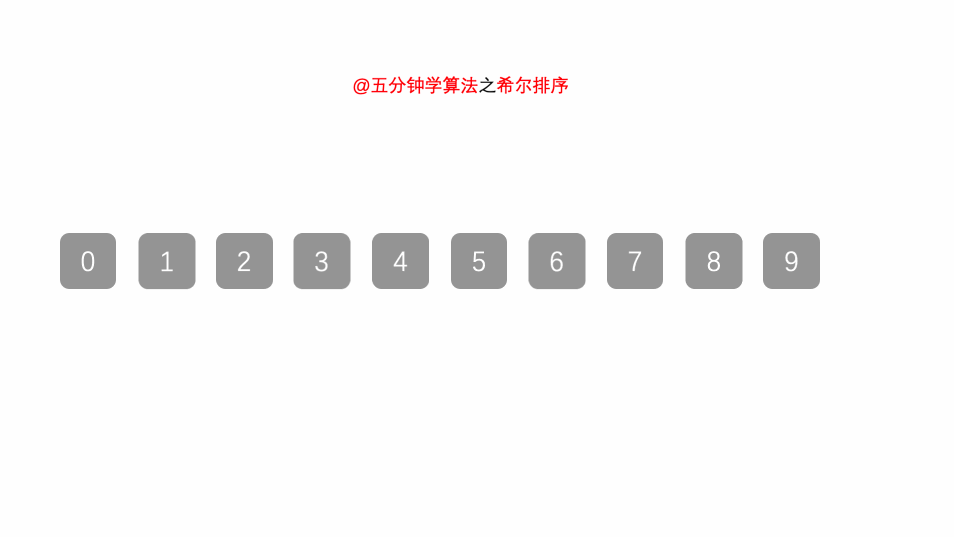
六、希尔排序
希尔排序本质上是插入排序的一种,思想同插入排序一样,不同的的是,希尔排序会先分组,接着组内快速排序,随后不断缩小组间距直至所有元素排序完成。最好时间复杂度为O(n),平均时间复杂度为O(n²),最差时间复杂度为O(n²)。
代码:
def shellSort(nums):
gap = len(nums) // 2
while gap:
for i in range(gap, len(nums)):
curNum, preIndex = nums[i], i - gap
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + gap] = nums[preIndex]
preIndex -= gap
nums[preIndex + gap] = curNum
gap //= 2
return nums解释:
1)gap即为组间距,希尔排序主体仍是快速排序,不断调整组间距直至组间距为0:
while gap:
for i in range(gap, len(nums)):
curNum, preIndex = nums[i], i - gap
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + gap] = nums[preIndex]
preIndex -= gap
nums[preIndex + gap] = curNum
gap //= 2
return nums
注意:与简单的插入排序不同的是,希尔排序的前一个元素下标为 i - gap。
2)算法图解:

图6 希尔排序算法图解(图源@独影月下酌酒)
七、归并排序
归并排序的核心思想即是分而治之,先将数组从中间分为左右两个数组,对左右两个数组进行归并排序后合并左右两个数组即可。
代码:
def mergeSort(nums):
def merge(left, right):
i, j = 0, 0
result = []
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result = result + left[i:] + right[j:]
return result
if len(nums) <= 1:
return nums
mid = len(nums) // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
return merge(left, right)解释:
1)若数组长度<=1则无需排序返回数组本身即可。
2)将需要排序的数组一分为二,分别进行归并排序,即左右子数组分别进行递归(mergeSort)得到两个排序好的数组,最后合并这两个数组即可。
3)合并左右两个数组即设置两个指针分别遍历两个数组,取两者中最小值加入结果数组即可,直到某个数组被遍历完,只需把另一个数组的剩余元素加入结果数组即可(因为两个数组都已事先被排序好了):
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result = result + left[i:] + right[j:]
return result
4)算法图解:

图7 归并排序算法图解(图源@独影月下酌酒)
八、桶排序
桶排序即将数组元素根据某种映射放在各个桶里,先在桶内进行排序,然后将排序好的元素拼接起来即可。最好时间复杂度为O(n+k),最差时间复杂度为O(n²),平均时间复杂度为O(n+k)。
def bucketSort(nums):
def insertSort(nums):
for i in range(len(nums) - 1):
curNum, preIndex = nums[i + 1], i
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
nums[preIndex + 1] = curNum
return nums
bucketSize = 4
bucketCount = (max(nums) - min(nums)) // bucketSize + 1
buckets = [[] for _ in range(bucketCount)]
for num in nums:
buckets[(num - min(nums)) // bucketSize].append(num)
nums.clear()
for bucket in buckets:
insertSort(bucket)
nums.extend(bucket)
return nums解释:
1)根据桶大小和元素分布确定桶个数,初始化桶内元素:
bucketSize = 4
bucketCount = (max(nums) - min(nums)) // bucketSize + 1
buckets = [[] for _ in range(bucketCount)]
2)判断数组元素应该放在哪个桶,将元素全都装桶后清空数组方便放后续排序好的元素:
for num in nums:
buckets[(num - min(nums)) // bucketSize].append(num)
nums.clear()
3)元素装桶完成后进行桶内元素排序,本文桶内元素用的插入排序,然后将排序好的元素全部一起extend到原数组中:
for bucket in buckets:
insertSort(bucket)
nums.extend(bucket)
4)算法图解:

图8 桶排序算法图解(图源@独影月下酌酒)
九、基数排序
基数排序是特殊的桶排序,其根据元素每位数字来分配桶(桶个数为10,分别对应各位取值0~9),按照先低位排序后高位排序的顺序依次排序直到元素有序即可,排序轮次即为数组中最大元素的位数。最好时间复杂度为O(n×k),最差时间复杂度为O(n×k),平均时间复杂度为O(n×k)。
代码:
def radixSort(nums):
mod, div = 10, 1
mostBit = len(str(max(nums)))
buckets = [[] for _ in range(mod)]
while mostBit:
for num in nums:
buckets[num // div % mod].append(num)
i = 0
for bucket in buckets:
while bucket:
nums[i] = bucket.pop(0)
i += 1
div *= 10
mostBit -= 1
return nums解释:
1)mod和div用于取元素各个位数的取值,mostBit是轮次(即元素最大值的位数),buckets个数为10,分别对应各位取值0~9。
2)先将数组中每个元素放到对应桶中,然后按序弹出元素完成第一轮低位排序,接着进行第二轮高位排序,直到所有位均排序完成,此时数组排序完成:
while mostBit:
for num in nums:
buckets[num // div % mod].append(num)
i = 0
for bucket in buckets:
while bucket:
nums[i] = bucket.pop(0)
i += 1
div *= 10
mostBit -= 1
3)算法图解:



图9 基数排序算法图解(图源@独影月下酌酒)
附上@独影月下酌酒的博客以供参考学习:文章来源:https://www.toymoban.com/news/detail-852336.html
Python实现十大排序算法_python排序-CSDN博客文章来源地址https://www.toymoban.com/news/detail-852336.html
到了这里,关于Sorting Algorithms in Python (排序算法)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!