齐次坐标变换的理解以及在无人机相机定位坐标系转换中的应用

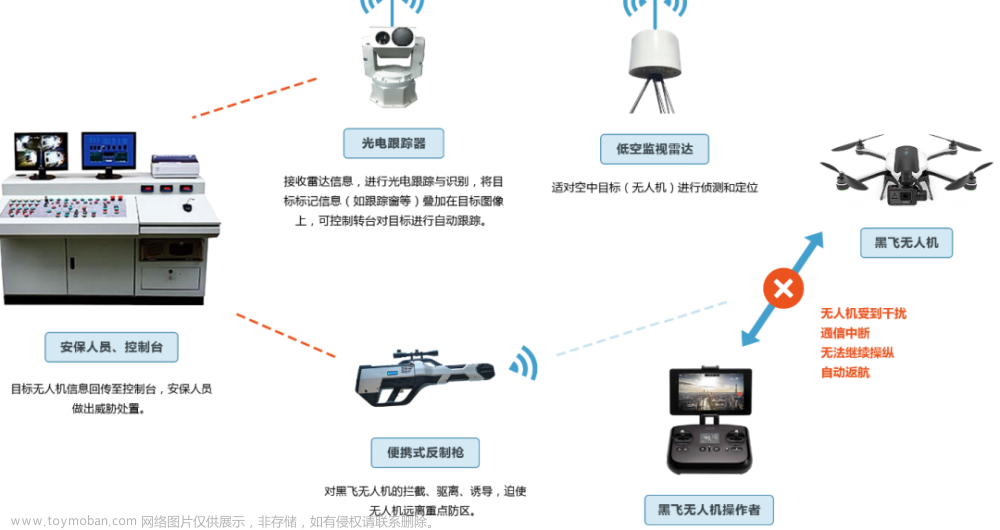
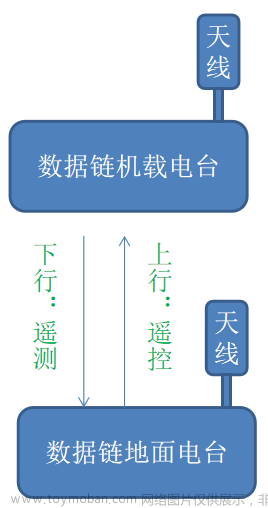
一、平移齐次坐标变换

4*4矩阵的右边三个数表示平移，如果原来的向量u的w=0，那么就是u+（ai+bj+ck）

二、旋转齐次变换矩阵

对应xyz三个轴的循环变换，注意负号的位置

三、物体的变换

用描述空间一点的变换方法来描述物体在空间的位置和方向。

先变换的矩阵乘在右边。

四、齐次变化的逆

五、平移坐标变换

$${}^{A}p={}^{B}p+{}^A{p}_{B_o}$$

从$B$到$A$的平移坐标变换。

问题一

解：

CM先饶$z$轴旋转180°，在沿$x$轴反方向平移0.13m，得到M。
T C M M = T r a n s ( − 0.13 , 0 , 0 ) R o t ( z , 18 0 ° ) = [ 1 0 0 − 0.13 0 1 0 0 0 0 1 0 0 0 0 1 ] [ − 1 0 0 0 0 − 1 0 0 0 0 1 0 0 0 0 1 ] T_{CM}^{M}=Trans\left( -0.13,0,0 \right) Rot\left( z,180^° \right) =\left[ \begin{matrix} 1& 0& 0& -0.13\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \left[ \begin{matrix} -1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] TCMM​=Trans(−0.13,0,0)Rot(z,180°)= ​1000​0100​0010​−0.13001​ ​ ​−1000​0−100​0010​0001​ ​

T C M C = [ R C M C P C M C 0 1 ] = [ cos ⁡ y sin ⁡ y 0 d x − sin ⁡ y cos ⁡ y 0 d y 0 0 1 d z 0 0 0 1 ] T_{CM}^{C}=\left[ \begin{matrix} R_{CM}^{C}& P_{CM}^{C}\\ 0& 1\\ \end{matrix} \right] =\left[ \begin{matrix} \cos y& \sin y& 0& dx\\ -\sin y& \cos y& 0& dy\\ 0& 0& 1& dz\\ 0& 0& 0& 1\\ \end{matrix} \right] TCMC​=[RCMC​0​PCMC​1​]= ​cosy−siny00​sinycosy00​0010​dxdydz1​ ​

齐次矩阵的逆：

T C M M T C C M = [ − cos ⁡ y sin ⁡ y 0 d x cos ⁡ y − d y sin ⁡ y − 0.13 − sin ⁡ y − cos ⁡ y 0 d x sin ⁡ y + d y cos ⁡ y 0 0 1 − d z 0 0 0 1 ] T_{CM}^{M}T_{C}^{CM}=\left[ \begin{matrix} -\cos y& \sin y& 0& dx\cos y-dy\sin y-0.13\\ -\sin y& -\cos y& 0& dx\sin y+dy\cos y\\ 0& 0& 1& -dz\\ 0& 0& 0& 1\\ \end{matrix} \right] TCMM​TCCM​= ​−cosy−siny00​siny−cosy00​0010​dxcosy−dysiny−0.13dxsiny+dycosy−dz1​ ​
把上式代入，得到：
[ x M C M M y M C M M z M C M M 1 ] + T C M M [ x C M C C M y C M C C M z C M C C M 1 ] + T C M M T C C M [ x C B C y C B C z C B C 1 ] \left. \left[ \begin{array}{c} x_{MCM}^{M}\\ y_{MCM}^{M}\\ z_{MCM}^{M}\\ 1\\ \end{array} \right. \right] +T_{CM}^{M}\left[ \begin{array}{c} x_{CMC}^{CM}\\ y_{CMC}^{CM}\\ z_{CMC}^{CM}\\ 1\\ \end{array} \right] +T_{CM}^{M}T_{C}^{CM}\left[ \begin{array}{c} x_{CB}^{C}\\ y_{CB}^{C}\\ z_{CB}^{C}\\ 1\\ \end{array} \right] ​xMCMM​yMCMM​zMCMM​1​ ​+TCMM​ ​xCMCCM​yCMCCM​zCMCCM​1​ ​+TCMM​TCCM​ ​xCBC​yCBC​zCBC​1​ ​

= [ 0.13 0 0 1 ] + [ − 1 0 0 − 0.13 0 − 1 0 0 0 0 1 0 0 0 0 1 ] [ x y z 1 ] + [ − cos ⁡ y sin ⁡ y 0 d x cos ⁡ y − d y sin ⁡ y − 0.13 − sin ⁡ y − cos ⁡ y 0 d x sin ⁡ y + d y cos ⁡ y 0 0 1 − d z 0 0 0 1 ] [ − 0.13 0 0 1 ] =\left[ \begin{array}{l} 0.13\\ 0\\ 0\\ 1\\ \end{array} \right] +\left[ \begin{matrix} -1& 0& 0& -0.13\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \left[ \begin{array}{l} x\\ y\\ z\\ 1\\ \end{array} \right] +\left[ \begin{matrix} -\cos y& \sin y& 0& dx\cos y-dy\sin y-0.13\\ -\sin y& -\cos y& 0& dx\sin y+dy\cos y\\ 0& 0& 1& -dz\\ 0& 0& 0& 1\\ \end{matrix} \right] \left[ \begin{array}{c} -0.13\\ 0\\ 0\\ 1\\ \end{array} \right] = ​0.13001​ ​+ ​−1000​0−100​0010​−0.13001​ ​ ​xyz1​ ​+ ​−cosy−siny00​siny−cosy00​0010​dxcosy−dysiny−0.13dxsiny+dycosy−dz1​ ​ ​−0.13001​ ​

= [ − x + d x cos ⁡ y − d y sin ⁡ y + 0.13 cos ⁡ y − 0.13 − y + d x sin ⁡ y + d y cos ⁡ y + 0.13 sin ⁡ y z + d z 1 ] =\left[ \begin{array}{c} -x+dx\cos y-dy\sin y+0.13\cos y-0.13\\ -y+dx\sin y+dy\cos y+0.13\sin y\\ z+dz\\ 1\\ \end{array} \right] = ​−x+dxcosy−dysiny+0.13cosy−0.13−y+dxsiny+dycosy+0.13sinyz+dz1​ ​

注意到，在$dt$时间内，$dx,dy$是小量，可以略去，剩下的部分就是如下代码：文章来源地址https://www.toymoban.com/news/detail-852345.html

(r,p,y)=tf.transformations.euler_from_quaternion([data.pose.pose.orientation.x,data.pose.pose.orientation.y,data.pose.pose.orientation.z,data.pose.pose.orientation.w])
local_pose.pose.position.x = -data.pose.pose.position.x - rtt_ctr_b * (1-math.cos(y))
local_pose.pose.position.y = - data.pose.pose.position.y + rtt_ctr_b * math.sin(y) #推导y
local_pose.pose.position.z = data.pose.pose.position.z            #相机高度作为无人机的高度
local_pose.pose.orientation =  data.pose.pose.orientation

到了这里，关于齐次坐标变换的理解以及在无人机相机定位坐标系转换中的应用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！