【并集查找图论位运算】3108. 带权图里旅途的最小代价-Toy模板网

这篇具有很好参考价值的文章主要介绍了【并集查找图论位运算】3108. 带权图里旅途的最小代价。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

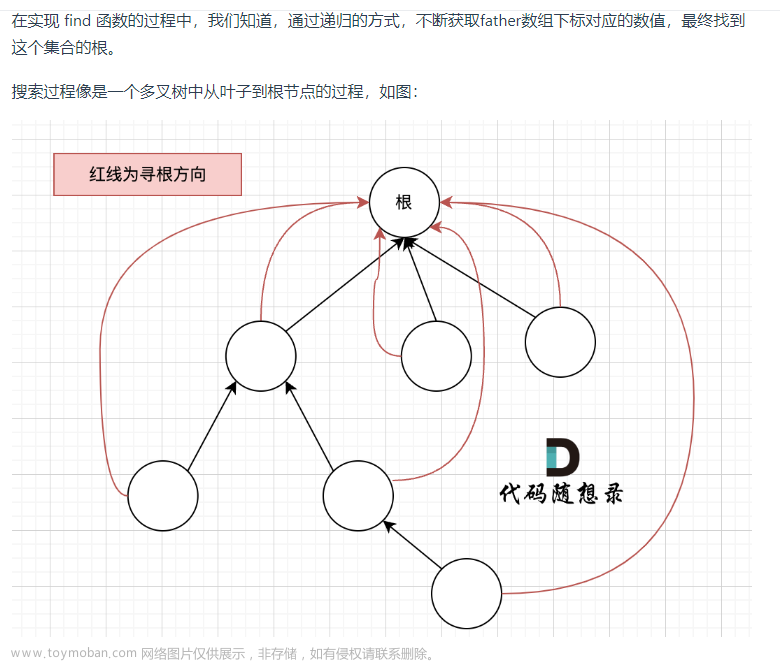
算法可以发掘本质，如：
一，若干师傅和徒弟互有好感，有好感的师徒可以结对学习。师傅和徒弟都只能参加一个对子。如何让对子最多。
二，有无限多1X2和2X1的骨牌，某个棋盘若干格子坏了，如何在没有坏的格子放足够多骨牌。
三，某个单色图，1表示前前景，0表示后景色。每次操作可以将一个1，变成0。如何在最少得操作情况下，使得没有两个1相邻（四连通）。
四，若干路人，有些人是熟人，如何选出最多的人参加实验。为了避免熟人影响实验的效果，参加的人不能是熟人。
一二是二分图的最大匹配，三是二分图的最小点覆盖，四是二分图最大独立集。而这三者是等效问题。

本文涉及知识点

并集查找图论位运算

LeetCode3108. 带权图里旅途的最小代价

给你一个 n 个节点的带权无向图，节点编号为 0 到 n - 1 。
给你一个整数 n 和一个数组 edges ，其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。
在图中，一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点，且图中存在连接旅途中相邻节点的边。注意，一趟旅途可能访问同一条边或者同一个节点多次。
如果旅途开始于节点 u ，结束于节点 v ，我们定义这一趟旅途的代价是经过的边权按位与 AND 的结果。换句话说，如果经过的边对应的边权为 w0, w1, w2, …, wk ，那么代价为w0 & w1 & w2 & … & wk ，其中 & 表示按位与 AND 操作。
给你一个二维数组 query ，其中 query[i] = [si, ti] 。对于每一个查询，你需要找出从节点开始 si ，在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途，答案为 -1 。
返回数组 answer ，其中 answer[i] 表示对于查询 i 的最小旅途代价。

示例 1：

输入：n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

输出：[1,-1]

解释：
【并集查找图论位运算】3108. 带权图里旅途的最小代价,# 算法题,图论,算法,c++,力扣,位运算,并集查找,位与

第一个查询想要得到代价为 1 的旅途，我们依次访问：0->1（边权为 7 ）1->2 （边权为 1 ）2->1（边权为 1 ）1->3 （边权为 7 ）。

第二个查询中，无法从节点 3 到节点 4 ，所以答案为 -1 。

示例 2：

输入：n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]
【并集查找图论位运算】3108. 带权图里旅途的最小代价,# 算法题,图论,算法,c++,力扣,位运算,并集查找,位与

输出：[0]

解释：

第一个查询想要得到代价为 0 的旅途，我们依次访问：1->2（边权为 1 ），2->1（边权为 6 ），1->2（边权为 1 ）。

提示：

1 <= n <= 10⁵
0 <= edges.length <= 10⁵
edges[i].length == 3
0 <= ui, vi <= n - 1
ui != vi
0 <= wi <= 10⁵
1 <= query.length <= 10⁵
query[i].length == 2
0 <= si, ti <= n - 1

并集查找

两个数位与不会变大，只会不变或变小。要想旅途代价最小就要尽可能的多进过边，把能经过的边全部经过一遍。也就是连通区域所有的边。
vMin[node] 是经过node所有边的位与和。
vGroupMin[iGroup]是本连通区域所有边的位与和。

代码

核心代码

class CUnionFind
{
public:
	CUnionFind(int iSize) :m_vNodeToRegion(iSize)
	{
		for (int i = 0; i < iSize; i++)
		{
			m_vNodeToRegion[i] = i;
		}
		m_iConnetRegionCount = iSize;
	}	
	CUnionFind(vector<vector<int>>& vNeiBo):CUnionFind(vNeiBo.size())
	{
		for (int i = 0; i < vNeiBo.size(); i++) {
			for (const auto& n : vNeiBo[i]) {
				Union(i, n);
			}
		}
	}
	int GetConnectRegionIndex(int iNode)
	{
		int& iConnectNO = m_vNodeToRegion[iNode];
		if (iNode == iConnectNO)
		{
			return iNode;
		}
		return iConnectNO = GetConnectRegionIndex(iConnectNO);
	}
	void Union(int iNode1, int iNode2)
	{
		const int iConnectNO1 = GetConnectRegionIndex(iNode1);
		const int iConnectNO2 = GetConnectRegionIndex(iNode2);
		if (iConnectNO1 == iConnectNO2)
		{
			return;
		}
		m_iConnetRegionCount--;
		if (iConnectNO1 > iConnectNO2)
		{
			UnionConnect(iConnectNO1, iConnectNO2);
		}
		else
		{
			UnionConnect(iConnectNO2, iConnectNO1);
		}
	}

	bool IsConnect(int iNode1, int iNode2)
	{
		return GetConnectRegionIndex(iNode1) == GetConnectRegionIndex(iNode2);
	}
	int GetConnetRegionCount()const
	{
		return m_iConnetRegionCount;
	}
	vector<int> GetNodeCountOfRegion()//各联通区域的节点数量
	{
		const int iNodeSize = m_vNodeToRegion.size();
		vector<int> vRet(iNodeSize);
		for (int i = 0; i < iNodeSize; i++)
		{
			vRet[GetConnectRegionIndex(i)]++;
		}
		return vRet;
	}
	std::unordered_map<int, vector<int>> GetNodeOfRegion()
	{
		std::unordered_map<int, vector<int>> ret;
		const int iNodeSize = m_vNodeToRegion.size();
		for (int i = 0; i < iNodeSize; i++)
		{
			ret[GetConnectRegionIndex(i)].emplace_back(i);
		}
		return ret;
	}
private:
	void UnionConnect(int iFrom, int iTo)
	{
		m_vNodeToRegion[iFrom] = iTo;
	}
	vector<int> m_vNodeToRegion;//各点所在联通区域的索引,本联通区域任意一点的索引，为了增加可理解性，用最小索引
	int m_iConnetRegionCount;
};


class Solution {
public:
	vector<int> minimumCost(int n, vector<vector<int>>& edges, vector<vector<int>>& query) {
		CUnionFind uf(n);
		vector<int> vMin(n,(1<<20)-1);
		for (const auto& v : edges) {
			uf.Union(v[0], v[1]);
			vMin[v[0]] &= v[2];
			vMin[v[1]] &= v[2];
		}
		auto m = uf.GetNodeOfRegion();
		vector<int> vGroupMin = vMin;
		for (const auto& [group, v] : m) {
			for (const auto& node : v) {
				vGroupMin[group] &= vMin[node];
			}			
		}

		vector<int> vRet;
		for (const auto& v : query) {
			if (uf.IsConnect(v[0], v[1])) {
				const int iGroup = uf.GetConnectRegionIndex(v[0]);
				vRet.emplace_back(vGroupMin[iGroup]);
			}
			else {
				vRet.emplace_back(-1);
			}
		}
		return vRet;
	}
};

【并集查找图论位运算】3108. 带权图里旅途的最小代价,# 算法题,图论,算法,c++,力扣,位运算,并集查找,位与

扩展阅读

视频课程

有效学习：明确的目标及时的反馈拉伸区（难度合适），可以先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

我想对大家说的话
闻缺陷则喜是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛