机器人坐标系转换从局部坐标系转换到世界坐标系-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器人坐标系转换从局部坐标系转换到世界坐标系。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

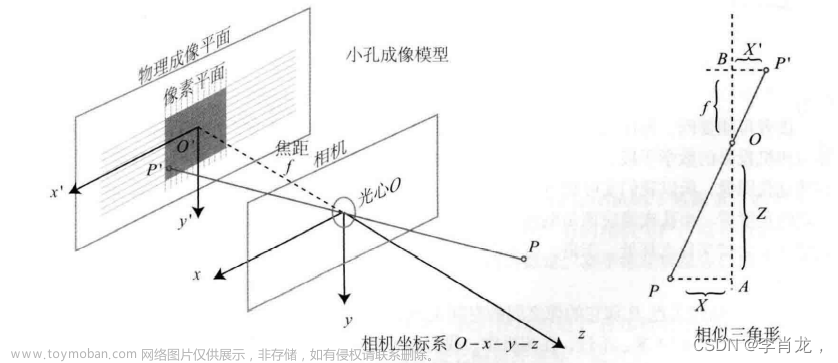
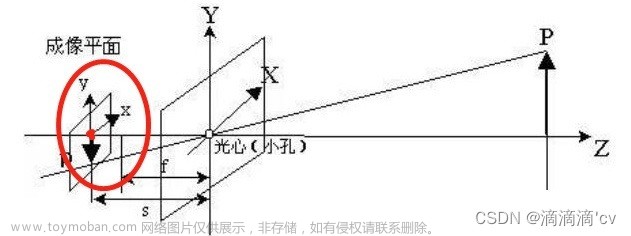
矩阵方式：
机器人坐标转换世界坐标,机器人
下面是代码：

#include <Eigen/Dense>

static void transLocalToWorldCloudWith2dPose(const PointCloud &pc_tar, const QPose3f &pose, PointCloud &pc_org) {
    if (pc_tar.empty())
        return;

    PointCloud tmp_pc;
    Eigen::Rotation2Dd R(-pose.yaw);  // 创建旋转矩阵
    Eigen::Vector2d d(pose.x, pose.y);  // 创建平移向量

    for (const auto& point : pc_tar) {
        Eigen::Vector2d local_point(point.x, point.y);
        Eigen::Vector2d world_point = R * local_point + d;  // 进行坐标转换

        tmp_pc.push_back(PointPCL(world_point.x(), world_point.y(), point.z));
    }

    pcl::copyPointCloud(tmp_pc, pc_org);
}

// 在调用此函数时：
transLocalToWorldCloudWith2dPose(pc_tar, pose, pc_org);

函数方式：
机器人坐标转换世界坐标,机器人
根据三角函数的特性，可以进行一下简化：

下面是简化前的代码示例：文章来源地址https://www.toymoban.com/news/detail-852737.html

static void transLocalToWorldCloudWith2dPose(const PointCloud &pc_tar, const QPose3f &pose, PointCloud &pc_org) {
    if (pc_tar.empty())
        return;

    PointCloud tmp_pc;
    for (const auto& point : pc_tar) {
        double world_x;
        double world_y;
        double d_x = point.x * cos(-pose.yaw) + point.y * sin(-pose.yaw);
        double d_y = -point.x * sin(-pose.yaw) + point.y * cos(-pose.yaw);
        world_x = d_x + pose.x;
        world_y = d_y + pose.y;
        tmp_pc.push_back(PointPCL(world_x, world_y, point.z));
    }

    pcl::copyPointCloud(tmp_pc, pc_org);
}

// 在调用此函数时：
transLocalToWorldCloudWith2dPose(pc_tar, pose, pc_org);