动态规划：完全背包问题----中专生刷算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划：完全背包问题----中专生刷算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

动态规划：完全背包问题----中专生刷算法,算法,动态规划,蓝桥杯,c++,学习

需要基础:闫氏dp分析法，01背包问题

先去看一下01背包问题，再看完全背包

动态规划:选择dp及优化01背包问题-CSDN博客

做过01背包问题的同学会发现,完全背包问题的代码

在01背包基础上改动很小，但是里面的思想，有很大差距

题目

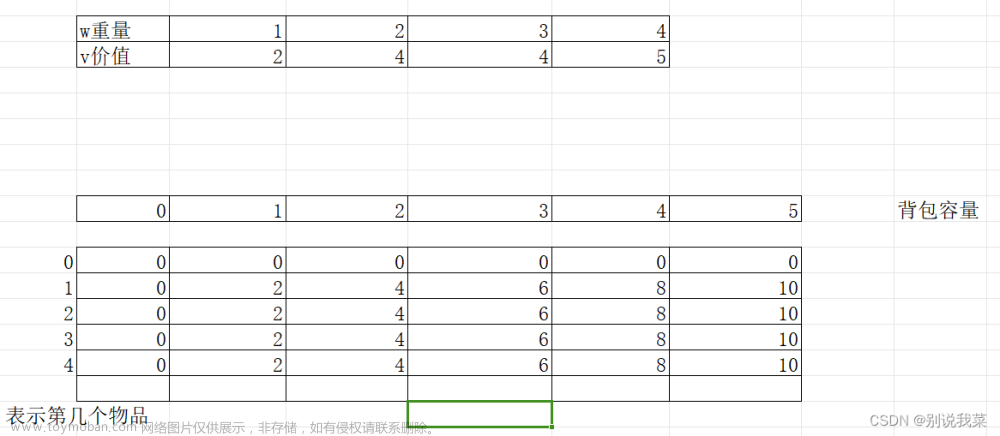
有 N 种物品和一个容量是 V的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000

0<vi,wi≤1000

输入样例

输出样例：

完全背包和01背包区别

完全背包每种物品都有无限件可用

思路

在闫氏dp分析法中，完全背包问题和01背包问题主要区分在状态计算区别

01背包图链接01背包图

以及图文详解01背包动态规划:选择dp及优化01背包问题-CSDN博客

完全背包问题分析图

动态规划：完全背包问题----中专生刷算法,算法,动态规划,蓝桥杯,c++,学习

我们发现，这次的完全背包，需要三重循环，时间复杂度太高

1层循环枚举从前i个数选，2层循环枚举容量为j时，3层循环枚举第i个数选多少个

我们需要优化算法。减少时间复杂度。

可以发现，如果我们每次都是选出的max，那么在决定选几个i时，我们不需要穷举

因为在第二层j循环，f[i][j-v[i]]代表的就是在容量在[j-v[i]]时在前i个数里选的最大价值

f[i][j-v[i]]里面可能已经选了n个vi，也可能没选，这时候给f[i][j-v[i]]加上w[i]，表示再选择一个i

那一定是选k(k!=0)个i的最大价值，就不需要通过没选i时的f[i-1][*]来进行计算选多少i

通过f[i][j-v[i]]+w[i]，即是此轮选k个vi(k!=0)的最大值

f[i-1][j]表示的是容量为j,不选i的选法的最大价值

f[i][j-v[i]]+w[i]表示的是容量为j，选k(k!=0)个i的选法的最大价值

则分析图变成如下

动态规划：完全背包问题----中专生刷算法,算法,动态规划,蓝桥杯,c++,学习

代码实现

#include<iostream>
using namespace std;
//f[i][j],i表示从前i个数里选，j表示容量
int f[1010][1010];//f[i][j]表示从前i个数里选，在容量为j时最优价值最大选法
int u[1010],w[1010];//u体积，w价值
int main(){
    int N,V;
    cin>>N>>V;
    //读入价值和重量，i从1开始，防止双层循环内i-1越界
    for(int i=1;i<=N;i++)cin>>u[i]>>w[i];
     //遍历每种状态表示下的集合属性（最大价值）
    for(int i=1;i<=N;i++){//从1开始，前0个数无意义，而且会造成i-1越界
     //容量从0开始，每次内层循环，算出前i个数在容量为V时的最大价值
    //这个数是f[i][V],则f[N][V],是N个数在V容量内最大价值
        for(int j=0;j<=V;j++){
            //和前缀和有点像，前缀和保存的是累加和，f[i][j]保存的是最大价值
            //上轮外层循环时得出过f[i-1][j]的最大价值，也就是容量j，不选i的最大价值
            //直接取用
            f[i][j]=f[i-1][j];
             //先判断，避免目前容量无法存储i的体积
             //f[i][j]在max函数做参数时的值是f[i-1][j]
             //f[i][j-u[i]]+w[i]是选k(不为0，不固定)个i时的最大价值
             //f[i-1][j]和f[i][j-u[i]]+w[i]比较，结果就是f[i][j]的最大价值
            if(u[i]<=j)f[i][j]=max(f[i][j],f[i][j-u[i]]+w[i]);
        }
    }
    cout<<f[N][V];
    return 0;
}

优化代码空间复杂度

#include<iostream>
using namespace std;
int f[1010];//降为1维
int u[1010],w[1010];//u体积，w价值
int main(){
    int N,V;
    cin>>N>>V;
    for(int i=1;i<=N;i++)cin>>u[i]>>w[i];
    for(int i=1;i<=N;i++){
        for(int j=0;j<=V;j++){
            //f[i][j]=f[i-1][j]等价于f[j]=f[j]，因为f[i][j]还没更新;
            //f[i][j]现在的值就是f[i-1][j]
            f[j]=f[j];
            //优化if(u[i]<=j)f[i][j]=max(f[i][j],f[i][j-u[i]]+w[i]);
            //f[i][j]优化为f[j]10,11行注释已经解释
            //f[i][j-u[i]]+w[i]优化为f[j-u[i]]+w[i]
            //这里的j是从小到大循环,所以f[j-u[i]]一定已经遍历过，而且被更新了
            //所以f[i][j-u[i]]+w[i]等价于f[j-u[i]]+w[i]
            //总结，f[j]因为没更新过，所以f[j]=f[i-1][j]
            //f[j-u[i]]更新过了，f[j-u[i]]=f[i][j-u[i]]
            if(u[i]<=j)f[j]=max(f[j],f[j-u[i]]+w[i]);
        }
    }
    cout<<f[V];
    return 0;
}

优化代码写法

f[j]=f[j];可以舍弃，无效代码

21行判断可以写到循环内，让j从u[i]开始遍历，就没有j<u[i]的情况了文章来源地址https://www.toymoban.com/news/detail-853003.html

最终代码

#include<iostream>
using namespace std;
int f[1010];
int u[1010],w[1010];
int main(){
    int N,V;
    cin>>N>>V;
    for(int i=1;i<=N;i++)cin>>u[i]>>w[i];
    for(int i=1;i<=N;i++)
        for(int j=u[i];j<=V;j++)
            f[j]=max(f[j],f[j-u[i]]+w[i]);
    cout<<f[V];
    return 0;
}