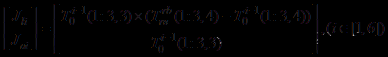文章目录
目录
文章目录
前言
一、复变函数导数
1.1 导数定义
1.2 求导法则
1.3 存在条件
二、常用求导结论
2.1 标量函数对标量的导数
2.2 标量函数对矢量的导数
2.3 标量函数对矩阵的导数
总结
前言
本文将从信号处理的角度简单阐明复变函数理论的重要性,并重点介绍能够用于信号处理领域的复变函数求导原理。
能够发射到空间中的信号只能是实信号。然而我们在处理接收信号时,往往是复信号形式的,这两者并不冲突。实信号频谱是左右对称的,也就是实信号有至少一半频谱携带的信息是冗余的,为了提高频谱利用率,IQ调制与解调技术被用于信号的发射与接收,接收的信号分为IQ两路信号。为了更好更高效的描述IQ信号,人们提出利用复变函数来描述IQ两路信号(复信号实际是不存在的,它只是描述IQ两路信号的最佳手段)。因此,基于实变函数的理论在复数中不再适用,包括估计理论中克拉美罗界的推导、匹配滤波理论的推导等需要从复变函数的角度重新开展,而其中一个重要的基础理论就是复变函数的求导理论。
一、复变函数导数
1.1 导数定义
设在点的某邻域内有定义,且,其中。若下面极限存在
则称在点可导,其极限值称为在点的导数,记为或。
1.2 求导法则
复变函数和在复变量区域D内处处可导,则下列运算规则得到的复变函数的导数为
1)和差法则
2) 积法则
3) 商法则
4) 链式法则
若函数和分别在区域G和D内可导,且将D映射为使得,则复合函数在D内可导,且
5) 反函数法则
若函数在区域D内可导且将D一一映射到区域E。若在区域D内且反函数在E连续,则在E内可导,且
1.3 存在条件
复变函数在点
可导的充要条件是函数,在点可微(四个一阶偏导数在该点存在且连续),其满足方程(Cauchy-Riemann方程)
当在点可导时,在该点有
- 证明
假设在可导,则有
进一步有
上式等价于
上式分别表示,的微分形式,因此在可导等价于
- 扩展1
利用,导数可以表示为
- 扩展2
,则存在的等效条件为
对应导数为:
- 推论
导数如果存在且不等于0,则导数必然不存在。(该结论是博主根据上述结论得到的新结论,没有细致调研,因此无法判断该结论是否有人证明过,感兴趣的可以去调研,也希望在评论区给出调研结果以及结论的证明过程)
二、常用求导结论
2.1 标量函数对标量的导数
标量是复变量的复变函数,下面为常见复变函数的导数:
注:该式的导数是不存在的(不满足C-R方程),为了方便分析,一般认为和是相互独立的两个变量
表示实变量,下面为常见实变函数的导数:
2.2 标量函数对矢量的导数
为复矢量,为复矢量的标量函数,和都为复矢量的矢量函数,并作出如下导数定义
,
则
为实矢量,为实矢量的实函数,和都为实矢量的矢量函数,则
2.3 标量函数对矩阵的导数
和分别是和的矩阵,则
,,,
表示方阵对角线上元素之和,称为迹。表示行列式。

祝同江等. 工程数学复变函数(第三版).北京:电子工业出版社,2012.6.
复数矩阵求导辨识 - 知乎 (zhihu.com)
标量函数对矢量的求导 - 百度文库 (baidu.com)
复数矩阵求导的转置和共轭转置问题?(MMSE预编码器推导) - 知乎 (zhihu.com)文章来源:https://www.toymoban.com/news/detail-853004.html
总结
本文简单介绍了复变函数的求导,用于信号处理领域的研究。有问题也欢迎评论区留言。转载请附链接【杨(_> <_)】-CSDN博客。文章来源地址https://www.toymoban.com/news/detail-853004.html
到了这里,关于复变函数导数求解(包含矢量、矩阵形式)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!