动态规划（01背包问题）-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划（01背包问题）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文默认读者具有动态规划前置知识

动态规划的特点：

重叠子问题
状态转移方程
最优子结构

题型：求最值
解题套路：

明确【状态】
明确【选择】
明确dp函数/数据的定义
明确base case

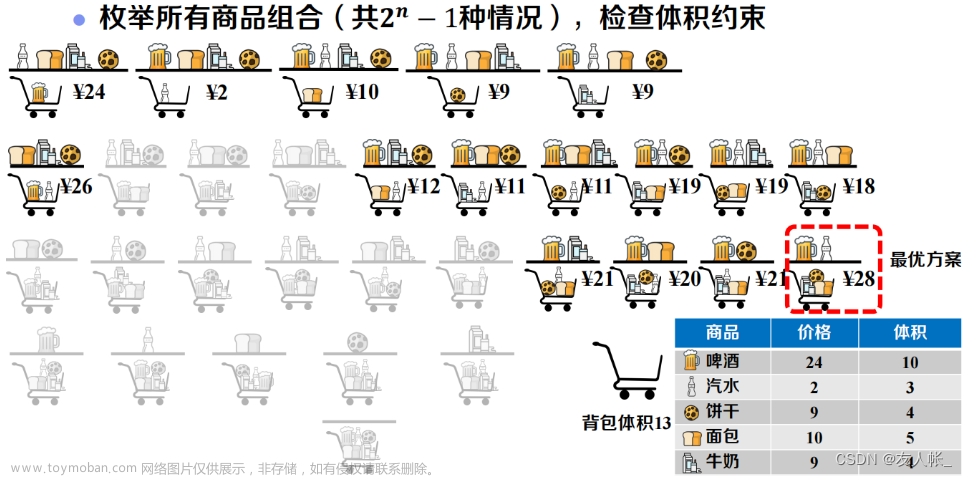
例：给你一个可装载容量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为va[i]，现在让你用这个背包装物品，最多能装的价值是多少?
在这里将问题具体化：现在有4 (N=4)个物品，背包总容量为8 (W=8),背包最多能装入价值为多少的物品?

物体编号	物体体积	物体价值
1	2	3
2	3	4
3	4	5
4	5	6

第一步，明确状态和选择
状态：背包的空余容量剩多少；可选择的物品还有哪些
选择：把这个物品装进背包；把这个物品装进背包
第二步，明确dp数组的定义：对于前1个物品，当背包的容量为w时，可以装的最大价值是 dp[i][w]
比如说，dp[4][8]=10的含义为:
对于给定的一系列物品中，若只对前4个物品进行选择，当背包容量为8时，最多可以装下的价值为10。
根据此定义，还可得出:base case为dp[0][…] = dp[…][0] =0（编号为0，不装物品；容量为0，装不下任何物体），我们想计算的结果是 dp[N][W]
背包容量为1，物品编号可选为1，通过上表可知，物品编号为1时物品体积为2，所以此时选择不装任何物品。
背包容量为2，物品编号可选为1，装入则价值为3。依次往后填充该行。
背包容量为3，物品编号可选为1、2时，装入编号为2的物品，此时价值为4。
背包容量为5，物品编号可选为1、2时，装入编号为1和2的物品，此时价值为7。
依次往后填充完该表格
第三步，根据[选择]写出状态转移逻辑：在w的约束下，把物品i装进背包,最大价值是多少；在w的约束下，不把物品i装进背包，最大价值是多少?文章来源地址https://www.toymoban.com/news/detail-853298.html

for(let i=1;i<=n;i++) {
    for(let v=w[i]; v<=c;v++) {
      dp[i][v] = Math.max(dp[i-1][v], dp[i-1][v-w[i]]+value[i])
    }
}

背包问题完整求解代码：

// 入参是物品的个数和背包的容量上限，以及物品的重量和价值数组
function knapsack(n, c, w, value) {
    // dp是动态规划的状态保存数组
    const dp = (new Array(c+1)).fill(0)  
    // res 用来记录所有组合方案中的最大值
    let res = -Infinity
    for(let i=1;i<=n;i++) {
        for(let v=c;v>=w[i];v--) {
            // 写出状态转移方程
            dp[v] = Math.max(dp[v], dp[v-w[i]] + value[i])
            // 即时更新最大值
            if(dp[v] > res) {
                res = dp[v]
            }
        }
    }
    return res
}

扩展 – 最长上升子序列模型

题目描述：给定一个无序的整数数组，找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

代码实现

/**
 * @param {number[]} nums
 * @return {number}
 */
// 入参是一个数字序列
const lengthOfLIS = function(nums) {
  // 缓存序列的长度
  const len = nums.length  
  // 处理边界条件
  if(!len) {
      return 0
  }
  // 初始化数组里面每一个索引位的状态值
  const dp = (new Array(len)).fill(1)
  // 初始化最大上升子序列的长度为1
  let maxLen = 1 
  // 从第2个元素开始，遍历整个数组
  for(let i=1;i<len;i++) {
      // 每遍历一个新元素，都要“回头看”，看看能不能延长原有的上升子序列
      for(let j=0;j<i;j++) {  
          // 若遇到了一个比当前元素小的值，则意味着遇到了一个可以延长的上升子序列，故更新当前元素索引位对应的状态
          if(nums[j]<nums[i]) {
              dp[i] = Math.max(dp[i], dp[j] + 1)  
          }
      }
      // 及时更新上升子序列长度的最大值
      if(dp[i] > maxLen) {
          maxLen = dp[i]
      }
  }
  // 遍历完毕，最后到手的就是最大上升子序列的长度
  return maxLen
};