2.3.5 基于自适应反演滑模控制器的仿真测试
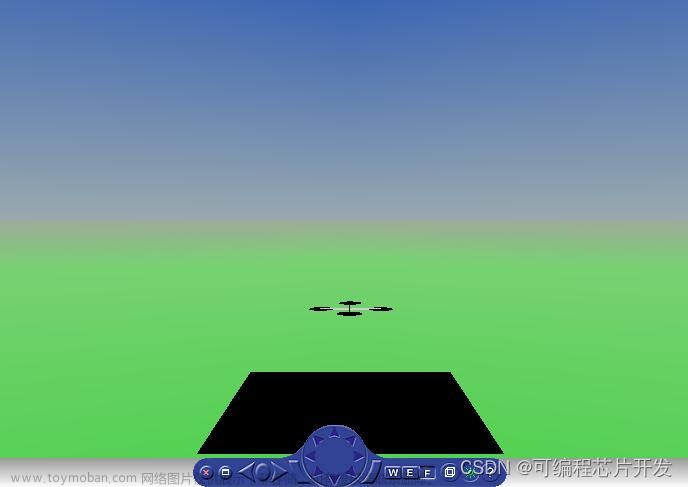
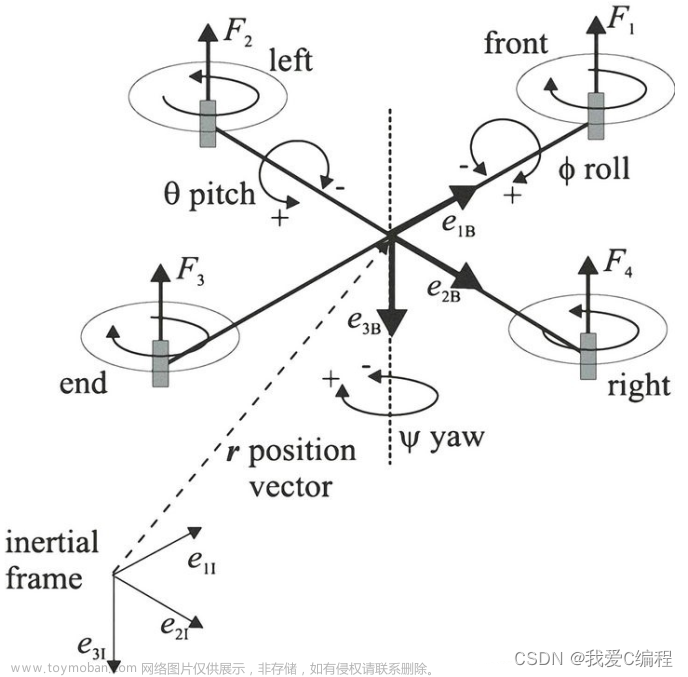
文件test/fault_AISMC.py实现了一个基于非线性动力学模型的无人机飞行控制仿真环境,通过使用自适应反演滑模控制器(Adaptive Inverse Sliding Mode Control,AdaptiveISMC_nonlinear)对无人机进行控制,并引入了执行器故障模型以模拟实际飞行中可能发生的故障情况。最后可视化仿真结果,展示了无人机在控制算法下的轨迹、执行器状态、故障检测与隔离等信息,用于分析控制器对飞行器动态响应及故障情况的影响。
文件test/fault_AISMC.py的具体实现流程如下所示。
(1)函数Env.init()用于初始化仿真环境,包括定义执行器故障(actuator_faults)、初始条件(ic)、参考轨迹(ref0)以及创建无人机模型(Copter_nonlinear)、执行器故障检测与隔离模块(FDI)和自适应反演滑模控制器(AdaptiveISMC_nonlinear)。
class Env(BaseEnv):
def __init__(self):
super().__init__(solver="odeint", max_t=20, dt=10, ode_step_len=100)
# Define faults
self.actuator_faults = [
LoE(time=5, index=0, level=0.0),
# LoE(time=10, index=3, level=0.3)
]
# Define initial condition and reference at t=0
ic = np.vstack((0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0))
ref0 = np.vstack((1, -1, -2, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0))
# Define agents
self.plant = Copter_nonlinear()
self.n = self.plant.mixer.B.shape[1]
self.fdi = FDI(numact=self.n)
self.controller = AdaptiveISMC_nonlinear(self.plant.J,
self.plant.m,
self.plant.g,
self.plant.d,
ic,
ref0)(2)函数Env.get_ref(t, x)的功能是根据当前时间 t 和状态 x 计算参考轨迹 ref,包括期望位置、速度、姿态和角速度。
def get_ref(self, t, x):
pos_des = np.vstack((1, -1, -2))
vel_des = np.vstack((0, 0, 0))
quat_des = np.vstack((1, 0, 0, 0))
omega_des = np.zeros((3, 1))
ref = np.vstack((pos_des, vel_des, quat_des, omega_des))
return ref(3)函数Env._get_derivs(t, x, p, gamma, effectiveness)的功能根据当前时间 t、状态 x、控制参数 p、滑模变量 gamma 和执行器效应性 effectiveness 计算执行器指令、执行器输出、作用在飞行器上的力和滑模变量。
def _get_derivs(self, t, x, p, gamma, effectiveness):
ref = self.get_ref(t, x)
forces, sliding = self.controller.get_FM(x, ref, p, gamma, t)
# Controller
Bf = self.plant.mixer.B * effectiveness
L = np.diag(effectiveness)
rotors_cmd = np.linalg.pinv(Bf.dot(L)).dot(forces)
rotors = np.clip(rotors_cmd, 0, self.plant.rotor_max)
return rotors_cmd, rotors, forces, ref, sliding(4)函数Env.set_dot(t的功能根据当前时间 t 更新仿真状态的导数,包括计算执行器指令、执行器输出和作用在飞行器上的力,并更新控制器和飞行器的状态。
def set_dot(self, t):
x = self.plant.state
p, gamma = self.controller.observe_list()
effectiveness = np.array([1.] * self.n)
for act_fault in self.actuator_faults:
effectiveness = act_fault.get_effectiveness(t, effectiveness)
rotors_cmd, rotors, forces, ref, sliding = \
self._get_derivs(t, x, p, gamma, effectiveness)
self.plant.set_dot(t, rotors)
self.controller.set_dot(x, ref, sliding)(5)函数Env.logger_callback(i, t, y, *args)是仿真过程中的日志记录回调函数,用于提取并返回包括时间 t、飞行器状态 x、执行器指令、执行器输出、参考轨迹、滑模变量和作用在飞行器上的力等信息的字典。
def logger_callback(self, i, t, y, *args):
states = self.observe_dict(y)
x_flat = self.plant.observe_vec(y[self.plant.flat_index])
ctrl_flat = self.controller.observe_list(y[self.controller.flat_index])
x = states["plant"]
effectiveness = np.array([1.] * self.n)
for act_fault in self.actuator_faults:
effectiveness = act_fault.get_effectiveness(t, effectiveness)
rotors_cmd, rotors, forces, ref, sliding = \
self._get_derivs(t, x_flat, ctrl_flat[0], ctrl_flat[1], effectiveness)
return dict(t=t, x=x, rotors=rotors, rotors_cmd=rotors_cmd,
ref=ref, gamma=ctrl_flat[1], forces=forces)(6)函数exp1_plot()用于绘制仿真结果的多个子图,包括飞行器执行器指令与实际输出的对比、期望轨迹与实际轨迹的对比、执行器故障检测与隔离滑模变量的演变,以及在执行器故障发生时的标注。通过可视化展示飞行器的动态响应和控制性能,有助于分析控制系统的稳定性和鲁棒性。
def exp1_plot():
data = fym.logging.load("case3_A.h5")
print(data.keys())
# Rotor
plt.figure()
ax = plt.subplot(411)
plt.plot(data["t"], data["rotors"][:, 0], "k-", label="Response")
plt.plot(data["t"], data["rotors_cmd"][:, 0], "r--", label="Command")
plt.ylim([-5.1, 45])
plt.legend()
plt.subplot(412, sharex=ax)
plt.plot(data["t"], data["rotors"][:, 1], "k-")
plt.plot(data["t"], data["rotors_cmd"][:, 1], "r--")
plt.ylim([-5.1, 45])
plt.subplot(413, sharex=ax)
plt.plot(data["t"], data["rotors"][:, 2], "k-")
plt.plot(data["t"], data["rotors_cmd"][:, 2], "r--")
plt.ylim([-5.1, 45])
plt.subplot(414, sharex=ax)
plt.plot(data["t"], data["rotors"][:, 3], "k-")
plt.plot(data["t"], data["rotors_cmd"][:, 3], "r--")
plt.ylim([-5.1, 45])
plt.gcf().supxlabel("Time, sec")
plt.gcf().supylabel("Rotor force")
plt.tight_layout()
plt.figure()
ax = plt.subplot(411)
plt.plot(data["t"], data["ref"][:, 0, 0], "r-", label="x (cmd)")
plt.plot(data["t"], data["x"]["pos"][:, 0, 0], label="x")
plt.plot(data["t"], data["ref"][:, 1, 0], "r--", label="y (cmd)")
plt.plot(data["t"], data["x"]["pos"][:, 1, 0], label="y")
plt.plot(data["t"], data["ref"][:, 2, 0], "r-.", label="z (cmd)")
plt.plot(data["t"], data["x"]["pos"][:, 2, 0], label="z")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(412, sharex=ax)
plt.plot(data["t"], data["x"]["vel"].squeeze())
plt.legend([r'$u$', r'$v$', r'$w$'], loc='center left', bbox_to_anchor=(1, 0.5))
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(413, sharex=ax)
plt.plot(data["t"], data["x"]["quat"].squeeze())
plt.legend([r'$q0$', r'$q1$', r'$q2$', r'$q3$'])
# plt.plot(data["t"], np.transpose(quat2angle(np.transpose(data["x"]["quat"].squeeze()))))
# plt.legend([r'$psi$', r'$theta$', r'$phi$'], loc='center left', bbox_to_anchor=(1, 0.5))
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(414, sharex=ax)
plt.plot(data["t"], data["x"]["omega"].squeeze())
plt.legend([r'$p$', r'$q$', r'$r$'], loc='center left', bbox_to_anchor=(1, 0.5))
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
# plt.xlabel("Time, sec")
# plt.ylabel("Position")
# plt.legend(loc="right")
plt.tight_layout()
plt.figure()
ax = plt.subplot(411)
plt.plot(data['t'], data['gamma'].squeeze()[:, 0])
plt.ylabel(r'$-\hat{h_{1}}$')
plt.grid(True)
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(412, sharex=ax)
plt.plot(data['t'], data['gamma'].squeeze()[:, 1])
plt.ylabel(r'$\hat{h_{2}}$')
plt.grid(True)
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(413, sharex=ax)
plt.plot(data['t'], data['gamma'].squeeze()[:, 2])
plt.ylabel(r'$\hat{h_{3}}$')
plt.grid(True)
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.subplot(414, sharex=ax)
plt.plot(data['t'], data['gamma'].squeeze()[:, 3])
plt.ylabel(r'$\hat{h_{4}}$')
plt.grid(True)
plt.axvspan(5, 5.042, alpha=0.2, color="b")
plt.axvline(5.042, alpha=0.8, color="b", linewidth=0.5)
plt.annotate("Rotor 0 fails", xy=(5, 0), xytext=(5.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=1.5))
plt.xlabel("Time [sec]")
plt.tight_layout()
# fig4 = plt.figure()
# ax1 = fig4.add_subplot(4, 1, 1)
# ax2 = fig4.add_subplot(4, 1, 2, sharex=ax1)
# ax3 = fig4.add_subplot(4, 1, 3, sharex=ax1)
# ax4 = fig4.add_subplot(4, 1, 4, sharex=ax1)
# ax1.plot(data['t'], data['forces'].squeeze()[:, 0])
# ax2.plot(data['t'], data['forces'].squeeze()[:, 1])
# ax3.plot(data['t'], data['forces'].squeeze()[:, 2])
# ax4.plot(data['t'], data['forces'].squeeze()[:, 3])
# ax1.set_ylabel('F')
# ax1.grid(True)
# ax2.set_ylabel('M1')
# ax2.grid(True)
# ax3.set_ylabel('M2')
# ax3.grid(True)
# ax4.set_ylabel('M3')
# ax4.grid(True)
# ax4.set_xlabel('Time [sec]')
# plt.tight_layout()
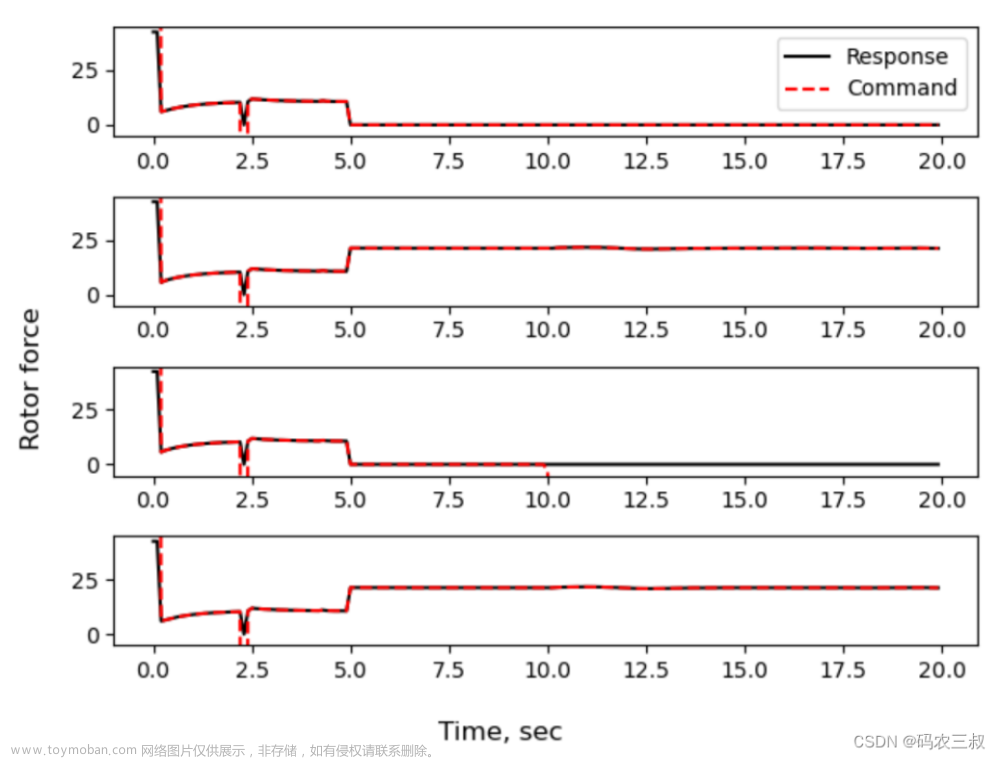
plt.show()执行后将回执多个子图,如图2-8所示。
- 执行器输出与指令对比图:包含四个子图,每个子图对应飞行器的一个执行器,展示了执行器的实际输出与控制器指令之间的对比,以评估执行器的性能。
- 控制系统状态与期望轨迹对比图:包含四个子图,分别展示了飞行器的位置、速度、姿态以及角速度的实际状态与期望轨迹之间的对比,以评估控制系统的跟踪性能。
- 执行器故障检测与隔离滑模变量演变图: 展示了执行器故障检测与隔离系统的滑模变量在时间上的演变,以分析故障检测与隔离性能。

 文章来源:https://www.toymoban.com/news/detail-853341.html
文章来源:https://www.toymoban.com/news/detail-853341.html
图2-9 绘制的子图文章来源地址https://www.toymoban.com/news/detail-853341.html
未完待续
到了这里,关于(2-3-3)位置控制算法:无人机运动控制系统——基于自适应反演滑模控制器的仿真测试的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!