讲清楚灰狼优化算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了讲清楚灰狼优化算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

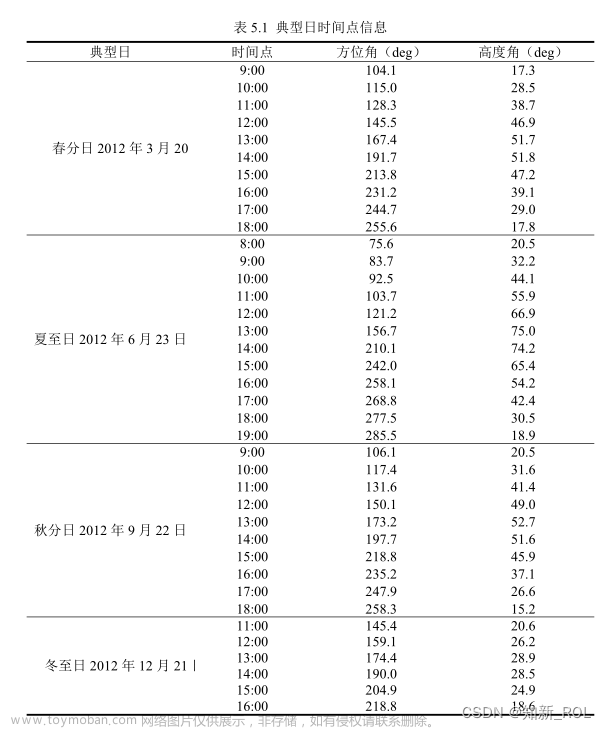
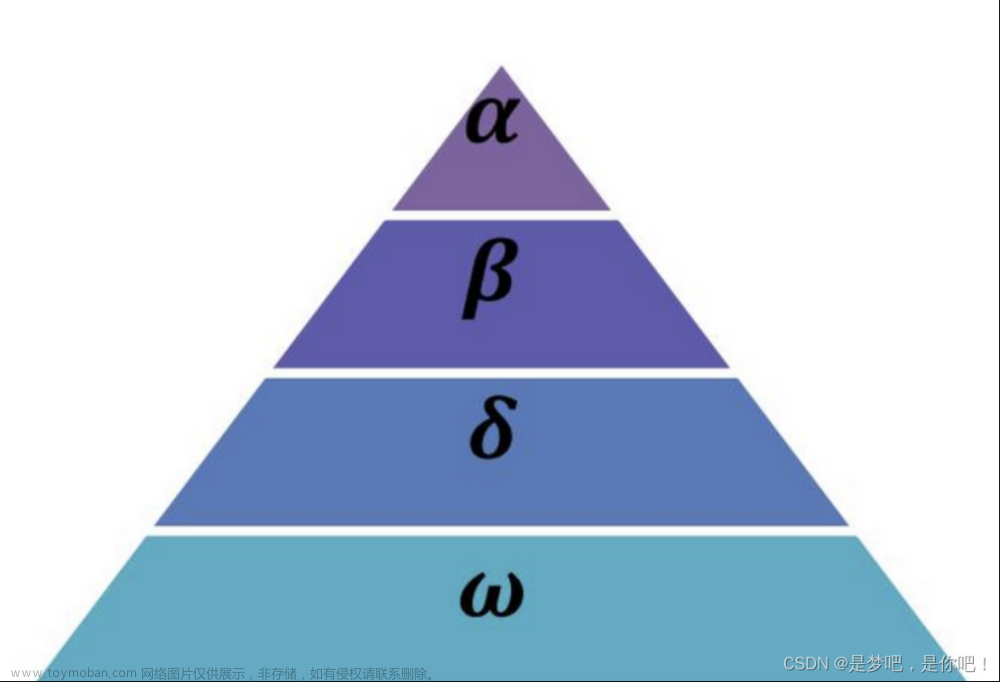
什么是灰狼优化算法

灰狼优化算法（Grey Wolf Optimizer, GWO）是一种模仿灰狼捕食行为的优化算法。它的数学建模原理基于灰狼的社会等级和捕猎策略。在这个算法中，灰狼群被分为四个等级：首领（Alpha, α）、副手（Beta, β）、侦察兵（Delta, δ）和欧米伽（Omega, ω）。算法通过模拟灰狼的社会合作行为来寻找最优解。下面是其数学建模原理的简化解释：

社会等级：在算法开始时，会随机生成一群灰狼（解的候选者），通过评估每个解的适应度来模拟社会等级，其中最好的解被认为是Alpha（α），第二和第三好的解分别是Beta（β）和Delta（δ）。其余的解则被视为Omega（ω）。这个社会结构帮助指导搜索过程，确保多样性和算法的收敛。
环绕、追踪和攻击猎物：灰狼的捕食行为被简化为数学模型，用以指导灰狼（解的搜索代理）向猎物（最优解）靠近。这个过程涉及到“环绕猎物”、“追踪猎物”和“攻击猎物”三个阶段。
- 环绕猎物：通过数学公式模拟灰狼环绕猎物的行为，公式会计算出灰狼应该在搜索空间中的位置，这个位置取决于当前的Alpha、Beta和Delta的位置。
- 追踪猎物：算法会根据猎物的动态位置更新灰狼的位置，以模拟追踪行为。
- 攻击猎物：当灰狼（搜索代理）足够接近最优解（猎物），算法会进行细微的调整，模拟攻击行为，以精确找到最优解。
- 更新位置：算法会根据Alpha、Beta和Delta的当前位置更新其他灰狼的位置。这个过程不断重复，直到满足停止条件（例如，达到最大迭代次数或达到足够好的解）。

数学上，灰狼的位置更新依赖于与Alpha、Beta和Delta之间的距离，这些距离会随机地调整，以模拟灰狼在捕猎时的接近和包围猎物的行为。整个过程旨在通过社会等级和集体行动的模拟，高效地探索解空间，并找到问题的最优解。

更新位置：算法会根据Alpha、Beta和Delta的当前位置更新其他灰狼的位置。这个过程不断重复，直到满足停止条件（例如，达到最大迭代次数或达到足够好的解）。

实际案例

我们来尝试一个更详细的步骤和计算过程，以便更好地理解灰狼优化算法（GWO）是如何工作的。我们会用同一个函数
$f(x)=x^2$ 我们将更详细地执行和解释每一步。

1.初始步骤

随机初始化位置：我们设定三只灰狼（Alpha、Beta、Delta）的初始位置，仍然使用
$X_{\alpha}=2,X_{\beta}=-1.5,X_{\delta}=0.5,$

2.第一轮迭代

为了简化，我们将按以下步骤进行一轮迭代，并提供具体的计算过程。

计算每只狼的适应度

$f(X_\alpha)=4$
$f(X_\beta)=2.25$
$f(X_\delta)=0.25$

因此，我们按适应度排名，Delta是目前的领头（因为我们是最小化问题，所以适应度最小的是领头），其次是Beta，Alpha是最后。

更新系数A和C
在实际情况下，
A和C 的值在每次迭代时都是动态计算的，但为了简化，假设我们得到
A=0.5和C=1.5。这些值通常由随机数生成和参数a计算得来。其中a从2线性减少到0.
更新系数

对于每只狼（假设这里只计算Alpha的新位置作为示例），位置更新依据是：
灰狼优化算法,大数据相关算法,算法,数学建模
这里，我们假设所有灰狼都向Delta（当前最佳位置）移动。实际上，Alpha、Beta和Delta的新位置会基于整个群体的当前最优三个位置进行更新，但为了简化，我们只展示了如何更新Alpha的位置。

在实际应用中，每一轮迭代中，所有灰狼的位置都会这样更新，随着迭代的进行，A和C 的动态变化引导着灰狼群体向全局最优解靠拢。对于多维优化问题，位置更新会在每一个维度上独立进行。

经过多轮迭代后，适应度函数在不断引导搜索过程，群里将逐渐聚集在最优解附近。

最后一轮迭代结束时，算法的输出通常包括以下几个方面：

最优解的位置：这是算法认为的最优解或近似最优解的位置。在我们的示例 $f(x)=x^2$ 中，最优解的位置理应是 $x = 0$ ，因为这个位置的函数值最小， $f (x) = 0$ .

最优解的函数值：这是在最优解位置处的函数值，代表了问题的最优目标值。对于最小化问题，这是所有迭代中找到的最小函数值；对于最大化问题，则是最大的函数值。在我们的案例中，最优解的函数值是 $f (0) = 0$
收敛历史：大多数优化算法，包括GWO，都会记录下每次迭代中最优解的变化情况，这有助于分析算法的收敛速度和行为。这可以是一个迭代次数与最优函数值的图表，显示随着迭代次数增加，函数值是如何变化的。

最优解的位置： $x \approx 0$ 一般这个值是我们要的。
最优解的函数值： $f (x) \approx 0$
收敛历史：显示了随着迭代次数增加，最优解的函数值逐渐降低并趋于稳定的过程。

代码复现-基于python

import numpy as np

# 目标函数：f(x) = x^2
def objective_function(x):
    return x ** 2

# 更新狼的位置
def update_position(alpha_pos, beta_pos, delta_pos, position, a, a_dim):
    A1 = 2 * a * np.random.rand(a_dim) - a
    C1 = 2 * np.random.rand(a_dim)
    D_alpha = abs(C1 * alpha_pos - position)
    X1 = alpha_pos - A1 * D_alpha
    
    A2 = 2 * a * np.random.rand(a_dim) - a
    C2 = 2 * np.random.rand(a_dim)
    D_beta = abs(C2 * beta_pos - position)
    X2 = beta_pos - A2 * D_beta
    
    A3 = 2 * a * np.random.rand(a_dim) - a
    C3 = 2 * np.random.rand(a_dim)
    D_delta = abs(C3 * delta_pos - position)
    X3 = delta_pos - A3 * D_delta
    
    new_position = (X1 + X2 + X3) / 3
    return new_position

# GWO算法
def grey_wolf_optimizer(search_agents_count, function, dim, max_iter):
    alpha_pos = np.zeros(dim)
    beta_pos = np.zeros(dim)
    delta_pos = np.zeros(dim)
    
    alpha_score = float("inf")
    beta_score = float("inf")
    delta_score = float("inf")
    
    positions = np.random.uniform(-10, 10, (search_agents_count, dim))
    
    for t in range(max_iter):
        for i in range(search_agents_count):
            # 计算当前狼的适应度
            fitness = function(positions[i])
            
            # 更新Alpha、Beta和Delta
            if fitness < alpha_score:
                alpha_score = fitness
                alpha_pos = positions[i].copy()
            elif fitness < beta_score:
                beta_score = fitness
                beta_pos = positions[i].copy()
            elif fitness < delta_score:
                delta_score = fitness
                delta_pos = positions[i].copy()
                
        a = 2 - t * (2 / max_iter)  # a从2线性减少到0
        
        for i in range(search_agents_count):
            positions[i] = update_position(alpha_pos, beta_pos, delta_pos, positions[i], a, dim)
    
    return alpha_pos, alpha_score

# 主程序
if __name__ == "__main__":
    search_agents_count = 10  # 狼群的数量
    max_iter = 20  # 最大迭代次数
    dim = 1  # 问题的维度
    
    best_pos, best_score = grey_wolf_optimizer(search_agents_count, objective_function, dim, max_iter)
    
    print(f"Best Position: {best_pos}, Best Score: {best_score}")

可视化

import numpy as np
import matplotlib.pyplot as plt

# 目标函数：f(x) = x^2
def objective_function(x):
    return x ** 2

# 更新狼的位置
def update_position(alpha_pos, beta_pos, delta_pos, position, a, a_dim):
    A1 = 2 * a * np.random.rand(a_dim) - a
    C1 = 2 * np.random.rand(a_dim)
    D_alpha = abs(C1 * alpha_pos - position)
    X1 = alpha_pos - A1 * D_alpha
    
    A2 = 2 * a * np.random.rand(a_dim) - a
    C2 = 2 * np.random.rand(a_dim)
    D_beta = abs(C2 * beta_pos - position)
    X2 = beta_pos - A2 * D_beta
    
    A3 = 2 * a * np.random.rand(a_dim) - a
    C3 = 2 * np.random.rand(a_dim)
    D_delta = abs(C3 * delta_pos - position)
    X3 = delta_pos - A3 * D_delta
    
    new_position = (X1 + X2 + X3) / 3
    return new_position

# GWO算法
def grey_wolf_optimizer(search_agents_count, function, dim, max_iter):
    alpha_pos = np.zeros(dim)
    beta_pos = np.zeros(dim)
    delta_pos = np.zeros(dim)
    
    alpha_score = float("inf")
    beta_score = float("inf")
    delta_score = float("inf")
    
    positions = np.random.uniform(-10, 10, (search_agents_count, dim))
    
    for t in range(max_iter):
        for i in range(search_agents_count):
            # 计算当前狼的适应度
            fitness = function(positions[i])
            
            # 更新Alpha、Beta和Delta
            if fitness < alpha_score:
                alpha_score = fitness
                alpha_pos = positions[i].copy()
            elif fitness < beta_score:
                beta_score = fitness
                beta_pos = positions[i].copy()
            elif fitness < delta_score:
                delta_score = fitness
                delta_pos = positions[i].copy()
                
        a = 2 - t * (2 / max_iter)  # a从2线性减少到0
        
        for i in range(search_agents_count):
            positions[i] = update_position(alpha_pos, beta_pos, delta_pos, positions[i], a, dim)
    
    return alpha_pos, alpha_score, positions

# 主程序
search_agents_count = 10  # 狼群的数量
max_iter = 20  # 最大迭代次数
dim = 1  # 问题的维度

best_pos, best_score, final_positions = grey_wolf_optimizer(search_agents_count, objective_function, dim, max_iter)

# 可视化
x = np.linspace(-10, 10, 400)
y = objective_function(x)

plt.figure(figsize=(10, 6))
plt.plot(x, y, label="Objective Function: $f(x) = x^2$")
plt.scatter(final_positions, objective_function(final_positions), color="red", label="Final Positions of Grey Wolves")
plt.scatter(best_pos, best_score, color="gold", marker="*", s=200, label="Best Position")
plt.title("Grey Wolf Optimizer (GWO) Finding Minimum of $f(x) = x^2$")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()

灰狼优化算法,大数据相关算法,算法,数学建模
从图中可以看出，灰狼的最终位置聚集在了函数的最低点附近，这表明GWO成功地引导了搜索过程向全局最小值逼近。这个简单的示例清楚地展示了GWO算法的工作原理和其在寻找最优解方面的能力。文章来源地址https://www.toymoban.com/news/detail-853858.html