1. 不同路径(62)
题目描述:
状态表示:
设dp[i][j]表示到达(i,j)位置时的路径数目。
状态转移方程:
dp[i][j]=dp[i-1][j]+dp[i][j-1]。这里分析起来很简单,因为这算是很经典的问题了。机器人只能向下或者向右走,所以到达(i,j)就有两种方式,分别是从(i-1,j)向下以及(i,j-1)向右,那么到达(i,j)位置的路径数只需要将到达(i-1,j)以及(i,j-1)位置的路径数相加即可。
初始化:
初始化就是为了避免越界问题,因为这里的状态转移方程涉及到i-1以及j-1。这里可以在矩阵外添加一行和一列,至于对于一行和一列的初始化要注意不能影响最终输出的结果,另外这样初始化还要注意下标的映射关系,这东西讲不清具体得看代码,这样初始化的好处就是可以将一整个矩阵全写进循环。
填表顺序:
从上到下,从左至右。
返回值:
因为添加了一行一列所以返回dp[m][n]。
代码如下:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)
2. 不同路径 II(63)
题目描述:
状态表示:
和上一题一样(i,j)位置的路径数为dp[i][j]。
状态转移方程:
实际上这题的状态转移方程也非常类似于上一题,但是要考虑一个特殊情况,就是障碍的情况。当(i,j)是障碍物的情况下直接将dp[i][j]=0,当(i,j)不是障碍物的情况下dp[i][j]=dp[i-1][j]+dp[i][j-1]。
初始化:
这里的初始化和上一题是一致的额,没什么好说的。。但是要提前判断左上角为障碍物的情况,直接返回0。
填表顺序:
从上往下,从左至右。
返回值:
与上题一致也是返回dp[m][n]。
代码如下:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
if (obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (obstacleGrid[i - 1][j - 1] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m][n];
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)
3. 珠宝的最高价值(LCR 166)
题目描述:
状态表示:
这题与上面两题也是相似的,只不过给出的矩阵多出了一个值的属性,说白了这篇博客就是将路径问题进行的一个分类总结。这题的状态表示根据经验和题目要求可以设置为dp[i][j]表示在(i,j)位置能够拿到的最大珠宝价值。
状态转移方程:
到达(i,j)位置还是只能够从(i-1,j)以及(i,j-1),因此要得到(i,j)位置的最大价值首先要将dp[i-1][j]与dp[i][j-1]的价值进行比较得到最大值赋给dp[i][j],状态转移方程为dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i][j]。
初始化:
还是类似加上一行和一列,但是这里不用做别的操作了,行和列赋0即可。但是还要注意dp数组与frame数组的映射关系。
填表顺序:
从上到下,从左至右。
返回值:
dp[m][n]。
代码如下:
class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length;
int n = frame[0].length;
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
}
}
return dp[m][n];
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)
4. 下降路径最小和(931)
题目描述:
状态表示:
根据经验加题目要求可以将dp[i][j]定义为到达(i,j)位置的最小路径和。
状态转移方程:
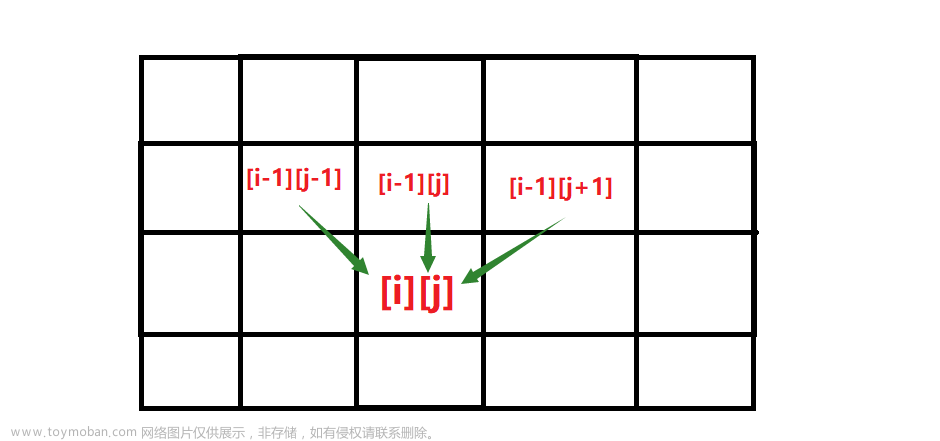
(i,j)上一行相邻的位置有(i-1,j)(i-1,j-1)(i-1,j+1),因此要求得到达(i,j)位置的最小路径和就可以列出以下状态转移方程,dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+ matrix[i][j]。
初始化:
要避免到达(i,j)位置的前三个位置越界可以在矩阵上加上左右两边的两列以及上边的一行,从而方便后续的操作,这里为了避免加上的空间影响最终得到的结果要注意把加上的一行赋值为0,加上的两列赋值为无穷大。
填表顺序:
从上到下,从左至右。
返回值:
要返回矩阵最后一行的最小值。
代码如下:
class Solution {
public int minFallingPathSum(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m + 1][n + 2];
for (int i = 0; i <= m; i++) {
dp[i][0] = Integer.MAX_VALUE;
}
for (int i = 0; i <= m; i++) {
dp[i][n + 1] = Integer.MAX_VALUE;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];
}
}
int min = Integer.MAX_VALUE;
for (int i = 1; i <= n; i++) {
if (min > dp[m][i]) {
min = dp[m][i];
}
}
return min;
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)
5. 最小路径和(64)
题目描述:
状态表示:
经验加题目要求,设定dp[i][j]表示到达(i,j)位置的最小路径和。
状态转移方程:
因为只能向下以及向右移动,所以dp[i][j]的值关联于dp[i-1][j]以及dp[i][j-1],即dp[i][j]=min(dp[i][j-1],dp[i-1][j])+grid[i][j]。
初始化:
也是一样为了避免越界,要给dp加上一行和一列的空间,这里要考虑到不能影响到最终的结果,因此除了左上角的左边和上边的空间其余空间都赋为无穷大。
填表顺序:
从上到下,从左至右。
返回值:
因为增加了一行和一列,所以应该返回dp[m][n]。
代码如下:
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i < n + 1; i++) {
dp[0][i] = Integer.MAX_VALUE;
}
for (int i = 0; i < m + 1; i++) {
dp[i][0] = Integer.MAX_VALUE;
}
dp[0][1] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
}
}
return dp[m][n];
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)
6. 地下城游戏(174)
题目描述:
状态表示:
根据经验以及题目要求这题定义dp[i][j]为以(i,j)为起点到达终点所需的最小点数。
状态转移方程:
根据经验与题目要求dp[i][j]定义为以位置(i,j)为起点营救公主所需的最低血量。因此位置(i,j)和其下边以及右边的dp元素的关系如下:
dp[i][j]+dungeon[i][j]>=dp[i+1][j]。
dp[i][j]+dungeon[i][j]>=dp[i][j+1]。
要满足以上条件,皆取最小值,即dp[i][j]=min(dp[i+1][j]-dungeon[i][j],dp[i][j+1]-dungeon[i][j]),不过要注意一个问题,当dungeon[i][j]的值是一个很大的值即一个很大的血包的时候,dp[i][j]就为负值了,要避免这种情况,如果出现血包很大的情况就将dp[i][j]直接赋为1即可,因为1就是逻辑上合理的最低血量。
初始化:
为了避免越界也要在dp上再多加一行和一列,这里的行和列是加在最后一行和最后一列。为了使添加之后不影响输出的结果,所以在行和列的每一个空间赋无穷大,只有右下角公主所在的位置的右边和下边赋为1,因为在逻辑上当营救完公主之后血量至少为1。
填表顺序:
从下到上,从右至左。
返回值:
dp[0][0]。
代码如下:文章来源:https://www.toymoban.com/news/detail-853881.html
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
dp[i][n] = Integer.MAX_VALUE;
}
for (int i = 0; i <= n; i++) {
dp[m][i] = Integer.MAX_VALUE;
}
dp[m][n - 1] = 1;
dp[m - 1][n] = 1;
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
dp[i][j] = Math.max(1, dp[i][j]);
}
}
return dp[0][0];
}
}
题目链接
时间复杂度:O(n^2)
空间复杂度:O(n^2)文章来源地址https://www.toymoban.com/news/detail-853881.html
到了这里,关于动态规划-路径问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!