【数据结构】【栈】括号匹配算法（可直接运行）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】【栈】括号匹配算法（可直接运行）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.算法问题

假设表达式中允许包含三种括号：()、[]、{}，其嵌套的顺序任意，即([]{})或[()[]{}]等均为正确的格式，实现一个算法，完成对表达式中括号的检验。

2.算法思路

考虑以下括号序列：
[ ( [ ] [ ] ) ]

分析如下：
（1）计算机接收第一个括号 [ 后，等待与之匹配的 ] 出现。
（2）接收第二个括号 ( 后，第一个括号放置一边，等待与之匹配的 ) 出现。
（3）接收第三个括号 [ 后，第二个括号暂时放置一边，等待能与之匹配的 ] 出现。
（4）直至第四个括号出现，发现其能与最近的第三个括号匹配，那第三个括号匹配完成，退出等待。
（5）以此类推，第五个等待，第六个与第五个匹配完成后，第五个退出等待；第七个与第二个匹配完成后，第二个退出等待；第八个与第一个匹配完成后，扫描完成，且等待序列中没有了数据，匹配成功。

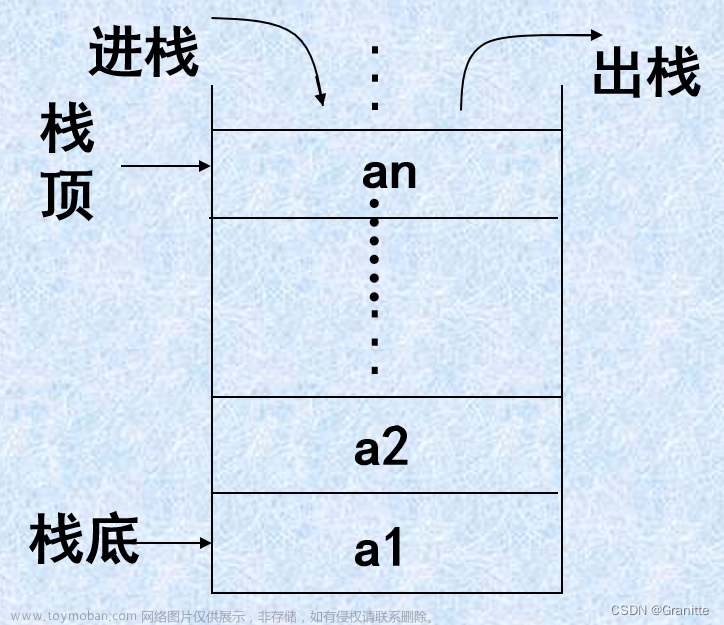
可以发现，此算法与栈的特性类似，后出现的左括号先匹配。

综上所述，可以得出大致算法如下：
（1）初始创立一个空栈。
（2）逐个读入括号。
（3）如果是左括号，那么就压入栈中。
（4）如果是右括号，则先检查栈是否为空，如果栈为空，则表示无左括号与之匹配，匹配失败。如果栈不为空，则进入下一步。
（5）从栈顶取出元素，检测此左括号与读入右括号是否匹配，如果不匹配，则返回匹配失败。如果匹配成功，则回到第二步，直至不满足循环条件。
（6）检测栈是否为空，如果栈为空，则表示匹配完成后还有多余的括号，匹配失败。若栈为空，则返回匹配成功。

3.算法实现

// 算法实现——括号匹配
bool bracketCheck(char str[], int length) {
    SeqStack S;
    // 初始化栈
    InitStack(S);
    // 通过遍历从左往右扫描字符
    for(int i = 0;i < length;i++) {
        // 如果字符是左括号，则压入栈中
        if(str[i] == '(' || str[i] == '[' || str[i] == '{') {
            Push(S, str[i]);
        } else {
            // 如果不是左括号，且栈为空则表示匹配失败
            // 因为栈中即是压入的左括号，如果匹配到右括号时，栈中没有左括号与之匹配，自然就不合理，匹配失败
            if(StackEmpty(S)) {
                return false;
            }
            // 创建临时变量，用于存储栈中所弹出的字符，即左括号
            char topElem;
            // 弹出栈顶元素
            Pop(S, topElem);
            // 如果括号类型不匹配，则视为匹配失败
            if(str[i] == ')' && topElem != '(') {
                return false;
            }
            if(str[i] == ']' && topElem != '[') {
                return false;
            }
            if(str[i] == '}' && topElem != '{') {
                return false;
            }
        }
    }
    // 检索完所有括号后，还需检测栈是否为空，如果栈不为空，说明还有未匹配完成项，即匹配失败
    // 栈空则匹配成功
    return StackEmpty(S);
}

4.完整代码

#include<stdio.h>

#define MaxSize 10

typedef struct {    // 定义顺序栈
    int data[MaxSize];  // 静态数组存放栈中元素
    int top;    // 栈顶指针：指向目前栈顶元素的位置
} SeqStack;

// 初始化
void InitStack(SeqStack &S) {
    // 初始化栈顶指针，由于在顺序栈中，0表示栈底部的位置
    // 所以初始应赋小于0的值，常用  -1
    S.top = -1;
}

// 判断栈空
bool StackEmpty(SeqStack S) {
    // 空栈条件：栈顶指针等于-1！！！
    // 说明栈中没有任何元素
    if(S.top == -1) {
        return true;
    } else {
        return false;
    }
}

// 进栈操作
// 类似于线性表的插入操作，即“增”操作
// 但由于栈的特殊性，只允许在栈顶进行操作，所以可称为进栈操作
// 即在栈顶增加元素
bool Push(SeqStack &S, char x) {
    // 判断栈是否已满，由于top是静态数组最后一个元素的下标（栈顶元素下标）
    // 所以只需要判断top值是否已经达到静态数组最大长度-1即可
    if(S.top == MaxSize - 1) {
        return false;
    }
    // top指针+1-->下标加一，指向数组后一位
    S.top = S.top + 1;
    // 新元素入栈
    S.data[S.top] = x;
    // 以上操作等价于S.data[++S.top] = x;
    return true;
}

// 出栈操作
// 类似于线性表的删除操作，即“删”操作
// 但由于栈的特殊性，只允许在栈顶进行操作，所以可称为出栈操作
// 即在栈顶弹出元素
bool Pop(SeqStack &S, char &x) {
    // 栈顶指针等于-1，栈为空，不可删除
    if(S.top == -1) {
        return false;
    }
    // 注意：虽然在此处出栈操作栈顶指针减一，可视为删除成功
    // 但实际上数据仍然保留在存储单元中，只是从逻辑上删除了
    // 将栈顶元素赋给x，x为引用变量，可从外部获取弹出的数据
    x = S.data[S.top];
    // 栈顶指针减一
    S.top = S.top - 1;
    // 以上操作等价于x= S.data[S.top--]
    return true;
}

// 算法实现——括号匹配
bool bracketCheck(char str[], int length) {
    SeqStack S;
    // 初始化栈
    InitStack(S);
    // 通过遍历从左往右扫描字符
    for(int i = 0;i < length;i++) {
        // 如果字符是左括号，则压入栈中
        if(str[i] == '(' || str[i] == '[' || str[i] == '{') {
            Push(S, str[i]);
        } else {
            // 如果不是左括号，且栈为空则表示匹配失败
            // 因为栈中即是压入的左括号，如果匹配到右括号时，栈中没有左括号与之匹配，自然就不合理，匹配失败
            if(StackEmpty(S)) {
                return false;
            }
            // 创建临时变量，用于存储栈中所弹出的字符，即左括号
            char topElem;
            // 弹出栈顶元素
            Pop(S, topElem);
            // 如果括号类型不匹配，则视为匹配失败
            if(str[i] == ')' && topElem != '(') {
                return false;
            }
            if(str[i] == ']' && topElem != '[') {
                return false;
            }
            if(str[i] == '}' && topElem != '{') {
                return false;
            }
        }
    }
    // 检索完所有括号后，还需检测栈是否为空，如果栈不为空，说明还有未匹配完成项，即匹配失败
    // 栈空则匹配成功
    return StackEmpty(S);
}

int main() {
    char a[] = "[([][])]";
    if(bracketCheck(a, 8)) {
        printf("The match is successful");
    }
}