title: 深入了解PBKDF2:密码学中的关键推导函数
date: 2024/4/20 20:37:35
updated: 2024/4/20 20:37:35
tags:
- 密码学
- 对称加密
- 哈希函数
- KDF
- PBKDF2
- 安全
- 密钥派生

第一章:密码学基础
对称加密和哈希函数
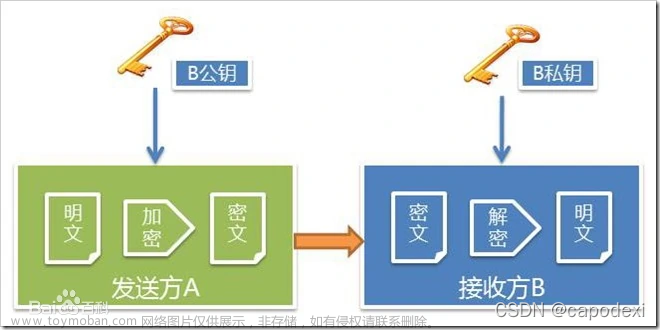
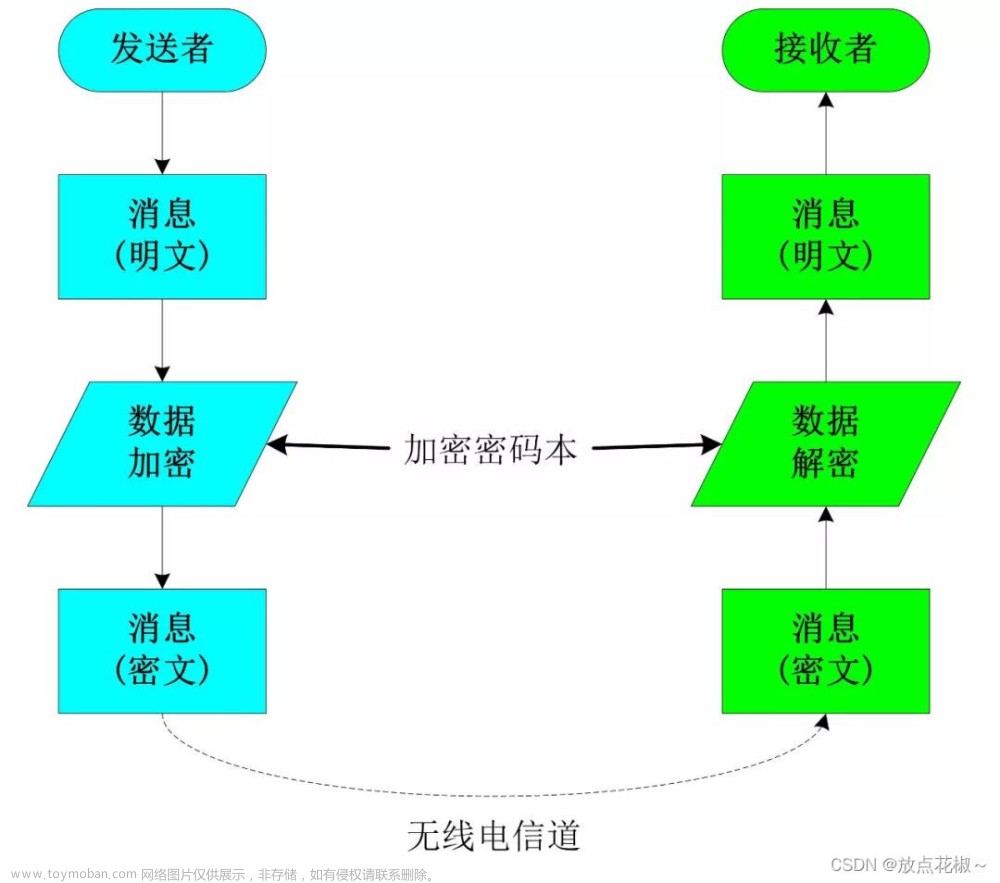
- 对称加密:对称加密是一种加密技术,使用相同的密钥进行加密和解密。常见的对称加密算法有AES、DES等。发送方和接收方必须共享相同的密钥才能进行加密和解密操作。
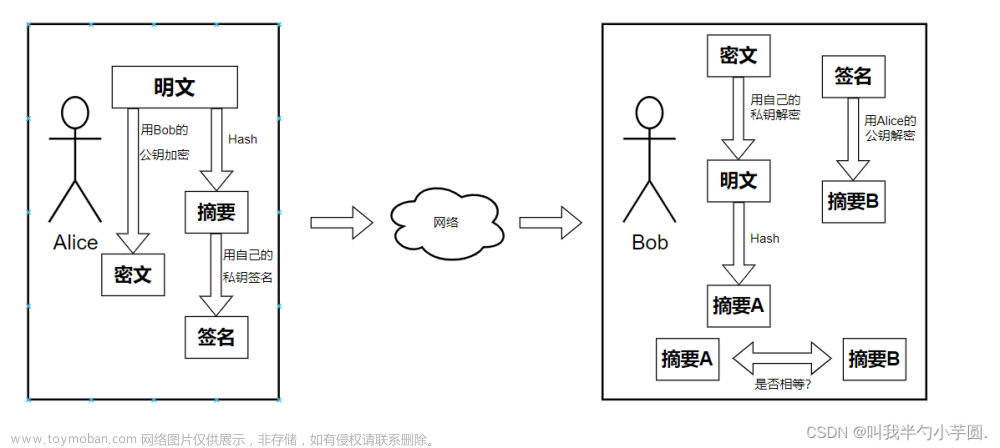
- 哈希函数:哈希函数是一种将任意长度的输入数据映射为固定长度输出的函数。哈希函数具有单向性、固定输出长度、雪崩效应等特性。常见的哈希函数有SHA-256、MD5等。哈希函数常用于数据完整性验证、密码存储等场景。
密钥派生函数的作用和原理
- 密钥派生函数:密钥派生函数(Key Derivation Function,KDF)是一种用于从一个或多个输入中派生出密钥或密钥材料的函数。其主要作用是从用户提供的密码和一些额外的参数中生成出更强大的密钥。
- 密钥派生函数的原理:密钥派生函数通常采用密码学哈希函数来实现。常见的密钥派生函数有PBKDF2、bcrypt、scrypt等。这些函数通常会使用盐值(salt)和迭代次数来增加生成密钥的难度,从而提高安全性。密钥派生函数的设计目的是为了抵抗暴力破解、字典攻击等密码破解手段,确保生成的密钥足够安全。
通过对称加密、哈希函数和密钥派生函数的基础理解,我们可以更好地理解密码学中的关键概念和技术,为后续学习和应用更复杂的密码学算法打下基础。
第二章:PBKDF2概述
PBKDF2的定义和特点
-
定义:PBKDF2(Password-Based Key Derivation Function 2)是一种基于密码的密钥派生函数,旨在从密码和盐值派生出加密密钥。PBKDF2使用可配置的伪随机函数(通常是HMAC)来执行多轮迭代,从而增加生成密钥的难度。
-
特点:
- 灵活性:PBKDF2支持不同的哈希函数和迭代次数,可以根据需要进行配置。
- 安全性:通过多轮迭代和盐值,PBKDF2增加了生成密钥的计算复杂度,提高了密码的安全性。
- 标准化:PBKDF2已被广泛应用于密码存储、密钥派生等领域,并且是一种标准化的密钥派生函数。
PBKDF2的应用场景和优势
-
应用场景:
- 密码存储:PBKDF2常用于将用户密码存储在数据库中。在用户登录时,系统可以使用PBKDF2重新计算密钥,并与存储的密钥进行比较以验证用户身份。
- 密钥派生:PBKDF2可用于从用户提供的密码中生成加密密钥,用于加密数据或通信。
- 安全协议:在安全协议中,PBKDF2可用于生成会话密钥、衍生密钥等。
-
优势:
- 抗暴力破解:PBKDF2通过多次迭代和盐值增加了生成密钥的难度,使得暴力破解更加困难。
- 灵活性:PBKDF2可以根据需要选择合适的哈希函数和迭代次数,适用于不同的安全需求。
- 标准化:作为一种标准化的密钥派生函数,PBKDF2得到了广泛的应用和支持。
通过了解PBKDF2的定义、特点、应用场景和优势,我们可以更好地理解如何使用PBKDF2来提高密码安全性、数据加密等方面的安全性。
第三章:PBKDF2的算法设计
PBKDF2的算法流程
- 输入:PBKDF2接受四个输入参数:密码(password)、盐值(salt)、迭代次数(iteration count)和所需的派生密钥长度(key length)。
- 伪随机函数:PBKDF2使用一个可配置的伪随机函数(通常是HMAC)来进行计算。
- 初始化:将密码和盐值连接起来,作为HMAC的输入。
- 迭代计算:PBKDF2通过多轮迭代计算派生密钥。每一轮迭代都会将上一轮的结果作为输入,并与密码、盐值和当前迭代次数一起传递给HMAC函数。
- 输出:最终得到的输出即为派生密钥。
PBKDF2中的盐值和迭代次数的作用
-
盐值(salt)的作用:
- 增加唯一性:盐值可以确保即使两个用户使用相同的密码,最终生成的密钥也是不同的,增加了唯一性。
- 抵抗彩虹表攻击:盐值使得预先计算的彩虹表无法直接应用于所有用户,提高了密码存储的安全性。
-
迭代次数的作用:
- 增加计算复杂度:通过增加迭代次数,PBKDF2需要更多的计算资源来生成密钥,增加了暴力破解的难度。
- 提高安全性:更多的迭代次数意味着更难以破解生成的密钥,从而提高了密码的安全性。
盐值和迭代次数的合理选择可以增加密码的安全性,防止常见的攻击方式,如暴力破解和彩虹表攻击。通过在PBKDF2中使用盐值和增加迭代次数,可以有效地提高密码的安全性。
第四章:PBKDF2的安全性分析
PBKDF2的抗攻击能力
PBKDF2具有以下抗攻击能力:
- 抵抗暴力破解:由于PBKDF2需要大量的计算资源来生成密钥,增加迭代次数可以有效防止暴力破解攻击。
- 抵抗彩虹表攻击:盐值和迭代次数的引入使得预先计算的彩虹表无法直接应用于所有用户,提高了抵抗彩虹表攻击的能力。
- 增加密码存储的安全性:盐值的使用确保即使两个用户使用相同的密码,最终生成的密钥也是不同的,提高了密码存储的安全性。
- 防止预计算攻击:PBKDF2中的迭代次数使得攻击者无法提前计算所有可能的密钥,增加了攻击的难度。
如何选择合适的盐值和迭代次数
-
盐值选择:
- 随机性:盐值应该是随机的,以确保每个用户的盐值都是独一无二的。
- 长度:盐值的长度应该足够长,通常推荐使用至少16字节的随机盐值。
-
迭代次数选择:
- 与计算资源成正比:迭代次数应该根据系统的计算资源来选择,以确保生成密钥的计算复杂度适中。
- 推荐值:通常推荐选择的迭代次数为至少1000次,具体的值可以根据系统的需求和性能进行调整。
综合考虑盐值和迭代次数的选择,可以提高PBKDF2的安全性。合适的盐值和迭代次数可以有效地增加生成密钥的计算复杂度,防止常见的密码攻击。
第五章:PBKDF2的实际应用
在密码存储中的应用
PBKDF2在密码存储中的应用通常涉及将用户密码转换为存储在数据库中的安全哈希值。以下是在密码存储中使用PBKDF2的一般步骤:
- 用户注册:当用户注册时,系统会生成一个随机的盐值,并结合用户输入的密码使用PBKDF2生成安全哈希值。
- 密码验证:当用户尝试登录时,系统会使用相同的盐值和迭代次数,结合用户输入的密码再次使用PBKDF2生成哈希值,并与数据库中存储的哈希值进行比较来验证密码的正确性。
在密钥派生中的应用
PBKDF2还可以用于从密码中派生密钥,用于加密通信或存储数据。以下是在密钥派生中使用PBKDF2的一般步骤:
- 生成密钥:系统使用PBKDF2函数,结合用户提供的密码和盐值,以及指定的迭代次数,生成足够强度的密钥。
- 加密通信:生成的密钥可以用于对通信数据进行加密,确保数据在传输过程中的安全性。
- 数据存储:生成的密钥也可以用于对数据进行加密,以确保数据在存储时的安全性。
在密钥派生中,PBKDF2的安全性和灵活性使其成为一种常用的方法,可以根据需要生成不同长度和强度的密钥,用于各种加密应用。
第六章:PBKDF2的性能优化
PBKDF2的性能优化策略
- 选择合适的哈希算法:PBKDF2可以使用不同的哈希算法作为基础,如SHA-1、SHA-256、SHA-512等。选择较快但仍安全的哈希算法可以提高性能。
- 适当选择迭代次数:迭代次数决定了PBKDF2的计算复杂度,过高的迭代次数会增加计算时间,但也提高了安全性。需要权衡安全性和性能,选择一个适当的迭代次数。
- 合理选择盐值长度:盐值的长度应足够长以保证其唯一性,但过长的盐值会增加计算开销。选择一个合适的盐值长度以平衡安全性和性能。
- 并行计算:PBKDF2的计算可以并行化,利用多核处理器或多线程可以提高计算速度。
- 缓存计算结果:对于相同的密码和盐值,可以缓存PBKDF2的计算结果,避免重复计算,提高性能。
如何平衡安全性和性能
- 选择合适的参数:在使用PBKDF2时,需要根据具体应用场景选择合适的哈希算法、迭代次数和盐值长度,以平衡安全性和性能要求。
- 定期评估安全性需求:随着计算机硬件的发展和密码学攻击技术的进步,安全性需求可能会发生变化。定期评估安全性需求,调整PBKDF2的参数以适应新的情况。
- 性能优化不应损害安全性:在进行性能优化时,不能牺牲安全性。确保任何优化措施都不会降低密码存储或密钥派生的安全性。
- 采用适当的加密方案:除了PBKDF2,还可以考虑其他密码学方案如bcrypt、scrypt等,它们可能在安全性和性能方面有不同的平衡点。
通过合理选择参数、优化计算过程以及定期评估安全性需求,可以在安全性和性能之间取得较好的平衡,确保系统既安全又高效。
第七章:PBKDF2的未来发展
PBKDF2的局限性和改进方向
- 固定迭代次数的弊端:PBKDF2使用固定的迭代次数,这导致其难以应对未来计算能力的提升和密码学攻击技术的发展。攻击者可以利用硬件加速或并行计算来降低PBKDF2的安全性。
- 不足的灵活性:PBKDF2的参数(如迭代次数、盐值长度)在使用过程中很难进行动态调整,这限制了它在不同场景下的适用性。
- 缺乏内置的并行计算支持:虽然PBKDF2的计算可以并行化,但其并没有内置对多核处理器或GPU的优化支持,这限制了其在高性能计算环境下的效率。
新兴的密钥派生函数及其对PBKDF2的影响
- Argon2:Argon2是一种新兴的密钥派生函数,被选为密码哈希竞赛(Password Hashing Competition)的胜出者。与PBKDF2相比,Argon2具有更高的安全性和灵活性,能够抵抗更广泛的攻击,并支持更灵活的参数设置。
- scrypt:scrypt是另一种密码哈希函数,与PBKDF2相比,它在抵御硬件加速攻击方面更有优势,因为其计算复杂度依赖于内存,而不仅仅是CPU。
- 影响:新兴的密钥派生函数的出现对PBKDF2提出了挑战,特别是在安全性和性能方面。这些新算法的出现推动了密码学领域的发展,也促使了对现有算法的评估和改进,以适应未来的需求。
未来,随着密码学领域的发展和安全性需求的不断提升,我们可能会看到更多针对PBKDF2局限性的改进和新的密钥派生函数的出现,以满足不同场景下的安全性和性能需求。在选择密钥派生函数时,需要综合考虑安全性、性能和灵活性等因素,以选择最适合特定应用场景的算法。
第八章:PBKDF2的案例分析
实际系统中PBKDF2的应用案例
- 密码存储:PBKDF2常用于加密存储用户密码。系统将用户密码与随机生成的盐值结合,经过PBKDF2计算生成密码哈希值,然后将哈希值与盐值一起存储在数据库中。这样即使数据库泄露,攻击者也难以通过简单的破解方法获取用户密码。
- 加密密钥派生:在加密通信或数据存储中,PBKDF2可以用于派生加密密钥。通过将用户提供的密码作为输入,结合盐值和适当的迭代次数,生成用于加密解密的密钥。
- 身份验证:一些系统在用户登录认证过程中使用PBKDF2来验证用户密码的正确性。系统会将用户输入的密码进行PBKDF2计算,然后与数据库中存储的密码哈希值进行比对,从而完成用户身份验证。
PBKDF2在密码学研究中的重要性
- 密码学安全性:PBKDF2是一种常用的密钥派生函数,对于提高密码学系统的安全性和抵御密码破解攻击至关重要。通过增加计算复杂度和盐值等机制,PBKDF2可以有效防止暴力破解和彩虹表攻击。
- 密码管理:在密码管理系统中,PBKDF2被广泛应用于加密存储和验证用户密码。它可以帮助系统管理员保护用户密码的安全,避免用户密码泄露导致的风险。
- 密码学研究:PBKDF2作为一种经典的密钥派生函数,在密码学研究中具有重要地位。通过对PBKDF2的分析和改进,研究人员可以不断提升密码学系统的安全性,推动密码学领域的发展。
总的来说,PBKDF2在实际系统中的应用案例丰富多样,涵盖了密码存储、加密通信、身份验证等多个领域。同时,作为密码学领域的重要组成部分,PBKDF2在密码学研究中扮演着关键的角色,对提高密码学系统的安全性和推动密码学领域的发展具有重要意义。
附录
在线PBKDF2计算工具
PBKDF2在线加密
https://amd794.com/pbkdf2
伪代码实现
以下是一个简单的伪代码示例,演示了如何使用PBKDF2函数生成密钥派生结果:
function PBKDF2(password, salt, iterations, key_length):
block_size = hash_function_output_size
iterations = max(iterations, 1)
key = ""
for i from 1 to ceil(key_length / block_size):
block = HMAC(password, salt + int_to_bytes(i))
intermediate_key = block
for j from 2 to iterations:
block = HMAC(password, block)
intermediate_key = intermediate_key XOR block
key = key + intermediate_key
return key[:key_length]
Python实现示例
以下是一个使用Python标准库中的hashlib模块实现PBKDF2的示例代码:文章来源:https://www.toymoban.com/news/detail-855180.html
import hashlib
import hmac
import struct
def pbkdf2(password, salt, iterations, key_length, hash_name='sha256'):
key = b''
block_size = hashlib.new(hash_name).digest_size
for i in range(1, (key_length // block_size) + 1):
block = hmac.new(password, salt + struct.pack('>I', i), hash_name).digest()
intermediate_key = block
for _ in range(2, iterations + 1):
block = hmac.new(password, block, hash_name).digest()
intermediate_key = bytes(a ^ b for a, b in zip(intermediate_key, block))
key += intermediate_key
return key[:key_length]
# 示例用法
password = b'password'
salt = b'salt'
iterations = 1000
key_length = 32
derived_key = pbkdf2(password, salt, iterations, key_length)
print(derived_key.hex())
在这个示例中,我们定义了一个pbkdf2函数,用于生成PBKDF2的密钥派生结果。然后我们提供了一个示例用法,展示了如何使用该函数生成密钥。您可以根据需要调整参数和哈希算法名称来适应您的实际应用场景。文章来源地址https://www.toymoban.com/news/detail-855180.html
到了这里,关于深入了解PBKDF2:密码学中的关键推导函数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!